Metoda Newtona-Raphsona - implementacje

Chcąc uzyskać pierwiastek kwadratowy z danej liczby najpewniej skorzystamy z funkcji sqrt() z biblioteki matematycznej i słusznie. Po co się kłopotać, gdy nie jest to konieczne. No, ale co jeśli będziemy pozbawieni możliwości użycia tej funkcji? No, tu zaczynają się schody… Trzeba wyznaczyć ten pierwiastek na własną rękę. Na pomoc przychodzi nam metoda Newtona-Raphsona, która jest jednym ze sposobów na wyznaczenie pierwiastka.

Metoda Newtona-Raphsona – teoretycznie

Metodą Newtona-Raphsona nazywamy algorytm iteracyjny, którego zadaniem jest wyznaczenie pierwiastka kwadratowego z liczby rzeczywistej. Wykorzystując jednak ten algorytm musimy wziąć pod uwagę fakt, iż wynik niekoniecznie musi być dokładny. Wpływają na to między innymi ograniczenia typów w kompilatorze.

Działanie metody opiera się na założeniu, że bok kwadratu o polu równym liczbie, dla której wyznaczamy pierwiastek, równa się się właśnie temu pierwiastkowi.

Przykład:

Dla przykładu spróbujemy wyznaczyć pierwiastek z liczby 36. Wiem, że dla człowieka to nie problem. Wystarczy sobie na szybciutko w głowie policzyć, że √36 to 6, ale komputer tego nie wie. Musimy mu pokazać jak do tego wyniku dojść.

Krok 1

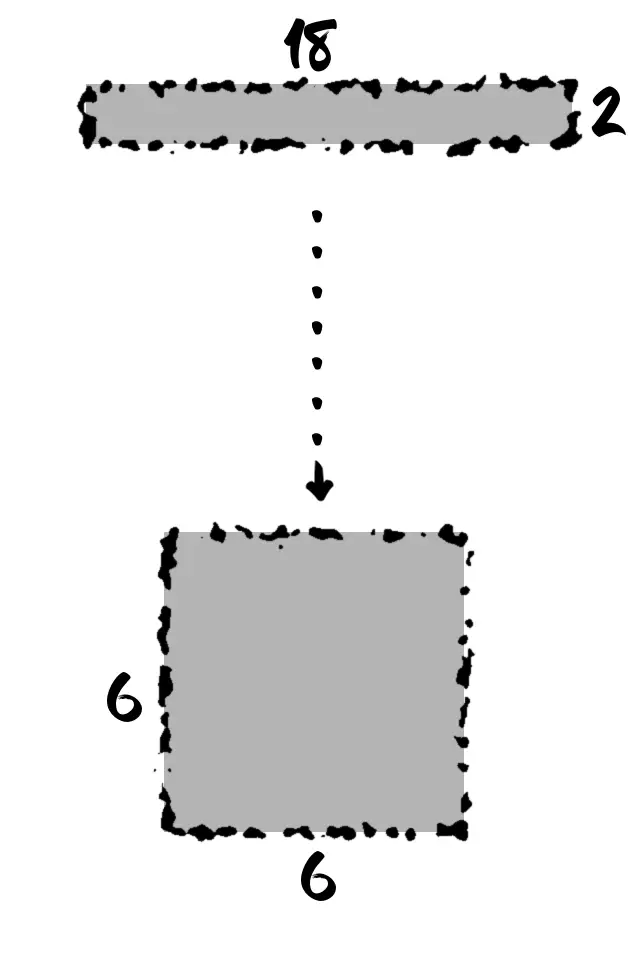
Długość pierwszego boku ustawiamy na długość równą połowie liczby 36, czyli 18, a drugi będzie się równał ilorazowi 36 przez nowopowstały bok, czyli przez 18. Drugi bok wyniesie 2. Jeśli długość pierwszego boku podniesiona do potęgi drugiej będzie równa 36 to długość tego boku jest naszym pierwiastkiem. Niestety 18*18 nie równa się 36, więc idziemy dalej.

Krok 2

Pierwszy bok tym razem będzie się równał połowie sumy dwóch poprzednich boków. (18+2)/2=10. Natomiast drugi bok tak samo jak poprzednim razem równy jest ilorazowi liczby 36 przez pierwszy bok, czyli w tym przypadku będzie to 3.6. Druga potęga liczby nie równa się 36, więc idziemy do kolejnego kroku.

Krok 3

Tutaj postępujemy tak samo jak w kroku drugim (będziemy tak robić do skutku). Pierwszy bok to (10+3.6)/2=6.8, natomiast drugi to 36/6.8=5.29412. 6.8*6.8!=36.

Krok 4

Pierwszy bok ->6.04706, drugi bok ->5.95331. Kwadrat pierwszego boku nie równa się 36.

Krok 5

Pierwszy bok ->6.00018, drugi bok ->5.99982. Kwadrat pierwszego boku nie równa się 36.

Krok 6

Pierwszy bok ->6, drugi bok ->6. Kwadrat pierwszego boku równa się 36. Koniec działania algorytmu. Wynikiem jest 6.

W przypadku, gdy pierwiastek z liczby jest niewymierny algorytm będzie pracować, dopóki wynik będzie spełniał założoną dokładność, a mianowicie dopóki wartość bezwzględna różnicy dwóch boków będzie liczbą większą od założonej dokładności.

O wielu innych, równie przydatnych algorytmach, przeczytasz w tej książce

Metoda Newtona-Raphsona – algorytm

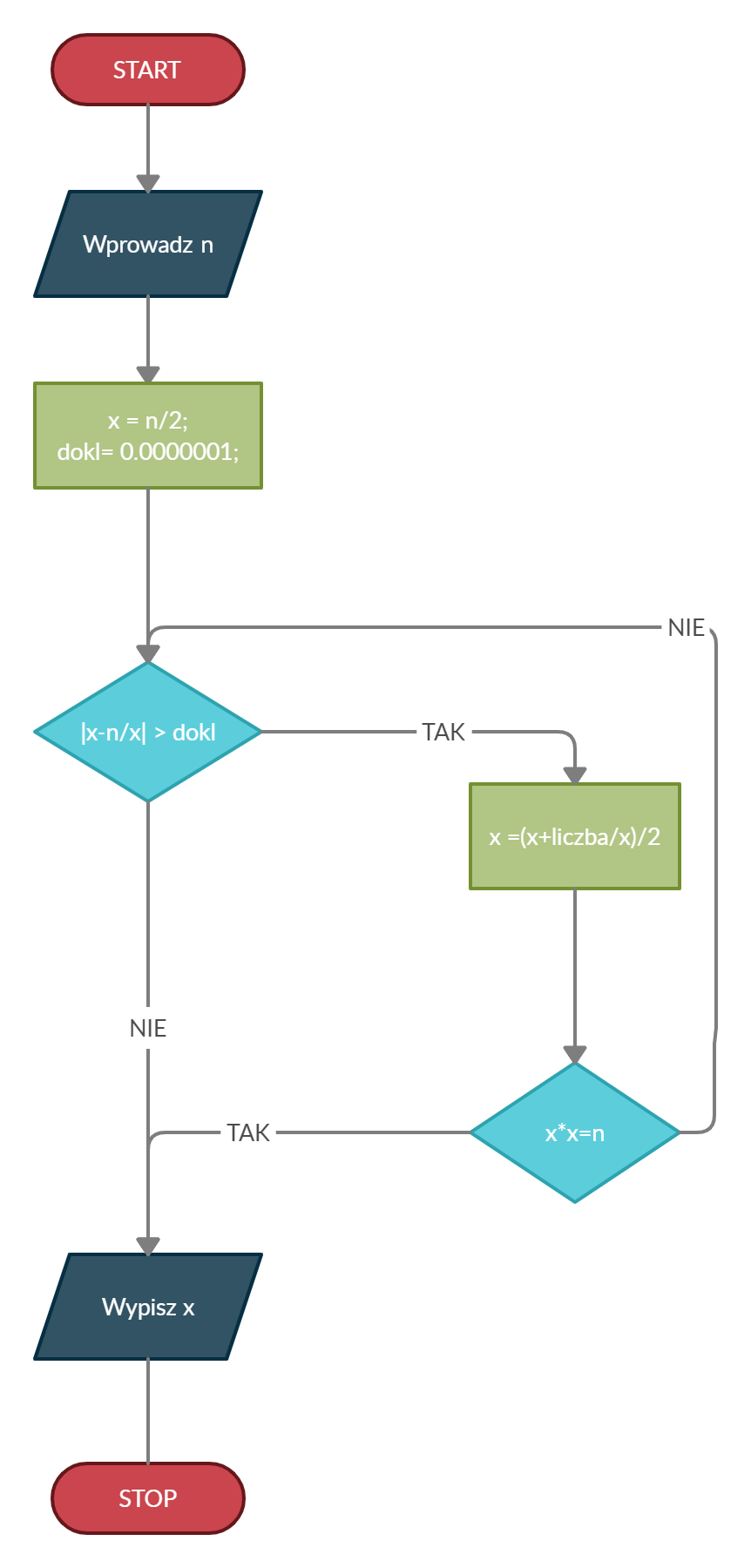
Tak wygląda nasz algorytm w postaci pseudokodu:

pobierz liczbę
x<-liczba/2
dopóki |x-liczba/x|> ustalona dokładność wykonuj
x=(x+liczba/x)/2
jeżeli x*x równa się liczbie zakończ działanie pętli

zwróć x

Tak zaś prezentuje się algorytm na schemacie blokowym:

metoda newtona-raphsona - schemat blokowy

Metoda Newtona-Raphsona implementacje

C++

//Program wyznaczający przybliżony pierwiastek kwadratowy z liczby rzeczywistej nieujemnej
//wykorzystujący w tym celu metodę Newtona-Raphsona
//Łukasz Kosiński
#include <iostream>
#include <cmath>

using namespace std;


double sqroot(double liczba)
{
	double x=liczba/2;
	while(fabs(x-liczba/x)>0.000001) 
    {
    	//cout << x << "|| " << liczba/x << endl;
    	//możemy odkomentować tą lnijkę żeby zobaczyć jak zmienia się nasz wynik
        x=(x+liczba/x)/2;//nową wartością boku jest średnia arytmetyczna dwóch poprzednich
	if(x*x==liczba) break;
    }
    return x;
}

int main()
{
	double dana;
	
	cin >> dana;
	
	cout << sqroot(dana);
	
	return 0;
}

//Program wyznaczający przybliżony pierwiastek kwadratowy z liczby rzeczywistej nieujemnej

//wykorzystujący w tym celu metodę Newtona-Raphsona

//Łukasz Kosiński

#include <iostream>

#include <cmath>

using namespace std;

double sqroot(double liczba)

{

double x=liczba/2;

while(fabs(x-liczba/x)>0.000001)

{

//cout << x << "|| " << liczba/x << endl;

//możemy odkomentować tą lnijkę żeby zobaczyć jak zmienia się nasz wynik

x=(x+liczba/x)/2;//nową wartością boku jest średnia arytmetyczna dwóch poprzednich

if(x*x==liczba) break;

}

return x;

}

int main()

{

double dana;

cin >> dana;

cout << sqroot(dana);

return 0;

}

Java

import java.util.Scanner;

public class Square_root {

	
	public static void main(String[] args) {
		System.out.println("Program liczący pierwiastek Metodą Newtona-Raphsona");
		System.out.println("Podaj liczbę do spierwiastkowania: ");
		Scanner scanner = new Scanner(System.in); // inicjalizacja skanera, który będzie pobierał wartości zmiennych
		float n = scanner.nextFloat(); // pobieramy liczbe przesuniec od uzytkownika
		
		System.out.println("Pierwiastek z liczby " + n + " jest równy: " + newton_raphson(n)); //drukujemy wynik
		scanner.close(); //zwalniamy zasoby
	}
	private static float newton_raphson(float n) { //tworzymy metodę obliczajaca pierwiastek
		float sec = n/2;
		while(Math.abs(sec-n/sec)> 0.00001f) {
			sec = (sec + n/sec)/2;
			if(sec*sec == n) break;
		}
		return sec;
	}
}

import java.util.Scanner;

public class Square_root {

public static void main(String[] args) {

System.out.println("Program liczący pierwiastek Metodą Newtona-Raphsona");

System.out.println("Podaj liczbę do spierwiastkowania: ");

Scanner scanner = new Scanner(System.in); // inicjalizacja skanera, który będzie pobierał wartości zmiennych

float n = scanner.nextFloat(); // pobieramy liczbe przesuniec od uzytkownika

System.out.println("Pierwiastek z liczby " + n + " jest równy: " + newton_raphson(n)); //drukujemy wynik

scanner.close(); //zwalniamy zasoby

}

private static float newton_raphson(float n) { //tworzymy metodę obliczajaca pierwiastek

float sec = n/2;

while(Math.abs(sec-n/sec)> 0.00001f) {

sec = (sec + n/sec)/2;

if(sec*sec == n) break;

}

return sec;

}

Python

import math


def sqrt(n): #definujemy oddzielna metode do liczenia pierwsiastka
    snd = n/2
    while math.fabs(snd - n/snd) > 0.000001:
        snd = float((snd + n/snd)/2)
        if snd*snd == n:
            break
    return round(snd, 6) #zaokraglamy liczbe do 6 miejsc po przecinku


print("Program liczący pierwiastek Metodą Newtona-Raphsona")
print("Podaj liczbę do spierwiastkowania: ")
num = float(input())
print("Pierwiastek z liczby " + str(num) + " = " + str(sqrt(num)))

import math

def sqrt(n): #definujemy oddzielna metode do liczenia pierwsiastka

snd = n/2

while math.fabs(snd - n/snd) > 0.000001:

snd = float((snd + n/snd)/2)

if snd*snd == n:

break

return round(snd, 6) #zaokraglamy liczbe do 6 miejsc po przecinku

print("Program liczący pierwiastek Metodą Newtona-Raphsona")

print("Podaj liczbę do spierwiastkowania: ")

num = float(input())

print("Pierwiastek z liczby " + str(num) + " = " + str(sqrt(num)))

Listę zagadnień, które mogą przydać Ci się na maturze, znajdziesz w tym wpisie.

Binarnie.pl

Metoda Newtona-Raphsona – implementacje