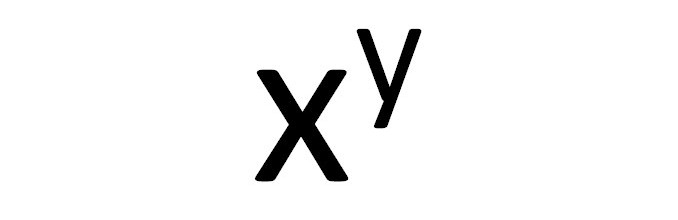Algorytmy stanowią podstawową część wiedzy wymaganej do matury z informatyki. Na łamach blogu udostępniłem cały szereg algorytmów, które na niej ci się przydadzą. Choć do części z nich dałoby radę dojść samemu, to i tak warto znać schemat ich działania, aby się nie pomylić. Jednym z algorytmów, które każdy powinien być w stanie napisać sam, jest potęgowanie.

Nie daj się zaskoczyć na maturze – zapisz się do listy mailingowej już teraz!
Pojęcie potęgowania powinno być znane każdemu z Was. Potęgę możemy zapisać jako an. Jest to, w uproszczeniu, n-krotne mnożenie liczby a*a. W uproszczeniu, ponieważ dotyczy to n całkowitego dodatniego. Dla n ujemnego potęgę możemy zapisać jako:
Jeżeli n będzie ułamkiem w postaci , to wtedy potęgę inaczej możemy zapisać jako:
Przy powyższych wzorach należy pamiętać, że jakakolwiek liczba podniesiona do potęgi 0 daje 1. Jeżeli ktoś poważnie myśli o dobrym wyniku z matury, to nie powinien mieć problemu ze stworzeniem rekurencyjnego algorytmu potęgowania. Niemniej jednak poniżej omówimy sobie, dla przypomnienia, jego schemat i implementacje.
Potęgowanie – algorytm
Na początku pobieramy dwie liczby: podstawę potęgi a i jej wykładnik n. Potęgowanie możemy wykonać na dwa sposoby: iteracyjny i rekurencyjny. W pierwszym sposobie tworzymy zmienną pomocnicza p=1.Potem wykonujemy n iteracji, gdzie w każdej z nich mnożymy p*a. My jednak posłużymy się sposobem rekurencyjnym, gdyż jest bardziej przejrzysty i równie wydajny co iteracyjny. Jeżeli nie wiesz czym jest rekurencja, zajrzyj do tego wpisu. W sposobie rekurencyjnym wykorzystamy zależność, że a^n = (a^(n-1)) * a. Ogółem wzór rekurencyjny możemy zapisać tak:
Nasz algorytm będzie wywoływać sam siebie, dzięki czemu otrzyma on wartości poszczególnych potęg o coraz to mniejszych wykładnikach. Będzie on wywoływać się, dopóki nie natrafi na warunek STOP – wykładnik równy 0. Wtedy to wszystkie wyniki wywołań zostaną wymnożone i zwrócone w głównym wywołaniu. Sposób ten możemy też wykorzystać dla wykładników ujemnych. Wystarczy w głównym wywołaniu funkcji zwrócić wartość 1/((a^(-n-2))* a). Powyższy algorytm przedstawiłem na poniższym schemacie blokowym:
Potęgowanie – implementacje
Skoro mamy już algorytm to, jak na każdy z algorytmów przystało, pora przejść do jego wdrożenia. Przygotowałem dla Was implementacje w trzech, popularnych językach: C++, Javie oraz Pythonie. Jeżeli przygotowujesz się do matury z informatyki, pewnie wiesz, że możesz na niej wybrać jeden z tych języków. Z tego też powodu opisałem każdy kod źródłowy, abyś mógł go lepiej zrozumieć, ale też i zapamiętać.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
//program obliczający potęgę danej liczby o wykładniku naturalnym //Kosiński Łukasz #include <iostream> using namespace std; long double potega(double podstawa, unsigned wykladnik) { if(wykladnik==0)return 1; else return podstawa*potega(podstawa, wykladnik-1); } int main() { double x; int y; do { cin >> x; cin >> y; cout << potega(x,y) << endl; }while(x!=0);//pętla bedzie się wykonywać dopóki nie wpiszemy zera system("pause"); return 0; } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
public class Potega { public static void main(String[] args) { System.out.println("Program liczący potęgi dwóch liczb. (a^n)"); System.out.println("Podaj podstawę potęgi (a): "); Scanner scanner = new Scanner(System.in); // inicjalizacja skanera, który będzie pobierał wartości zmiennych int a = scanner.nextInt(); System.out.println("Podaj wykładnik potęgi (n): "); int n = scanner.nextInt(); scanner.close(); // zwalniamy zasoby System.out.println("Liczba " + a + ", podniesiona do potęgi " + n + ", jest równa: " + power(a, n)); } private static float power(int a, int n) { // funkcja rekursywna if(n == 0) // jakakolwiek liczba do zerowej potęgi jest zawsze równa jeden return 1; if(n < 0) // jeżeli wykładnik potęgi jest ujemny, to tworzymy ułamek 1/(a^(-n)) return 1/(power(a, -n-1) * a); else // w przeciwnym wypadku po prostu liczymy potęgę o wykladniku o jeden mniejszym od n (rekurencja) i mnożymy ją przez a return power(a, n-1) * a; } } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
def power(a, b): #definiujemy rekurencyjna funkcje if b == 0: # jakakolwiek liczba do zerowej potęgi jest zawsze równa jeden return 1 if b < 0: # jeżeli wykładnik potęgi jest ujemny, to tworzymy ułamek 1/(a^(-n)) return 1/(power(a, -b-1) * a) else: # w przeciwnym wypadku po prostu liczymy potęgę o wykladniku o jeden mniejszym od n (rekurencja) i mnożymy ją przez a return power(a, b-1) * a print("Program liczacy potege x^y") print("Podaj liczbę x: ") x = int(input()) print("Podaj liczbę y: ") y = int(input()) print("Potega z tych liczb jest rowna " + str(power(x, y))) #wywolujemy funkcje od razu ja wypisujac |
Podsumowanie
Choć potęgowanie jest jednym z najbardziej podstawowych algorytmów, to jest jeszcze masa innych, tych bardziej skomplikowanych. Są one równie przydatne, zarówno na maturze, ale też i w codziennym programowaniu. Jeżeli więc chcesz się lepiej/więcej nauczyć, zajrzyj do tego wpisu. Znajdziesz tu również przydatne informacje na temat innych, ważnych zagadnień dotyczących matury z informatyki. Jeżeli chcesz wyrobić w sobie dobre nawyki w programowaniu, to powinieneś również rzucić okiem na ten tytuł: