Dawno się nie widzieliśmy! Właśnie z tego powodu przygotowałem dla Was kolejny wpis. Tym razem, nie podejmiemy się jednak tematu algorytmów sortowania, a kontynuować będziemy serię dotyczącą struktur danych. Zanim rozpoczniecie czytanie poniższego wpisu, zachęcam was do zapoznania się z poprzednimi częściami tej serii. Znajdziecie w nich opis stosu, listy jednokierunkowej oraz dwukierunkowej. W tych wpisach poznacie zagadnienia powiązane z podstawami struktur danych, które warto znać jako przyszły programista. Przejdźmy jednak do właściwej części tekstu, w której odpowiemy sobie na najważniejsze pytanie.
Czym jest drzewo?
Drzewo jako struktura danych, to grupa węzłów połączonych krawędziami. Węzeł początkowy, nazywany jest powszechnie korzeniem (root), a wierzchołki z których nie wychodzą żadne krawędzie, liśćmi (leafs). Każdy węzeł połączony z węzłem wyżej jest jego dzieckiem.
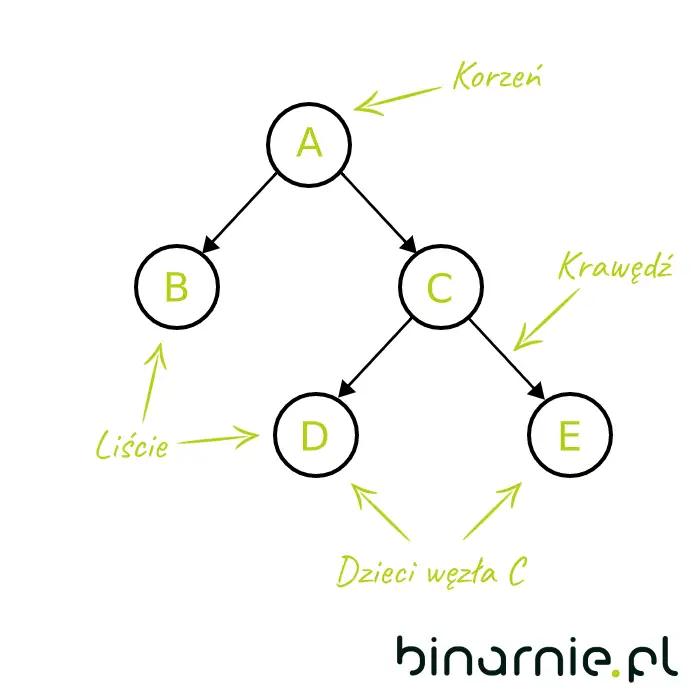
Jeżeli w drzewie każdy z węzłów ma maksymalnie dwoje dzieci, jest to drzewo binarne. W tym tekście omówimy sobie dokładniej BST (binary search tree) – podstawowy rodzaj drzewa binarnego.
BST, czyli binarne drzewo poszukiwań posiada jedną cechę charakterystyczną – po lewej stronie każdego poddrzewa znajdują się elementy mniejsze od wartości korzenia tego poddrzewa, a po prawej większe bądź równe. Może wydawać się to dość skomplikowane, lecz łatwo zrozumieć zasadę jego działania dzięki przykładowi.
BST – zasada działania
Weźmy drzewo, które posiada na początku tylko jeden węzeł (korzeń) o wartości 12. Chcąc dodać do tego drzewa nowy węzeł o wartości 5, przyrównujemy wartość nowego węzła do węzła początkowego. Jeśli będzie większa bądź równa idziemy na prawo, w przeciwnym wypadku idziemy na lewo. 5 jest mniejsze od 12, a co za tym idzie poruszamy się na lewo. Ze względu na to, że korzeń nie ma żadnych dzieci, lewa strona jest pusta. Oznacza to, że możemy wstawić w tym miejscu węzeł. Następnie wstawmy węzeł o wartości 33. Analogicznie poruszamy się w prawo, gdzie znajdziemy wolne miejsce na węzeł. Co należy jednak zrobić, gdy zechcemy w tym momencie wstawić do drzewa węzeł o wartości 7?
W pierwszym kroku przyrównujemy wartość nowego węzła do wartości korzenia. Ze względu na to, że wartość 7 jest mniejsza od 12, przechodzimy w lewo. Następnie przyrównujemy wartość 7 do wartości lewego dziecka korzenia, czyli 5. Wartość tego węzła jest mniejsza od wartości nowego, tak więc przechodzimy w prawo. Tam nie znajdziemy żadnego węzła, więc możemy wstawić w tym miejscu węzeł o wartości 7. Poniższa animacja pomoże wam zobrazować sobie ten przykład.

Podsumowując – gdy chcemy dodać jakikolwiek nowy węzeł staramy się znaleźć wolne miejsce, przechodząc w prawo, jeśli wartość nowego węzła jest większa bądź równa od aktualnie wskazywanego, lub w lewo, gdy jest mniejsza.
Drzewo BST – implementacja w C++
Nim zaprezentuję wam kod, należy poruszyć ważną kwestię. Według zasad drzewa BST, każdy z węzłów musi przechowywać przynajmniej: zmienną wartości węzła, wskaźnik na rodzica, wskaźnik na lewe dziecko i wskaźnik na prawe dziecko. Jeśli dany węzeł nie ma dziecka, po danej stronie, wskaźnik należy ustawić na wartość NULL. Dzięki temu, jesteśmy w stanie zweryfikować w prosty sposób czy dany wskaźnik wskazuje na dziecko, czy na pustą przestrzeń.
Poniższa implementacja posiada funkcje pozwalające na dodanie węzła, usunięcie węzła oraz znalezienie maksymalnej i minimalnej wartości w drzewie.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 |
//program do obslugi BST //Jan Żwirek #include <iostream> #include <fstream> #include <Windows.h> #include <string> using namespace std; struct node { int key; struct node *left; struct node *right; struct node *parent; }; //Wskaznik na korzen struct node *root = NULL; /* Funkcja dodawania wezla - funkcja ta przechodzi przez drzewo w poszukiwaniu wolnego miejsca na wezel. Jesli wartosc nowego wezla jest mniejsza od aktualnego, przechodzi w lewo, w przeciwnym przypadku przechodzimy w prawo. Gdy natkniemy sie na wartosc null wstawiamy tam nowy wezel pamietajac o przypisaniu wskaznikow. */ void add_node(int val) { //tworzymy wskazniki wskazujace na aktualnie rozpatrywany wezel i nowy wezel struct node *now = root; struct node *addedNode = new node; //Przypisujemy wartosci do wezla addedNode->key = val; addedNode->left = NULL; addedNode->right = NULL; //Jesli korzen ma wartosc null, nowy wezel staje sie korzeniem if (root == NULL) { addedNode->parent = NULL; root = addedNode; return; } else { while (now!= NULL) { //wartosc nowego wezla jest wieksza badz rowna od wskazywanego if (now->key <= addedNode->key) { //jesli po prawej jest wolne miejsce dodajemy w nie wezel if (now->right == NULL) { addedNode->parent = now; now->right = addedNode; return; } //w innym przypadku przechodzimy w glab drzewa else { now = now->right; } } //wartosc nowego wezla jest mniejsza od wskazywanego if (now->key > addedNode->key) { //jesli po lewej jest wolne miejsce dodajemy w nie wezel if (now->left == NULL) { addedNode->parent = now; now->left = addedNode; return; } //w innym przypadku przechodzimy w glab drzewa else { now = now->left; } } } } } /* Funkcja usuwania wezla - funkcja przechodzi po drzewie w poszukiwaniu wezla o zadanej wartosci. Jesli szukana wartosc jest mniejsza od wartosci aktualnie wskazywanego wezla, przechodzi w lewo, w przeciwnym przypadku przechodzimy w prawo. Jesli znajdziemy wezel o zadanej wartosci, usuwamy go. W przypadku gdy posiadal jakiekolwiek dzieci, wstawiamy je w wolne miejsce. Jesli zadana wartosc nie znajduje sie w drzewie, zwracamy NULL. */ struct node* del_node_key(struct node* node, int find) { if (node == NULL) return node; if (find < node->key) { return node->left = del_node_key(node->left, find); //Rekurencyjne przejście do szukanej wartości } else if (find > node->key) { return node->right = del_node_key(node->right, find); } if (find == node->key) { //Jeśli drzewo składa sie z samego korzenia if (root->left == NULL && root->right == NULL) { delete(root); root = NULL; return NULL; } //Wsunięcie prawego syna na miejsce aktualnie wskazywanego if (node->left == NULL) { struct node *tmp = node->right; delete(node); return tmp; } //Wsunięcie lewego syna na miejsce aktualnie wskazywanego else if (node->right == NULL) { struct node *tmp = node->left; delete(node); return tmp; } //Przypadek gdy wskazywany węzeł ma dwóch synów struct node* tmp = node->right; node->key = tmp->key; while (tmp->left != NULL) { tmp = tmp->left; } //Znalezienie następcy node->right = del_node_key(node->right, tmp->key); } return node; } //Szukanie najwiekszej wartosci w drzewie - skrajny prawy wezel int find_max() { struct node *now = root; //przejście do ostatniego elementu po prawej while (now->right != NULL) { now = now->right; } return now->key; } //Szukanie najmniejszej wartosci w drzewie - skrajny lewy wezel int find_min() { struct node *now = root; //przejście do ostatniego elementu po lewej while (now->left != NULL) { now = now->left; } return now->key; } int main() { bool isRunning = true; int answ, inpu; while (isRunning) { system("cls"); cout << endl; cout << "###########MENU###########" << endl; cout << "[1] Dodaj wezel" << endl; cout << "[2] Usun wezel" << endl; cout << "[3] Znajdz najmniejsza wartosc" << endl; cout << "[4] Znajdz najwieksza wartosc" << endl; cout << "[5] Wyjdz" << endl; cout << "##########################" << endl; cin >> answ; cout << endl; switch (answ) { case 1: { cout << "Wporwadz wartosc wezla: "; cin >> inpu; add_node(inpu); break; } case 2: { cout << "Wprowadz wartosc do usuniecia: "; cin >> inpu; if (root == NULL) { cout << "Brak korzenia - drzewo jest puste" << endl; } system("PAUSE"); break; } case 3: { cout << "Najmniejsza wartosc = " << find_min() << endl; system("PAUSE"); break; } case 4: { cout << "Najwieksza wartosc = " << find_max() << endl; system("PAUSE"); break; } case 5: { isRunning = false; break; } default: { cout << "Zly wybor!" << endl; system("PAUSE"); break; } } } return 0; } |
Podsumowanie
Drzewa (a zwłaszcza te binarne) to niezwykle popularny rodzaj struktury danych w informatyce. Drzewa ułatwiają i przyspieszają wyszukiwanie, a także pozwalają w łatwy sposób operować na posortowanych danych. Warto więc znać zasadę ich działania.





