Liczby pierwsze - omówienie i implementacje

Operacje na liczbach są jedną z podstawowych rzeczy, z jakimi możemy spotkać się w informatyce. W końcu każdy typ zmiennej jest przechowywany w pamięci jako ciąg zer i jedynek. Nic dziwnego więc, że na maturze z informatyki często pojawiają się zadania związane z liczbami i ich właściwościami — najczęściej ze zbioru liczb naturalnych. Ciekawymi przypadkami liczb naturalnych są liczby pierwsze.

Algorytm to podstawa

Aby dowiedzieć się, czy liczba n jest liczbą pierwszą, musimy stworzyć odpowiedni algorytm. Sprawdzimy najpierw, czy n jest większa od dwójki — jak wiemy z definicji liczby 0 oraz 1 nie są liczbami pierwszymi, więc od razu je wykluczamy. Następnie, korzystając z pętli, sprawdzimy wszystkie liczby mniejsze lub równe pierwiastkowi z liczby n, zaczynając od dwójki. Można by oczywiście iterować poprzez wszystkie liczby do n—1 lub n/2, jednakże sposób z pierwiastkiem jest wydajniejszy.

Do sprawdzania podzielności wykorzystamy operator modulo (%) — zwraca on resztę z dzielenia dwóch liczb. Jeżeli którakolwiek liczba z tego przedziału będzie dzielnikiem liczby n (reszta z dzielenia będzie równa 0), to zwracamy od razu FAŁSZ — nie ma potrzeby sprawdzać podzielności przez 1 i n, gdyż dobrze wiemy, że niezależnie od n zawsze będą one jej dzielnikami. Jeżeli jednak w wyniku iteracji nie znajdziemy żadnego dzielnika, oznacza to, że tylko te dwie liczby — 1 i n — są jej dzielnikami, więc jest ona liczbą pierwszą — zwracamy wtedy PRAWDĘ. Cały algorytm przedstawiłem na schemacie blokowym poniżej:

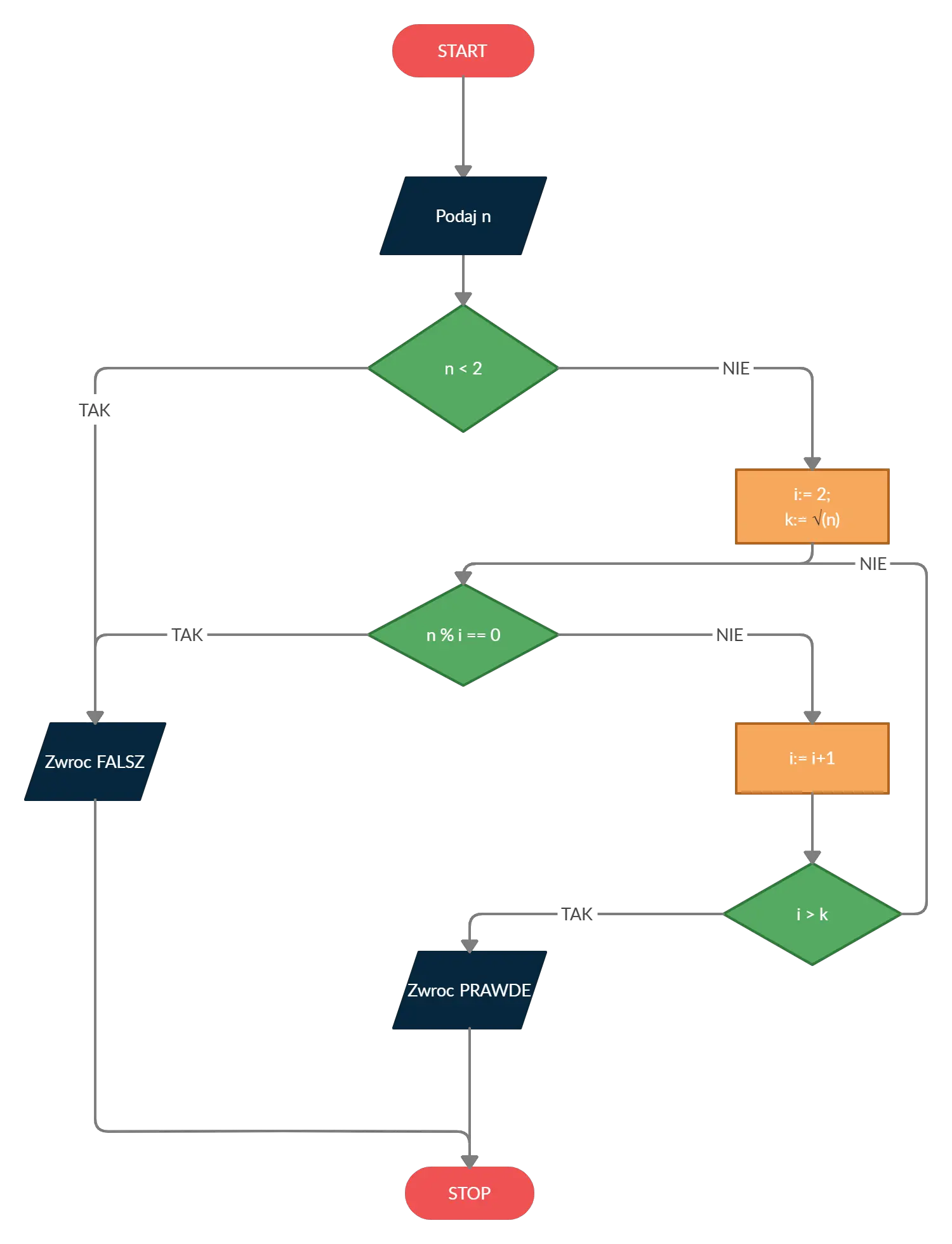
Liczby pierwsze — implementacja C++, Java, Python

Skoro mamy już algorytm, to pora go zastosować w wybranym języku. Na maturze z informatyki możesz wybrać jeden z trzech języków programowania, dlatego poniżej znajdziesz implementację w każdym z nich. Zwróć uwagę, że w C++ wykorzystaliśmy bibliotekę math.h, w Pythonie import math, zaś w Javie skorzystałem ze statycznej metody z klasy Math — wszystko to potrzebne, aby obliczyć pierwiastek kwadratowy (sqrt, z ang. square root) z liczby n.

Jeżeli chcesz poszerzyć swoją wiedzę na temat algorytmów, koniecznie sprawdź tę pozycję

Liczby pierwsze – implementacja C++

#include &lt;iostream>
#include &lt;math.h>

using namespace std;

bool sprawdz_czy_pierwsza(int a)
{
	if(a&lt;2) return false;//liczby pierwsze należą do przedziału [2,+8)
	//więc mniejszych od dwóch nie bierzemy pod uwagę
	
	for(int i=2; i&lt;=sqrt(a); i++)//wystarczy, że będziemy szukać dzielników do pierwiastka z liczby "a"
		if(a%i==0)return false;//jesli "i" jest dzielnikiem liczby "a" to "a" nie jest liczbą pierwszą
		
	return true;	
	
}


int main()
{
	int x;
	do
	{
	cin >> x;
	cout &lt;&lt; x &lt;&lt; " ";
	cout &lt;&lt; sprawdz_czy_pierwsza(x) &lt;&lt; endl;	
	} while(x!=0);//pętla bedzie się wykonywać dopóki nie wpiszemy zera
	
	
	return 0;
}

#include <iostream>

#include <math.h>

using namespace std;

bool sprawdz_czy_pierwsza(int a)

{

if(a<2) return false;//liczby pierwsze należą do przedziału [2,+8)

//więc mniejszych od dwóch nie bierzemy pod uwagę

for(int i=2; i<=sqrt(a); i++)//wystarczy, że będziemy szukać dzielników do pierwiastka z liczby "a"

if(a%i==0)return false;//jesli "i" jest dzielnikiem liczby "a" to "a" nie jest liczbą pierwszą

return true;

}

int main()

{

int x;

{

cin >> x;

cout << x << " ";

cout << sprawdz_czy_pierwsza(x) << endl;

} while(x!=0);//pętla bedzie się wykonywać dopóki nie wpiszemy zera

return 0;

}

Liczby pierwsze – implementacja Java

import java.util.Scanner;


public class Pierwsze {

	public static void main(String[] args) {
		Scanner n = new Scanner(System.in); // Pobieramy z konsoli liczbę którą chcemy sprawdzić
		int liczba = n.nextInt() ; //Scanner pobiera plik typu STRING dlatego używamy metody nextInt() do zamiany na liczbę całkowitą
		boolean pierwsza= true; //Zakładamy pierwotnie, że jest pierwszą
		for(int i=2; i&lt;Math.sqrt(n); i++){ //Sprawdzamy dla każdej liczby od 2 do pierwiastka z n, czy n jest podzielne przez nią
		if((liczba % i == 0)){
			pierwsza = false; //Jeśli liczbę możemy podzielić przez inną liczbę niż 1 i nią samą to NIE JEST LICZBA PIERWSZA
		}
		
		}
		if(pierwsza)System.out.println("Liczba " + liczba + " Jest liczbą pierwszą");
			else System.out.println("Liczba " + liczba + " Nie jest liczbą pierwszą");

	}

}

import java.util.Scanner;

public class Pierwsze {

public static void main(String[] args) {

Scanner n = new Scanner(System.in); // Pobieramy z konsoli liczbę którą chcemy sprawdzić

int liczba = n.nextInt() ; //Scanner pobiera plik typu STRING dlatego używamy metody nextInt() do zamiany na liczbę całkowitą

boolean pierwsza= true; //Zakładamy pierwotnie, że jest pierwszą

for(int i=2; i<Math.sqrt(n); i++){ //Sprawdzamy dla każdej liczby od 2 do pierwiastka z n, czy n jest podzielne przez nią

if((liczba % i == 0)){

pierwsza = false; //Jeśli liczbę możemy podzielić przez inną liczbę niż 1 i nią samą to NIE JEST LICZBA PIERWSZA

}

if(pierwsza)System.out.println("Liczba " + liczba + " Jest liczbą pierwszą");

else System.out.println("Liczba " + liczba + " Nie jest liczbą pierwszą");

}

Liczby pierwsze – implementacja Python

import math
def czyPierwsza(a):
    if a &lt; 2:
        return False
    for i in (range(2, int(math.sqrt(a)))):
        if a % i == 0:
            return False
    return True

print("Program sprawdzający, czy liczba jest liczbą pierwszą.")
print("Podaj liczbę: ")
a = int(input())
print(czyPierwsza(a))

import math

def czyPierwsza(a):

if a < 2:

return False

for i in (range(2, int(math.sqrt(a)))):

if a % i == 0:

return False

return True

print("Program sprawdzający, czy liczba jest liczbą pierwszą.")

print("Podaj liczbę: ")

a = int(input())

print(czyPierwsza(a))

Liczby pierwsze — ciekawostki

Liczb pierwszych jest nieskończenie wiele
Do tej pory nikt nie wyznaczył wzoru funkcji, która dla dowolnego argumentu zwróci liczbę pierwszą.
Liczby pierwsze występują, wydawać by się mogło, w sposób losowy — raz gęściej, raz rzadziej.
Badaniem liczb pierwszych zajmowali się m.in. Leonard Euler i Bernhard Riemann, którego twierdzenie jest uznawane za klucz do zrozumienia liczb pierwszych.
Istnieje algorytm, który znajdzie wszystkie liczby pierwsze z przedziału <2, n> dla n należącego do liczb naturalnych — jest to tzw. sito Eratostenesa, któremu poświęciłem oddzielny artykuł o tutaj.
Istnieje również algorytm rozkładu dowolnej liczby naturalnej na liczby pierwsze, który opisałem w tym artykule.

Na koniec warto dodać, że powyższy algorytm, jest jednym z wielu wymaganych przez CKE algorytmów na maturze z informatyki. Jeżeli więc pragniesz się do niej jak najlepiej przygotować, gorąco polecam Ci przeczytać ten post. Dowiesz się w nim na co należy zwrócić szczególną uwagę przy nauce, a także znajdziesz tam listę najważniejszych algorytmów, które mogą przytrafić się na egzaminie.

8 komentarzy

Ten od poddatkow
says:
18 września, 2021 at 19:13

Bardzo przydatne

Odpowiedz
Jednooki
says:
20 kwietnia, 2017 at 20:58

Nie do końca zrozumiałem powyższy kod i z innego źródła wziąłem trochę kodu i skleiłem coś takiego(zdjęcie kodu w załączniku). Jeśli nikomu to nie będzie przeszkadzało proszę o wytłumaczenie jak działa pętla for w napisanej funkcji.

Jeśli dobrze rozumiem. Dla przykładu zadeklarowaną przez użytkownika liczbą będzie 5(int n). Petlą wykonuje się następująco. Ona zaczyna pracować od 2, ponieważ jest to najmniejsza liczba pierwsza oraz będzie się wykonywać do jej kwadratu jeśli dobrze rozumiem z jej zapisu.
W instrukcji tej pętli mamy „n mod i” == 0. Czyli jeśli pętla zaczyna pracować przy podanym wyżej przykładzie to zaczyna dzielić podaną 5 przez 2 i zwraca nam prawdę ponieważ mamy resztę z dzielenia.

Chyba dobrze to rozumiem?

Jeszcze chcę się dowiedzieć, ponieważ w tej pętli mamy inkrementacje „i++”, która będzie nam zwiększała zmienną i po pozytywnym wykonaniu pętli. I chciałbym żeby ktoś mi to zobrazował w jaki to sposób działa jeśli przechodzi nam liczba początkowa i=2 na np. 3, ponieważ nie mogę sobie tego jakoś wyobrazić. Chyba że po prostu tak się nie będzie dało ponieważ to szuka nam czy liczba jest podzielna i jak nie jest zwraca nam prawdę…
https://uploads.disquscdn.com/images/fc2099ea7427f577783cbf1800fc764c55c765df65ed18b800362e9c15e560e8.png
Mam nadzieję, że ktoś zrozumie to co napisałem :DDD

Odpowiedz
- Łukasz Kosiński
  says:
  22 kwietnia, 2017 at 19:19
  
  Własnie nie mój drogi. Warunek 5%2==0 nie zwróci nam prawdy, gdyż wynikiem działania 5 mod 2 jest jeden (reszta z dzielenia dwójki przez pięć to właśnie jedynka), a jeden jest różne od zera, więc mamy fałsz także instrukcja return się nie wywoła.
  
  Dla takiej na przykład piątki funkcja sprawdzi najpierw, czy pięć jest podzielne przez dwa. Nie jest więc przejdzie do następnego kroku zwiększając przy okazji i (i++). Teraz „i” wynosi 3, ale i*i, czyli 3*3 jest większe od naszego n, czyli pięć także pętla kończy swoje działanie.
  
  Zadaniem funkcji sprawdz_czy_pierwsza jest sprawdzenie, czy liczba jest podzielna przez jakąkolwiek liczbę (poza jedynką i nią samą).
  Gdybyś tak miał na przykład sprawdzić, czy 25 jest liczbą pierwszą to funkcja działa tak… Najpierw sprawdza, czy 25 jest mniejsze od dwóch nie jest więc lecimy dalej. Zaczyna działać pętla. W pierwszej iteracji sprawdza, czy 25 jest podzielne przez 2. Nie jest więc zwiększamy i o 1 i sprawdzamy, czy 25 jest podzielne przez 3. Nie jest, więc znowu zwiększamy o 1. Mamy 4, które również dzieli 25 z resztą. Zwiększamy „i” o jeden, wynosi więc teraz 5. Sprawdzamy, czy jeszcze mieścimy się w warunku. 5*5=25, czyli warunek w pętli spełniony. Sprawdzamy, czy co powie nam if. 25%5==0 (?) TAK, ponieważ resztą z dzielenia 25 przez 5 jest 0. Także wykona nam się instrukcja return, która zwróci oczywiście fałsz -> liczba nie jest pierwsza.
  Taka rada ode mnie. Zawsze, gdy nie rozumiesz dlaczego coś nie działa (albo działa) sprawdź sobie działania pętli tak jakby krok po kroku. Wybierz sobie jakąś liczbę i wyobraź sobie jak wyglądałoby wykonanie funkcji dla niej.
  Pozdrawiam 😉
  
  Odpowiedz
gum
says:
27 marca, 2017 at 19:17

Może coś o liczbach w względnie pierwszych coś byś zrobił?

Odpowiedz
- adminkozaczek
  says:
  27 marca, 2017 at 19:49
  
  Dzięki, dopisałem do checklisty 🙂
  
  Odpowiedz
Gumix 69 here
says:
27 marca, 2017 at 19:08

Przydało by się kilka wersji programu żeby młodego programisty nie wpędzać od razu na morze rekurencji i do zatok wskaźników.

Odpowiedz
- adminkozaczek
  says:
  27 marca, 2017 at 19:51
  
  Wychodzę z założenia, że kursów programowania w internecie jest mnóstwo, dlatego nie chcę pisac żadnych tutoriali jak. Przedstawiam tylko możliwie optymalne rozwiązania., ale faktycznie może iteracyjna wersja też by się przydała 🙂
  
  Odpowiedz
Gumix 69 here
says:
27 marca, 2017 at 19:04

Ciekawie szybko i w skrócie.

Odpowiedz

Binarnie.pl

Liczby pierwsze – omówienie i implementacje

Algorytm to podstawa

Liczby pierwsze — implementacja C++, Java, Python

Liczby pierwsze – implementacja C++

Liczby pierwsze – implementacja Java

Liczby pierwsze – implementacja Python

Liczby pierwsze — ciekawostki

You Might Also Like

Jak wyjść z Vim

Praktyki w Scythe Studio

Praca zdalna jako junior

8 komentarzy

Ten od poddatkow

Jednooki

Łukasz Kosiński

gum

adminkozaczek

Gumix 69 here

adminkozaczek

Gumix 69 here

Dodaj komentarz Anuluj pisanie odpowiedzi