Sito Eratostenesa - algorytm i jego implementacje

W poprzednich wpisach omówiliśmy sobie czym są liczby pierwsze, a także jak rozłożyć dowolną liczbę na czynniki. Są to algorytmy, które bez wątpienia warto znać na maturze z informatyki. Kolejnym, równie ważnym algorytmem jest sito Eratostenesa.

Sito Eratostenesa to algorytm za pomocą, którego jesteśmy w stanie w szybki sposób wyznaczyć liczby pierwsze z przedziału od 2 do n, gdzie n jest górną granicą przedziału. Stworzenie algorytmu przypisuje się Grekowi, Eratostenosowi z Cyreny.

Sito Eratostenesa – działanie

Działanie algorytmu jest bardzo proste. Pobieramy najpierw liczbę n od użytkownika. Następnie tworzymy tablicę n-elementową, indeksowaną od 2 (bo to najmniejsza spośród liczb pierwszych), a następnie wartość każdej komórki w tablicy ustawiamy na prawdę. Bierzemy najmniejszy indeks (czyli dwa) i ustawiamy wartości wszystkich komórek, których indeksy są wielokrotnościami dwójki na fałsz. W dalszej kolejności postępujemy tak z następnym niewykreślonym indeksem, czyli trójką i analogicznie jak w przypadku dwójki ustawiamy wartości komórek o indeksach równych k*3 na fałsz.

W ten sposób postępujemy, dopóki obierany indeks będzie mniejszy lub równy pierwiastkowi z n. Dlaczego tak? Dlaczego do pierwiastka z n? Wynika to z tego, że liczba ma tyle samo dzielników mniejszych od tego pierwiastka, co większych od niego.

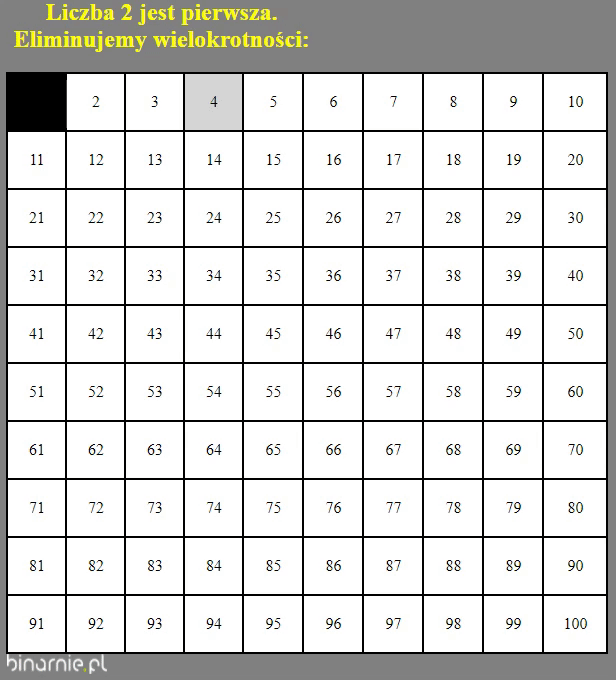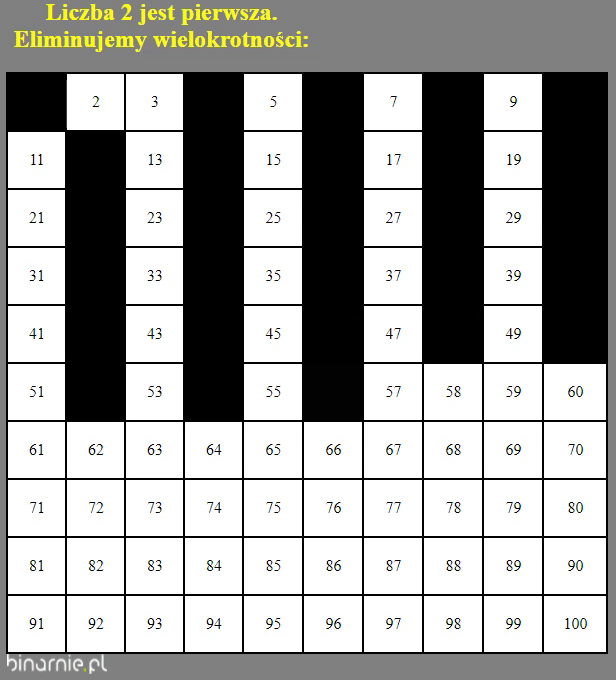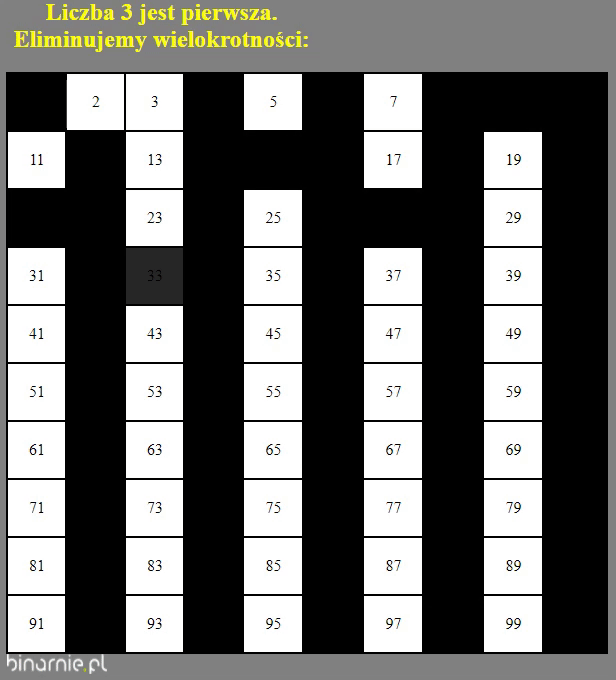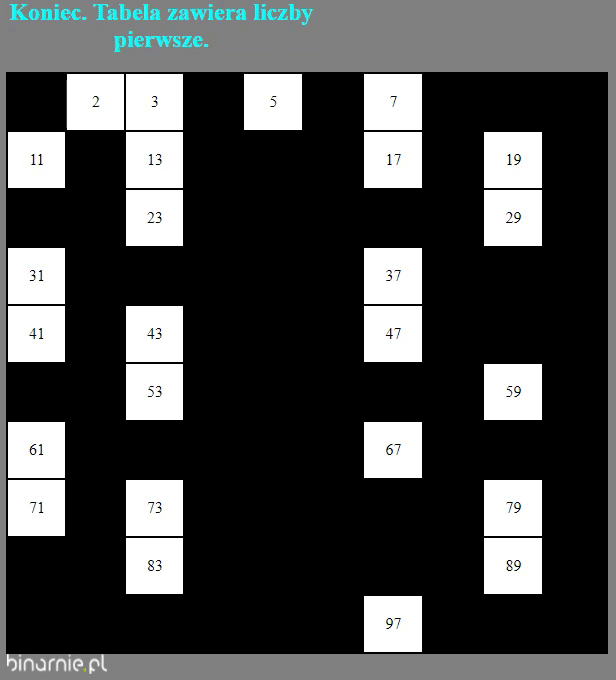
Spójrzmy na powyższy gif. Przedstawia on wyznaczanie liczb pierwszych z zakresu [2,100]. Jak widać proces, jaki zachodzi, w dużej mierze przypomina przesiewanie. Stąd nazwa – sito Eratostenesa. Starożytni Grecy to mieli mózgi. Taki Eratostenes na przykład… Człowiek orkiestra. Poeta, filozof, matematyk, geograf, astronom, piekarz, garncarz, tancerz…

Sito Eratostenesa – implementacje

Zastanawiać was może jakie zastosowanie może mieć ten algorytm? Przecież można by przeiterować poprzez wszystkie liczby, a następnie każdą z osobna sprawdzić. Sito Eratostenesa jest jednak szybsze i wydajniejsze. Może się przecież zdarzyć, że na maturze pojawi się wymóg, aby program był jak najbardziej optymalny.

A propos matury. Z racji, iż większość z Was się do niej właśnie uczy, przygotowałem poniżej trzy implementacje programu: w C++, Javie oraz Pythonie. Wszystko opisane komentarzami, aby wiadomo było o co biega:

C++

//program wyznaczający liczby pierwsze w danym przedziale z wykorzystaniem sita Eratostenesa
//Łukasz Kosiński
#include &lt;iostream>
#include &lt;cmath>
 
using namespace std;
 
void sito(int n)
{
	bool *tablica=new bool[n+1];
	
	for(int i=2; i&lt;=n; i++) tablica[i]=true;//wypełniamy tablicę wartościami logicznymi true
	
	
	for(int i=2; i&lt;=sqrt(n); i++)
	{
		if(tablica[i]==true)
			for(int j=i*i; j&lt;=n; j+=i) tablica[j]=false;//jeśli indeks jest wielokrotnością innego indeksu to ustawiamy jego wartośćna fałsz
	}
	
	
	cout &lt;&lt; "Liczby pierwsze, nalezace do przedzialu [2," &lt;&lt; n &lt;&lt; "] to: " &lt;&lt; endl;
	
	for(int i=2; i&lt;=n; i++)
	{
		if(tablica[i]==true) cout &lt;&lt; i &lt;&lt; endl;
	}
	
	
	delete [] tablica;
}
 
int main()
{
	
	int x;
	cout &lt;&lt; "Podaj interesujacy Cie zakres ";
	cin >> x;
	
	sito(x);
	
	return 0;
}

//program wyznaczający liczby pierwsze w danym przedziale z wykorzystaniem sita Eratostenesa

//Łukasz Kosiński

#include <iostream>

#include <cmath>

using namespace std;

void sito(int n)

{

bool *tablica=new bool[n+1];

for(int i=2; i<=n; i++) tablica[i]=true;//wypełniamy tablicę wartościami logicznymi true

for(int i=2; i<=sqrt(n); i++)

{

if(tablica[i]==true)

for(int j=i*i; j<=n; j+=i) tablica[j]=false;//jeśli indeks jest wielokrotnością innego indeksu to ustawiamy jego wartośćna fałsz

}

cout << "Liczby pierwsze, nalezace do przedzialu [2," << n << "] to: " << endl;

for(int i=2; i<=n; i++)

{

if(tablica[i]==true) cout << i << endl;

}

delete [] tablica;

}

int main()

{

int x;

cout << "Podaj interesujacy Cie zakres ";

cin >> x;

sito(x);

return 0;

}

Java

import java.util.Scanner;
public class Szukaj_Liczb_Pierwszych {

	public static void main(String[] args) {
		System.out.println("Program znajdujacy liczby pierwsze z przedzialu &lt;2,n>.");
		System.out.println("Podaj liczbę a: ");
		Scanner scanner = new Scanner(System.in); // inicjalizacja skanera, który będzie pobierał wartości zmiennych
		int n = scanner.nextInt(); //Pobieramy liczbę n dla której będziemy sprawdzać liczby pierwsze
		
		boolean[] liczby = new boolean[n+1]; // tworzymy tablice skladajacej się z n elementów
		for(int i = 2; i &lt;= n; i++) {
			liczby[i] = true; // kazdemu z nich nastepnie przypisujemy wartosc true
		}
		for (int i = 2; i &lt; Math.sqrt(n); i++) {
			if(liczby[i] == true) // nastepnie, zaczynajac od dwojki, eliminujemy wielokrotnosci liczb pierwszych przypisujac im wartosc false
				for(int k = i*i; k &lt;= n; k+=i)
					liczby[k] = false;
		}
		System.out.println("Liczby pierwsze z przedzialu &lt;2," + n + "> : ");
		for(int i = 0; i &lt;= n; i++)
		{
			if(liczby[i] == true)
				System.out.print(i + " | "); // wypisujemy znalezione liczby
		}
		scanner.close(); // zwalniamy zasoby
	}

}

import java.util.Scanner;

public class Szukaj_Liczb_Pierwszych {

public static void main(String[] args) {

System.out.println("Program znajdujacy liczby pierwsze z przedzialu <2,n>.");

System.out.println("Podaj liczbę a: ");

Scanner scanner = new Scanner(System.in); // inicjalizacja skanera, który będzie pobierał wartości zmiennych

int n = scanner.nextInt(); //Pobieramy liczbę n dla której będziemy sprawdzać liczby pierwsze

boolean[] liczby = new boolean[n+1]; // tworzymy tablice skladajacej się z n elementów

for(int i = 2; i <= n; i++) {

liczby[i] = true; // kazdemu z nich nastepnie przypisujemy wartosc true

}

for (int i = 2; i < Math.sqrt(n); i++) {

if(liczby[i] == true) // nastepnie, zaczynajac od dwojki, eliminujemy wielokrotnosci liczb pierwszych przypisujac im wartosc false

for(int k = i*i; k <= n; k+=i)

liczby[k] = false;

}

System.out.println("Liczby pierwsze z przedzialu <2," + n + "> : ");

for(int i = 0; i <= n; i++)

{

if(liczby[i] == true)

System.out.print(i + " | "); // wypisujemy znalezione liczby

}

scanner.close(); // zwalniamy zasoby

}

Python

import math #importujemy biblioteke potrzebna do pierwiastkowania i jego zaokgraglania


print("Program znajdujacy liczby pierwsze z przedzialu &lt;2,n>.")
print("Podaj liczbę n: ")
n = int(input())
liczby = [True] * (n+1) #tworzymy n+1 elementowa tablice
for i in range(2, int(math.ceil(math.sqrt(n)))): #iterujemy poprzez nia, zaczynajac od 2, a konczac na zaokraglonym do gory pierwiastkiem z n
    if liczby[i]: #jezeli liczba jest pierwsza
        for k in range(i*i, n+1, i): #oznacz wszystkie jej wielokrotnosci jako liczby zlozone
            liczby[k] = False
print("Liczby pierwsze z przedzialu &lt;2," + str(n) + "> : ")
for i in range(2, n+1): #wypisujemy elementy utworzonej tablicy
    if liczby[i]:
        print(str(i), end=" | ")

import math #importujemy biblioteke potrzebna do pierwiastkowania i jego zaokgraglania

print("Program znajdujacy liczby pierwsze z przedzialu <2,n>.")

print("Podaj liczbę n: ")

n = int(input())

liczby = [True] * (n+1) #tworzymy n+1 elementowa tablice

for i in range(2, int(math.ceil(math.sqrt(n)))): #iterujemy poprzez nia, zaczynajac od 2, a konczac na zaokraglonym do gory pierwiastkiem z n

if liczby[i]: #jezeli liczba jest pierwsza

for k in range(i*i, n+1, i): #oznacz wszystkie jej wielokrotnosci jako liczby zlozone

liczby[k] = False

print("Liczby pierwsze z przedzialu <2," + str(n) + "> : ")

for i in range(2, n+1): #wypisujemy elementy utworzonej tablicy

if liczby[i]:

print(str(i), end=" | ")

Sito Eratostenesa – co warto wiedzieć?

Algorytm ten powstał już w III wieku p.n.e. Eratostenes wychodził z założenia, że łatwiej jest mnożyć niż dzielić, w związku z czym przedstawił swój sposób.
Przy użyciu Sita Eratostenesa uczeni w XIX wieku wyznaczyli wszystkie liczby pierwsze do liczby 10000000. Wynik ich pracy przedstawił w swoim dziele Norman Lehmer.
Istnieje algorytm, który sprawdzi czy podana liczba jest pierwsza. Znajdziesz go w tym wpisie.
Istnieje również algorytm, który rozłoży dowolną liczbę na iloczyn liczb pierwszych. Przeczytasz o tym tutaj.

Podsumowanie

Sito Eratostenesa jest jednym z wielu algorytmów, które mogą przydać się na maturze z informatyki. Jeżeli chcesz więc zrobić powtórkę lub nauczyć się czegoś nowego, zajrzyj do tego wpisu.

5 komentarzy

Michał
says:
15 marca, 2022 at 21:12

Rozwiązanie w JAVIE (innych nie sprawdzałem), jest niepoprawne. Podajcie sobie np. liczbę 25 jako koniec przedziału. W wyniku też otrzymacie 25, mimo ze nie jest liczbą pierwszą.

Odpowiedz
Hailon
says:
6 kwietnia, 2019 at 21:38

Witam!
Czy da się stworzyć ten algorytm oparty na obiekcie „vector”?
Próbowałem wiele razy, najpierw uzupełniając liczbami naturalnymi obiekt vector rozpoczynając od 2, a następnie odejmując z całego zbieru liczb te, które nie są pierwsze.
Innym razem stworzyłem pusty obiekt vector i dodawałem do niego tylko liczby pierwsze.
Za każdym razem problem był z tym, że po każdym usunięciu lub dodaniu liczby do obiektu vector, zmieniała się jego wartość początkowa co powodowało, że przy wielokrotnościach 2, 3, 5 i 7 program usuwał niewłasciwą wartość.
Jeśli istnieje jakiś sposób na wykonanie tego algorytmu za pomocą vectora to proszę o porady 😉

Odpowiedz
Krzysztof
says:
17 lipca, 2017 at 08:47

Jest inny sposób poszukiwania liczb pierwszych też oparty na eliminacji. W Excelu można stworzyć tabelkę z liczbami naturalnymi. Pierwsza kolumna i pierwszy wiersz to dane wejściowe dla funkcji obliczającej dane w pozostałych komórkach tabeli exel. Funkcja generuje liczby złożone nigdy liczby pierwsze. Tak utworzoną tabela jest podstawą algorytmu (napisanego jako makro w exelu) o ilości iteracji pierwiastek z (×-c) dzielony przez 3 (gdzie c to reszta dzielenia z przez 3). Dodatkowo algorytm daje informację o rozmieszczeniu liczb pierwszych wokół liczby x. Zaletą algorytmu jest 100% identyfikacja liczby pierwszej oraz możliwość realizacji podziału obliczeń (tzw. rozproszone przetwarzanie). W tej chwili jestem na etapie zwiększenia wielkości liczb naturalnych tj. napisanie algorytmu w c++.

Odpowiedz
- Łukasz Kosiński
  says:
  26 lipca, 2017 at 15:01
  
  Daj znać jak Ci się uda. Chętnie to zobaczę 🙂
  
  Odpowiedz
  - Krzysztof
    says:
    19 lipca, 2019 at 09:46
    
    Jako ciekawostkę przedstawiam fraktal Rafała, który można opisać wzorem:
    f(y)= n + x * (-1)^{n} + (3*x + 0.5 – 0.5 * (-1)^{x}) * (n + 0.5 – 0.5 * (-1)^{n})
    gdzie n > 0 i x >0 oraz x,n należy do liczb naturalnych. Liczba x określa kolejne wystąpienie liczby „złożonej” dla n. Dodatkowo zachodzi zależność jezeli:
    x parzyste, n parzyste to f(y) parzyste
    x parzyste, n nieparzyste to f(y) nieparzyste
    x nieparzyste, n parzyste to f(y) nieparzyste
    x nieparzyste, n nieparzyste to f(y) parzyste
    
    Związek liczb złożonych z fraktalem Rafała jest następujący:
    f(z)= 3 * f(y) + 1.5 – 0.5 *(-1)^{x+n}
    gdzie f(y) funkcja generująca liczby tworzące fraktal Rafał dla wartości x i n.
    
    Jeżeli dla wzoru f(y) wprowadzimy ograniczenie x >= n oraz f(y) <= Ym to otrzymamy tzw. sito Małgorzaty w przedziale liczb naturalnych (1,Ym).
    Związek wartości Y z przedziału (1,Ym) z liczbami (złożonymi i pierwszymi) jest następujący:
    f(L)= 3 * Y + 2 dla wartości nieparzystych Y lub
    f(L)= 3 * Y + 1 dla wartości parzystych Y
    oraz f(L) jest liczbą złożoną jeżeli wartość Y została wyznaczona przez f(y).
    
    Odpowiedz

Binarnie.pl

Sito Eratostenesa – algorytm i jego implementacje

Sito Eratostenesa – działanie

Sito Eratostenesa – implementacje

C++

Java

Python

Sito Eratostenesa – co warto wiedzieć?

Podsumowanie

You Might Also Like

Jak wyjść z Vim

Praktyki w Scythe Studio

Praca zdalna jako junior

5 komentarzy

Michał

Hailon

Krzysztof

Łukasz Kosiński

Krzysztof

Dodaj komentarz Anuluj pisanie odpowiedzi