W poprzednich wpisach omówiliśmy sobie czym są liczby pierwsze, a także jak rozkładać liczby na czynniki. Podaliśmy również implementacje jak takie liczby wyznaczać. Będąc w temacie liczb naturalnych, warto dowiedzieć się czym są liczby doskonałe.
Liczby doskonałe to takie liczby, których suma podzielników właściwych (poza nimi samymi) jest równa właśnie tej liczbie. Dzielnikiem właściwym nazywamy dzielnik, który dzieli daną liczbę bez reszty. Dla przykładu podzielnikami liczby 28 są 1, 2, 4, 7, 14, 28. Suma podzielników będzie więc równa: 1 + 2 + 4 + 7 + 14 = 28. Liczby doskonałe występują w zbiorze liczb naturalnych relatywnie rzadko i do tej pory nie znaleziono żadnego schematu w ich występowaniu.
Istnieją również liczby doskonałe drugiego stopnia. Są to liczby, których iloczyn dzielników liczby, poza nią samą, jest równy tej liczbie. Przykładem jest liczba 6: 1 * 2* 3 = 6. Jak sprawdzić, czy liczba jest doskonała? Poniżej omówimy algorytm, a potem przejdziemy do jego implementacji w C++, Javie oraz Pythonie.
Liczby doskonałe — algorytm
Na początek pobieramy liczbę naturalną n od użytkownika. Następnie dobrze jest stworzyć dwie zmienne pomocnicze. Jedna z nich będzie przechowywać sumę dzielników, a druga ich iloczyn. Dzięki temu załatwimy od razu dwie sprawy — sprawdzimy jednocześnie, czy liczba jest doskonała stopnia pierwszego i/lub drugiego. Kolejnym krokiem jest rozpoczęcie iteracji od jedynki do połowy liczby n. W ten sposób znajdziemy wszystkie jej dzielniki. Zwróć uwagę, że iterujemy do połowy liczby n, gdyż dzielenie przez więcej niż jej połowa nigdy nie da całkowitego wyniku. Sprawdzamy każdą iterowaną liczbę, czy jest dzielnikiem właściwym. Wykorzystujemy do tego operator modulo, który zwraca resztę z dzielenia. Powinna ona być równa 0. Jeżeli tak jest, to dodajemy liczbę do pierwszej zmiennej pomocniczej, a drugą zmienną pomocniczą mnożymy. Gdy iteracja się zakończy, sprawdzamy, czy zmienne pomocnicze są równe liczbie n. Następnie, zależnie od wyniku, zwracamy czy i jakiego stopnia liczba jest doskonała.
Powyższy algorytm możemy zaprezentować na schemacie blokowym poniżej. Operator %, jest wyżej wspomnianym działaniem, zwracającym resztę z dzielenia dwóch liczb:
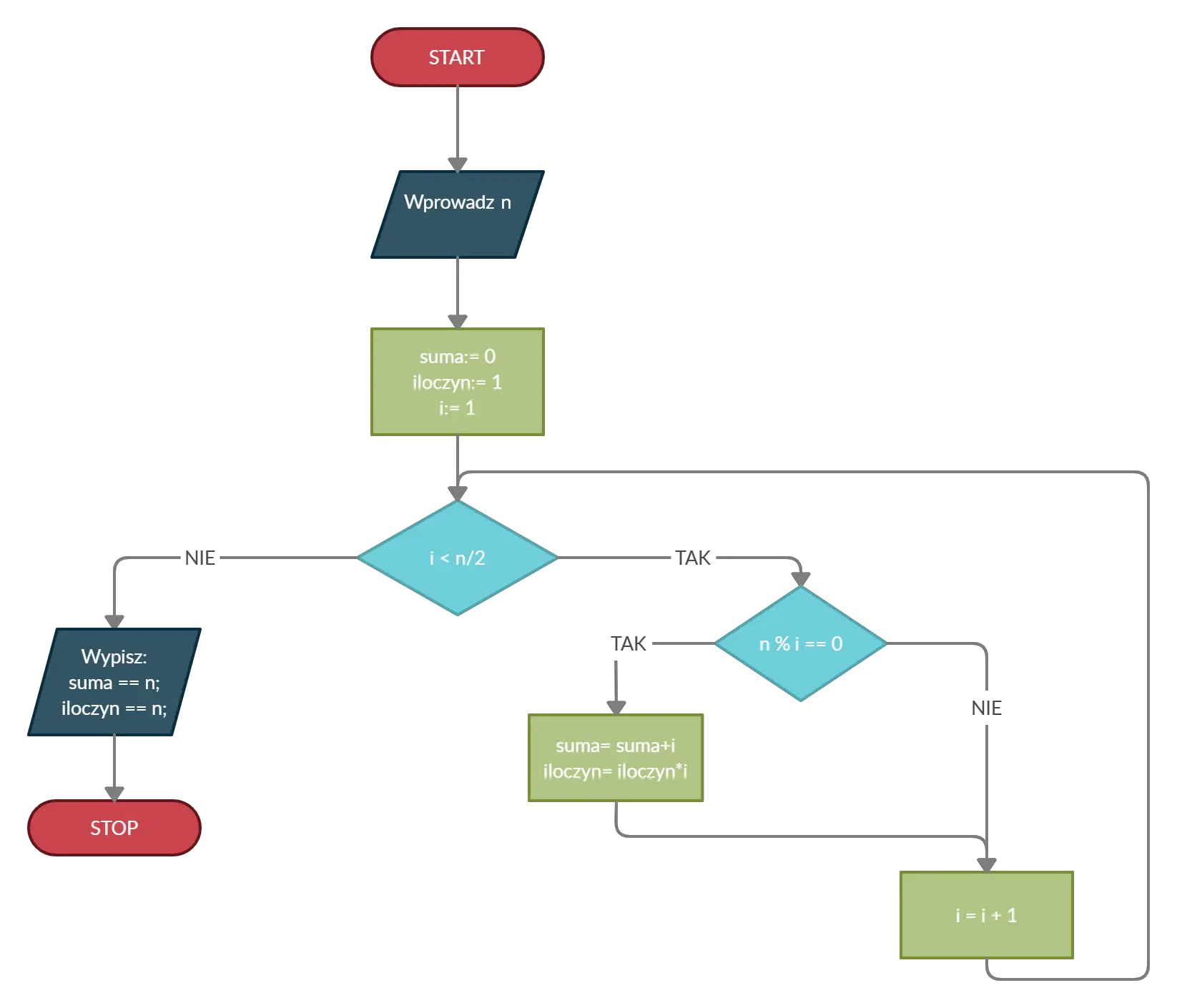
Liczby doskonałe — implementacja C++, Java i Python
Skoro wiemy już jak sprawdzić, czy liczba jest doskonała, przejdźmy zatem do implementacji. Wcielimy w życie powyżej omówiony algorytm, korzystając z trzech popularnych języków programowania. Języki te dostępne są do wyboru na maturze z informatyki, więc możesz sprawdzić działanie programu w tym wybranym przez siebie.
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
//program sprawdzający, czy liczba należy do liczb doskonałych //Kosiński Łukasz #include <iostream> using namespace std; void czy_doskonala(unsigned a) { if(a<1)return;//uwzgledniamy tylko liczby naturalne int suma=0; int iloczyn = 1; for(int i=1; i<=a/2; i++) if(a%i==0) { suma+=i; iloczyn *= i; }//wyznaczamy dzielniki "a", a nastepnie je sumujemy i mnozymy cout << endl << "Liczba " << a << ((suma==a) ? "" : " nie") << " jest liczba doskonala pierwszego stopnia" << endl;//wypisujemy czy liczba jest doskonala pierwszego stopnia cout << "Liczba " << a << ((iloczyn==a)? "" : " nie")<< " jest liczba doskonala drugiego stopnia" << endl;// i drugiego stopnia } int main() { int x; do { cin >> x; czy_doskonala(x); }while(x!=0);//pętla bedzie się wykonywać dopóki nie wpiszemy zera system("pause"); return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
public class Doskonala { public static void main(String[] args) { System.out.println("Program sprawdzający czy liczba a jest liczbą doskonałą."); System.out.println("Podaj liczbę a: "); Scanner scanner = new Scanner(System.in); // inicjalizacja skanera, który będzie pobierał wartości zmiennych int n = scanner.nextInt(); int iloczyn = 1; int suma = 0; for(int i : dzielniki(n)) { iloczyn *= i; suma+= i; } System.out.println(n + " " + ((suma == n) ? "" : "nie ") + "jest liczbą doskonałą."); // zwracamy wynik dla sumy System.out.println(n + " " + ((iloczyn == n) ? "" : "nie ") + "jest liczbą doskonałą drugiego stopnia."); // i dla iloczynu scanner.close(); // zwalniamy zasoby } private static List<Integer> dzielniki(int n){ // tworzymy metodę, która zwraca listę dzielników danej liczby(poza nią samą) ArrayList<Integer> list = new ArrayList<Integer>(); // korzystamy z ArrayList, która pozwala na dynamiczne dodawanie i usuwanie elementów list.add(1); // dzielnikiem każdej liczby jest 1, dodajemy więc od razu do listy for(int i = 2; i <= n/2; i++) { // iterujemy przez wszystkie liczby mniejsze lub równe jej połowie (liczby większe od połowy nie będą już dzieliły jej bez reszty) if(n % i == 0) { // jeżeli iterowana liczba dzieli n bez reszty list.add(i); // to dodajemy do listy } } return list; } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
def dzielniki(x): #definiujemy funkcje, która zwroci wszystkie dzielniki liczby x (poza nia sama) d = [] #tworzymy pomocnicza, na razie pusta tablice for a in range(1, (int(x/2) + 1)): # iterujemy od 1 do polowy liczby wlacznie - dzielenie liczby przez wiecej niz jej polowe nie da wyniku calkowitego if x % a == 0: # jezeli liczba jest podzielna d.append(a) # to dodaj ja do tabeli return d #zwracamy uzupelniona tablice print("Program sprawdzajacy czy liczba n jest doskonala") print("Podaj liczbę n: ") n = int(input()) suma = 0 iloczyn = 1 for i in dzielniki(n): suma += i #zliczamy sume iloczyn *= i #i iloczyn dzielnikow print ("Liczba " + str(n) + ("" if (suma == n) else " nie") + " jest liczba doskonala pierwszego stopnia") print ("Liczba " + str(n) + ("" if (iloczyn == n) else " nie") + " jest liczba doskonala drugiego stopnia") |
Liczby doskonałe — ciekawostki
- Liczby doskonałe występują naprawdę, bardzo, bardzo rzadko. Do dzisiaj znaleziono tylko 43 takie liczby, z czego największa z nich ma aż 18 milionów cyfr.
- Liczba 6 nazywana jest liczbą najdoskonalszą. Jest ona bowiem jedyną, znaną liczbą, która jest jednocześnie doskonała w stopniu pierwszym i drugim.
- Wszystkie znalezione liczby doskonałe są parzyste.
- Nie wiadomo, czy liczb doskonałych jest nieskończenie wiele.
Podsumowanie
W dzisiejszym wpisie skorzystaliśmy z pojęcia dzielników liczby, o którym przeczytasz dokładniej tutaj. Ten i inne algorytmy ułatwią Ci zdanie matury z informatyki. Listę wszystkich moich porad, znajdziesz w tym oto wpisie.







Informatyk
says:Program nie daje odpowiedzi zwrotnej w razie nie zajścia warunku o byciu liczbą całkowitą.