Od początku założeniem bloga było utrwalanie sobie informacji oraz wiedzy na temat szeroko pojętej informatyki i programowania, a w rezultacie uczenie się poprzez nauczanie innych (patrz taksonomia celów nauczania Blooma) do m.in. matury z informatyki. Prawie tydzień się zbierałem żeby rozwiązać sobie zadanka i żeby napisać parę słów od siebie na temat samego egzaminu. Zapraszam do lektury.
Moja opinia
Oceniając cały egzamin pierwszym pytaniem jakie się nasuwa jest: „Trudny czy łatwy?”. To oczywiście moje subiektywne zdanie, ale według mnie matura z informatyki 2017 po zestawieniu z tymi sprzed chociażby roku, czy dwóch lat, była o dobry poziom trudniejsza. Pozostaje oczywiście kwestia trafienia zadań pod siebie. Jednemu bardziej leży napisanie programu, drugiemu np. Excel. Stres i zamieszanie też nie ułatwia życia maturzyście – może dlatego poszło mi gorzej niż się spodziewałem.
A co właściwie skopałem? Teoria przyzwoicie, programy gitarka, Access wybornie, ale ten cholerny Excel 😀 Im dłużej siedziałem nad tym w domu, przygotowując ten wpis, tym bardziej popadałem w rozpacz. Przez swoje gapiostwo nawet nie doczytałem o jaki typ wykresu prosili 😀 Czwarte źle zrozumiałem, a piątego się przestraszyłem i z uwagi na uciekający czas zostawiłem sobie na potem. Potem, które nigdy nie nadeszło… 😉 W typowanie procentowego wyniku bawić się nie będę (szkoda moich nerwów na zamartwianie się tym), ale te zadania z części drugiej, które udało mi się rozwiązać załączam w tym wpisie.
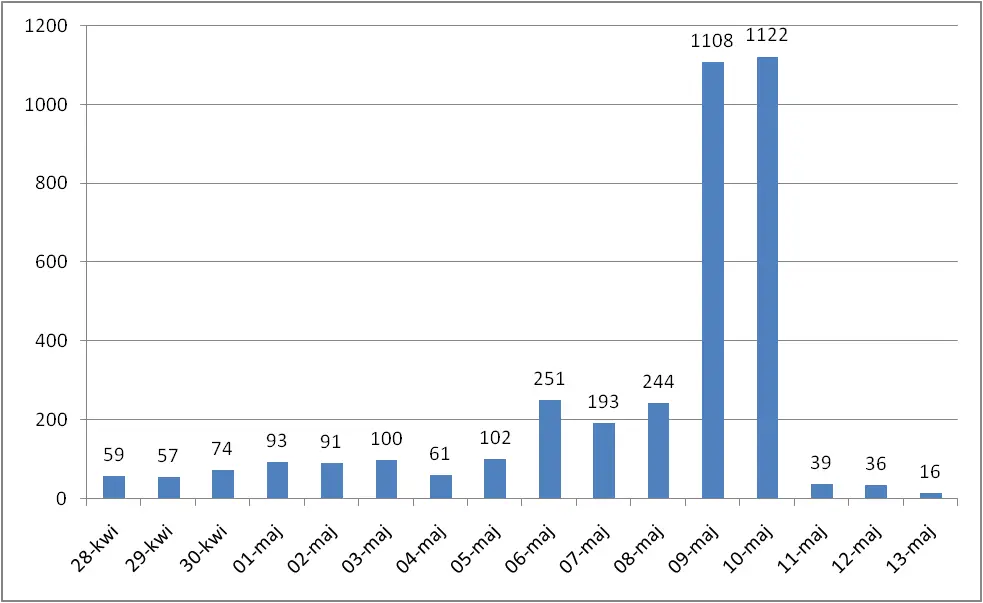
Jeszcze taka mała dygresja. Przed 28 kwietnia wyświetlenia na moim blogu oscylowała w granicach 100 dziennie. Potem było gorzej, w majówkę nadal słabo. Wiadomo, ludzie uczyli się do innych przedmiotów. Za to im bliżej matury tym słupki w moich statystykach rosły, aż tu nagle szok. Dzień przed maturą ponad 1000 odwiedzin 🙂 Potem tak jak przypuszczałem wyswietlenia zmalały (dramatycznie). Zachęcam do zaglądania od czasu do czasu do mnie, gdyż teraz będę się skupiać już na własnych projektach, ciekawostkach, przemyśleniach dotyczących programowania. Słowem mniej o maturze, więcej o developerce. Byłbym też wdzięczny za polecenie mojego bloga młodszym znajomym, którzy również będą podchodzić do matury z informatyki za rok, czy dwa. Zamierzam wszystkie omawiane dotychczas algorytmy wyjaśniać na filmach podobnych do tych Matemaksa. Przed tegoroczną maturą tego nie zrobiłem, ponieważ dość późno wpadłem na pomysł założenia blgoa o takiej tematyce i w efekcie nie zostało wiele czasu na takie ekstrawagancje. Dzięki 😉
Matura z informatyki 2017 rozwiązania cz. 1
Część teoretyczna matury z informatyki z 2017 roku nie należała do najłatwiejszych. Standardowo pojawiła się rekurencja, prosty algorytm w pseudokodzie, a także wybrane zagadnienia z języka SQL. Nie obeszło się jednak bez samodzielnego obliczania wartości funkcji w drugim zadaniu. Zadania, wraz z rozwiązaniami i omówieniem, znajdziecie poniżej.
Matura z informatyki 2017 zadanie 1 – prostokąt
Podpunkt 1
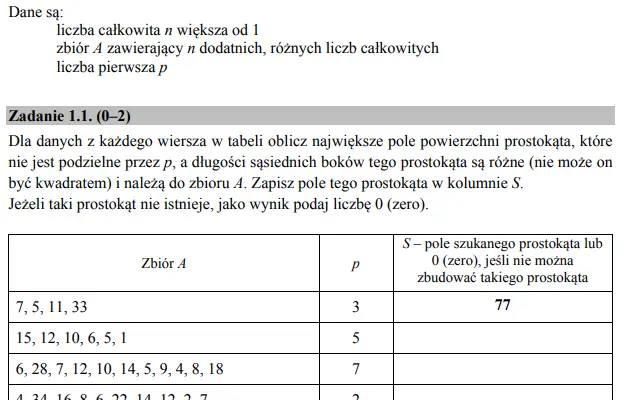
Zadanie jest proste. Musimy obliczyć pole największego prostokąta, który nie jest kwadratem. Jego długości boków muszą zawierać się we zbiorze A. Jednocześnie pole to nie może być podzielne przez liczbę p. Jak zatem to zrobić?
Wystarczy znaleźć dwie największe wartości ze zbioru A, z zastrzeżeniem, że obie nie są podzielne przez liczbę p. W ten sposób ich iloczyn nie będzie przez nią podzielny, a z racji, że wybraliśmy dwie największe liczby, to pole również będzie maksymalne. Najprościej będzie najpierw wyeliminować liczby podzielne przez p, a następnie wybrać dwie największe liczby.
Wykonując powyższe kroki możemy uzupełnić tabelkę:
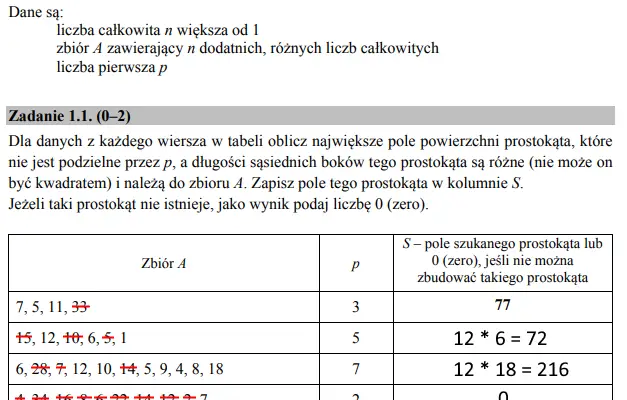
Zwróć uwagę, że w ostatnim wierszu wpisaliśmy zero, gdyż pozostał nam tylko jeden bok, a nie możemy go użyć dwa razy.
Podpunkt 2

W tym podpunkcie musimy utworzyć algorytm, który uniwersalnie wyznaczy pole największego prostokąta dla dowolnego zbioru A i dowolnego dzielnika p. Ze względu na złożoność obliczeniową, która będzie podlegała ocenie, będzie on działać inaczej, niż robiliśmy to w poprzednim punkcie.
W algorytmie tym znajdziemy dwie największe wartości ze zbioru, iterując poprzez wszystkie jego elementy. Sprawdzimy również od razu ich podzielność przez p. Ze względu na to, że to zadanie musimy wykonać bez korzystania z komputera, rozwiązanie proponuję zapisać w postaci listy kroków. Korzystając ze znanego nam języka programowania łatwo możemy popełnić prosty błąd, który bez kompilatora będzie trudno zauważyć.
| max1 = 0 #definiujemy zmienne przechowujace max2 = 0 #dwie maksymalne wartosciS = 0 #zmienna przechowujaca polei = 1 #zmienna iterujacadopóki i <= n: #dopoki nie przejdziemy przez cały zbior A jeżeli A[i] % p != 0: #jezeli aktualny element nie jest podzielny przez p jeżeli A[i] > max1: #jezeli jest wiekszy od pierwszej wartosci max2 = max1 #to ustawiamy go jako pierwszy max max1 = A[i] #a tamten jako drugi w przeciwnym wypadku: jeżeli A[i] > max2: #musimy jeszcze sprawdzic, czy element jest wiekszy niz drugi max max2 = A[i] #i w takim wypadku go podmienic i = i+1 #zwiekszamy zmienna iteracyjna o 1S = max1 * max2 #obliczamy najwieksze pole; jezeli nie znalezlismy dwoch roznych bokow, to bedzie ono rowne 0wypisz S |
Matura z informatyki 2017 zadanie 2 – rekurencja
Podpunkt 1

W podpunkcie tym nie pozostaje nam nic innego, jak rozpisanie kolejnych wywołań funkcji i obliczenie ich wartości. Zauważ, że liczba x będzie dzielona całkowicie przez 2, dopóki nie osiągnie wartości 1. Fakt ten przyda nam się w następnym podpunkcie.
Po prześledzeniu działania algorytmu dla podanych wartości, tabelka powinna wyglądać tak:

Podpunkt 2

Jak już wcześniej zauważyliśmy, funkcja ta będzie dzielić liczbę x przy każdym wywołaniu, dopóki x nie będzie równe 1. Łatwo więc zauważyć, że ilość wywołań jest ściśle powiązana z tym jak blisko liczba x jest kolejnej potęgi dwójki. Jeżeli chcielibyśmy obliczyć największą liczbę x, dla której licz(x) wymaga k wywołań, to musielibyśmy obliczyć 2k . W zadaniu jednak pytają nas o najmniejszą taką liczbę, w związku z czym musimy zmniejszyć k o jeden. Odpowiedzią jest więc B.

Podpunkt 3

W tym podpunkcie ważne jest zrozumienie działania funkcji licz. Zapisz sobie liczby z pierwszego zadania w postaci binarnej. Teraz zera w takim zapisie policz jako -1, a jedynki jako 1 i je zsumuj. Widzisz zależność? Okazuje się, że suma ta jest zgodna z wartością funkcji licz dla tej liczby. Funkcja ta liczy różnicę ilości wystąpień jedynek i zer w zapisie binarnym liczby x. Jeżeli więc chcemy otrzymać sumę równą zero, to oznacza to, że ilość jedynek w zapisie binarnym x musi być równa ilości zer. W związku z tym musimy wziąć liczbę większą od 100. Pierwsza, najbliższa potęga dwójki to 27=128, czyli 100000002. Operując więc na ośmiu bitach, musimy znaleźć taką najmniejszą liczbę, która ma cztery zera i cztery jedynki w zapisie. Najmniejsza liczba będzie taka, która posiada najmniejsze potęgi, wobec czego łatwo zauważyć, że szukaną liczbą jest 10000111=135.

Matura z informatyki 2017 zadanie 3 – prawda/fałsz
Zadanie to, jak co roku, wymagało jedynie znajomości z wiedzy czysto teoretycznej. Pamiętaj jednak, że jakiekolwiek potknięcie oznacza 0 punktów za dany podpunkt.
Podpunkt 1

Podpunkt dosyć prosty. W pierwszym punkcie odpowiedzią jest fałsz, gdyż zapytanie to posortuje według dwóch pól, a nie jednego. Można było się również pomylić przy trzecim wierszu, myśląc że GROUP BY również sortuje wyniki. Pozostałe dwie odpowiedzi spełniają wymagania podpunktu.
Podpunkt 2

Ten podpunkt również nie jest zbyt trudny. W pierwszym wierszu zaznaczyliśmy fałsz, bo pomimo, że tabela może zawierać więcej niż jeden PESEL, to funkcja COUNT powoduje zliczenie tych samych wystąpień. W efekcie każdy PESEL otrzymamy tylko raz. W ostatnim pytaniu trzeba było pamiętać o słowie kluczowym HAVING, przez które w wyniku otrzymamy jedynie te numery PESEL, które wystąpiły więcej niż jeden raz.
Podpunkt 3

Podpunkt ten również nie powinien sprawić nikomu trudności. Jedyną wątpliwą kwestią, jest, według mnie, ostatni wiersz. W dobie szyfrowania i zabezpieczeń ciężko jest już wysłać wiadomość z innym nadawcą.
Matura z informatyki 2017 rozwiązania cz. 2
Pod tym linkiem możecie pobrać arkusz wraz z danymi i moimi rozwiązaniami: LINK.
Zadanie 4.1
To zadanie było dość proste, ja wykonałem je z pomocą Accessa. Szybki import danych z cukier.txt, taka oto kwerenda:
|
1 2 3 4 |
SELECT TOP 3 Cukier.NIP, Sum(Cukier.[Ilość kg]) AS [SumaOfIlość kg] FROM Cukier GROUP BY Cukier.NIP ORDER BY Sum(Cukier.[Ilość kg]) DESC; |
i mamy naszych trzech najlepszych klientów.
| 254-14-00-156 | 27505 |
| 847-48-41-699 | 26955 |
| 392-78-93-552 | 26451 |
Zadanie 4.2
Z tym też sobie poradziłem. Korzystając tym razem z Excela. Wykorzystałem w tym zadaniu formułę JEŻELI. Jeżeli rok danego zamówienia był odpowiedni to ilość kilogramów cukru w zamówieniu mnożyłem przez cenę odpowiednią dla tego roku. Wyszło na to, że przez te wszystkie lata sprzedano cukier za: 643 267,07 zł.
Zadanie 4.3
Jak już wspomniałem to zadanie skiepściłem ze względu na swoje roztargnienie. Niemniej jednak, prawidłowy wykres do tego zadania, powinien wyglądać tak:
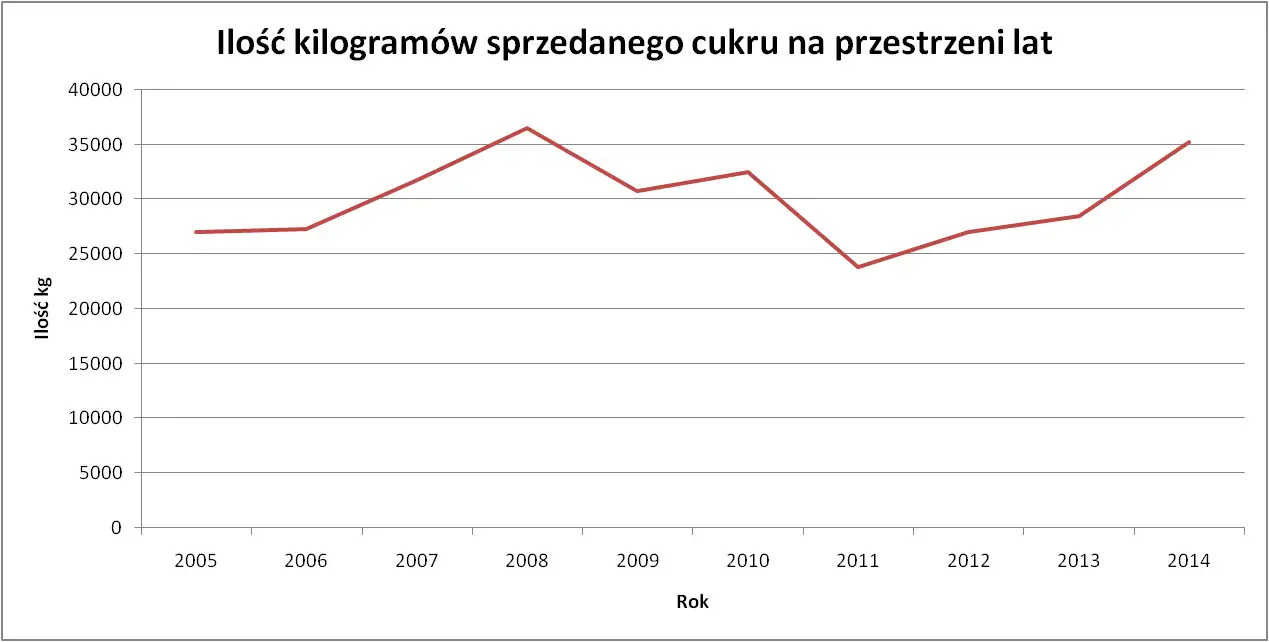
Wykres jest utworzony na podstawie danych, które sumowaliśmy w poprzednim zadaniu.
Zadanie 4.4
Tutaj ponownie Excel. Najpierw musimy upewnić się, że dane są posortowane rosnąco wg daty. Następnie trzeba posortować je według NIP klienta. Potem musimy obliczyć sumę zakupionych dla każdego z nich w oddzielnej kolumnie. Użyłem do tego formuły JEŻELI. Gdy klient wyżej był ten sam, co w danym dniu, to dodawaliśmy do siebie poprzednią i dzisiejszą wartość. W przeciwnym wypadku komórka przyjmowała wartość równą ilości zakupionych dzisiaj kilogramów. Gdy policzyliśmy już ilość zakupionych kg dla każdego klienta, wystarczyło obliczyć rabaty i je wszystkie zsumować. Obliczanie rabatu wykonałem za pomocą trzech, zagnieżdżonych w sobie formuł JEŻELI – pierwsza sprawdzała, czy suma >=10000, druga >=1000, zaś trzecia >=100. Po zsumowaniu wszystkich rabatów powinieneś otrzymać odpowiedź 38126,35 zł.
Zadanie 4.5
Tym razem musimy stworzyć dwie dodatkowe kolumny. Pierwsza będzie zapisywać aktualny stan magazynu dla danego dnia. Trzeba oczywiście posłużyć się formułą JEŻELI, żeby sprawdzić, czy stan magazynu wymagał dokupywania (<5000kg). Jeżeli tak, to korzystamy z funkcji ZAOKR.W.GÓRĘ, która pozwoli nam obliczyć ilość dokupionych kilogramów po 1000kg. Gdy już wypełnimy kolumnę, możemy przystąpić do kolejnej. Tutaj korzystamy z formuły JEŻELI, żeby sprawdzić, czy ilość dokupionego cukru jest >=4000kg. Jeżeli tak, zwracamy wartość jeden. Następnie zsumujemy tą kolumnę i otrzymamy odpowiedź: 14 razy.
Zadanie 5.1
Po topornym Excelu, Access był jak balsam na rany. Podszedł mi. Najpierw inport danych, potem relacje (co z czym wyjaśniać chyba nie ma potrzeby) i jak zwykle kweredny.
|
1 2 3 4 |
SELECT Wyniki.Rodzaj_meczu, Count(Wyniki.Data_meczu) AS PoliczOfData_meczu FROM Druzyny INNER JOIN Wyniki ON Druzyny.Id_druzyny = Wyniki.Id_druzyny GROUP BY Wyniki.Rodzaj_meczu, Druzyny.Miasto HAVING (((Druzyny.Miasto)="Kucykowo")); |
L 113
P 25
T 6
|
1 2 3 4 5 |
SELECT Count(Wyniki.Rodzaj_meczu) AS PoliczOfRodzaj_meczu, Year([Data_meczu]) AS Wyr1 FROM Druzyny INNER JOIN Wyniki ON Druzyny.Id_druzyny = Wyniki.Id_druzyny GROUP BY Year([Data_meczu]), Druzyny.Miasto HAVING (((Druzyny.Miasto)="Kucykowo")) ORDER BY Count(Wyniki.Rodzaj_meczu) DESC; |
Dla świętego spokoju można by było dodać TOP 1 po SELECT, aby uzyskać tylko jeden wynik, ale myślę nie ma potrzeby. Po posortowaniu malejąco według liczby meczów w każdym meczu, wiemy, że w 2007 rozegrano najwięcej – 21 meczów z ekipami z Kucykowa.

Zadanie 5.2
Tutaj stworzyłem dwie kweredny (jedną też da radę). Jedna zlicza łącznie ile bramek w historii Galop Kucykowo strzelił danej drużynie oraz ile bramek stracił. Druga z kwerend operuje na danych z pierwszej i wyświetla tylko te rekordy, dla których suma bramek zdobytych i straconych jest taka sama. Odpowiedzią do tego zadania są zespoły: Nocne Pumy Opole oraz Zwinne Mewy Chojnice.
|
1 2 3 |
SELECT Druzyny.Nazwa, Druzyny.Miasto, Sum(Wyniki.Bramki_zdobyte) AS SumaOfBramki_zdobyte, Sum(Wyniki.Bramki_stracone) AS SumaOfBramki_stracone FROM Druzyny INNER JOIN Wyniki ON Druzyny.Id_druzyny = Wyniki.Id_druzyny GROUP BY Druzyny.Nazwa, Druzyny.Miasto; |
|
1 2 3 |
SELECT [2_1].Nazwa, [2_1].Miasto FROM 2_1 WHERE ((([SumaOfBramki_zdobyte]-[SumaOfBramki_stracone])=0)); |
*tak dla jasności, 2_1 to nazwa pierwszej kweredny
Zadanie 5.3
Tutaj stworzyłem trzy kwerendy. Po jednej dla meczów wygranych, przegranych i zremisowanych. Wystarczyło zauważyć, że jeśli w danym meczu więcej było bramek zdobytych, niż straconych to drużyna ten mecz wygrała. Podobnie działo się w przypadku porażek oraz remisów. Oczywiście rozpatrujemy tylko mecze wyjazdowe, czyli Gdzie=”W”.
|
1 2 3 |
SELECT Count(*) FROM Wyniki WHERE Bramki_zdobyte>Bramki_stracone AND Gdzie="W"; |
To przykład kwerendy wskazującej na to ile mamy meczów wyjazdowych wygranych. Dla przegranych i zremisowanych wystarczy zmienić znak „>” na odpowiednio „<” i „=”.
Odpowiedzią do tego zadania jest:
579 wygranych
452 przegranych
170 zremisowanych
Zadanie 5.4
Nad tym zadaniem siedziałbym chyba dużo dłużej, gdyby nie trochę SQL’a. Trzeba było zauważyć, że jeżeli stworzymy kwerendę wybierającą wszystkie numery licencji sędziów, którzy prowadzili spotkania pucharowe to w gronie tych sędziów nie będzie tych, którzy nie prowadzili żadnego spotkania o puchar.
|
1 2 3 |
SELECT Count(*) AS Ilu_sedziow FROM sedziowie WHERE ((sedziowie.[nr_licencji]) Not In (SELECT nr_licencji FROM wyniki WHERE Rodzaj_meczu="P")); |
Zadanie 6.1
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
#include <iostream> #include <fstream> using namespace std; int main() { fstream plik; plik.open("dane.txt", ios::in); if(!plik) { cout << "No nie"; return 1; }else { int kolor; int najjasniejszy=0, najciemniejszy=255; while(plik >> kolor) { if(kolor>najjasniejszy) najjasniejszy=kolor; if(kolor < najciemniejszy) najciemniejszy=kolor; } cout << najjasniejszy << " " << najciemniejszy; plik.close(); } return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
package matura; import java.io.BufferedReader; import java.io.File; import java.io.FileReader; import java.io.IOException; public class Main { public static void main(String[] args) throws IOException { File f = new File("dane.txt"); if(!f.exists()) { System.out.println("Podany plik nie istnieje."); return; } BufferedReader br = new BufferedReader(new FileReader(f)); int max = 0; int min = 255; if(br.ready()) { String line; while((line = br.readLine()) != null) { String[] points = line.split(" "); for(String point : points) { int i = Integer.parseInt(point); if(i > max) max = i; else if(i < min) min = i; } } } System.out.println("Najjaśniejszy: " + max); System.out.println("Najciemniejszy: " + min); br.close(); } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
file = open("dane.txt", "r").read().split('\n') max = 0 min = 255 for line in file: if len(line.split(" ")) < 2 or len(line.split(" ")[1]) < 1: continue points = line.split(" ") for point in points: if int(point) > max: max = int(point) else: if int(point) < min: min = int(point) print("Min: " + str(min)) print("Max: " + str(max)) |
Zadanie 6.2
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
#include <iostream> #include <fstream> using namespace std; int main() { fstream plik; plik.open("dane.txt", ios::in); if(!plik) { cout << "No nie"; return 1; }else { int kolor[320]; int licznik=0; int i=0; while(plik >> kolor[i]) { if(i==319) { for(int j=0; j < 320; j++) { if(kolor[j]!=kolor[319-j]) { licznik++; break; } } i=0; } else i++; } cout << licznik; plik.close(); } return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
package matura; import java.io.BufferedReader; import java.io.File; import java.io.FileReader; import java.io.IOException; public class Main { public static void main(String[] args) throws IOException { File f = new File("dane.txt"); if(!f.exists()) { System.out.println("Podany plik nie istnieje."); return; } BufferedReader br = new BufferedReader(new FileReader(f)); int[][] img = new int[200][320]; if(br.ready()) { String line; int iterator = 0; while((line = br.readLine()) != null) { String[] points = line.split(" "); if(points.length < 2) continue; for (int i = 0; i < 320; i++) { img[iterator][i] = Integer.parseInt(points[i]); } iterator++; } int count = 0; for (int i =0; i < 200; i++) { for(int j = 0; j < 320; j++) { if(img[i][j] != img[i][319-j]) { count++; break; } } } System.out.println("Min: " + count); } br.close(); } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 |
file = open("dane.txt", "r").read().split('\n') min = 0 for line in file: if len(line.split(" ")) < 2 or len(line.split(" ")[1]) < 1: continue points = line.split(" ") for i in range(320): if points[i] != points[319-i]: min += 1 break print("Min do usunięcia: " + str(min)) |
Zadanie 6.3
Moja propozycja rozwiązania tego zadania wydaje mi się sensowna. Wyszło mi 753 kontrastujące piksele.
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
#include <iostream> #include <fstream> #include <math.h> using namespace std; bool getNearContrast(int x, int y, int all[200][320]){ if(x != 0){ if(abs(all[x][y] - all[x-1][y]) > 128) return true; } if(x != 199){ if(abs(all[x][y] - all[x + 1][y]) > 128) return true; } if(y != 319){ if(abs(all[x][y] - all[x][y+1]) > 128) return true; } if(y != 0){ if(abs(all[x][y] - all[x][y-1]) > 128) return true; } return false; } int main() { fstream plik; plik.open("dane.txt", ios::in); if(!plik) { cout << "No nie"; return 1; }else { int obraz[200][320]; int i=0; int i2=0; while(plik >> obraz[i][i2]) { i2++; if(i2 == 320){ i++; i2=0; } } int kontrast = 0; for(int i = 0; i < 200; i++){ for(int j = 0; j < 320; j++){ if(getNearContrast(i, j, obraz)) kontrast++; } } cout << kontrast << endl; plik.close(); } return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 |
package matura; import java.io.BufferedReader; import java.io.File; import java.io.FileReader; import java.io.IOException; import java.util.ArrayList; public class Main { public static int getNearContrast(int x, int y, int[][] img){ ArrayList<Integer[]> near = new ArrayList<Integer[]>(); if(x>=0 && x<200 && y>=0 && y < 320) { if(x != 0) near.add(new Integer[] {x-1, y}); if(x != 199) near.add(new Integer[] {x+1, y}); if(y != 0) near.add(new Integer[] {x, y-1}); if(y != 319) near.add(new Integer[] {x, y+1}); } int c = 0; for(Integer[] points : near) { if(Math.abs(img[x][y] - img[points[0]][points[1]]) > 128) { c++; } } return c; } public static void main(String[] args) throws IOException { File f = new File("dane.txt"); if(!f.exists()) { System.out.println("Podany plik nie istnieje."); return; } BufferedReader br = new BufferedReader(new FileReader(f)); int[][] img = new int[200][320]; if(br.ready()) { String line; int iterator = 0; while((line = br.readLine()) != null) { String[] points = line.split(" "); if(points.length < 2) continue; for (int i = 0; i < 320; i++) { img[iterator][i] = Integer.parseInt(points[i]); } iterator++; } int count = 0; for (int i =0; i < 200; i++) { for(int j = 0; j < 320; j++) { if(getNearContrast(i, j, img) > 0) { count++; } } } System.out.println("Kontrastujace: " + count); } br.close(); } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
import math def nearContrasting(x, y, all): if x != 0: if math.fabs(all[x][y] - all[x-1][y]) > 128: return True if x != 199: if math.fabs(all[x][y] - all[x + 1][y]) > 128: return True if y != 319: if math.fabs(all[x][y] - all[x][y+1]) > 128: return True if y != 0: if math.fabs(all[x][y] - all[x][y-1]) > 128: return True return False file = open("dane.txt", "r").read().split('\n') all = [[0 for x in range(320)] for y in range(200)] counter = 0 contrasting = 0 for line in file: if len(line.split(" ")) < 2 or len(line.split(" ")[1]) < 1: continue points = line.split(" ") for i in range(320): all[counter][i] = int(points[i]) counter +=1 for i in range(200): for j in range(320): if nearContrasting(i, j, all): contrasting += 1 print("Punktów kontrastujących: " + str(contrasting)) |
Zadanie 6.4
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
#include <iostream> #include <fstream> #include <algorithm> using namespace std; int main() { fstream plik; plik.open("dane.txt", ios::in); if(!plik) { cout << "No nie"; return 1; } else { int kolor[64000]; int najdluzszy[320]; int tymczasowa[320]; int i = 0; for (int j = 0; j < 320; j++) najdluzszy[j] = 1; for (int j = 0; j < 320; j++) tymczasowa[j] = 1; while (plik >> kolor[i]) { if (i >= 320) { if (kolor[i] == kolor[i - 320]) tymczasowa[i % 320]++; if (kolor[i] != kolor[i - 320]) tymczasowa[i % 320] = 1; if (tymczasowa[i % 320] > najdluzszy[i % 320]) najdluzszy[i % 320] = tymczasowa[i % 320]; } i++; } sort(najdluzszy, najdluzszy + 320); cout << najdluzszy[319]; plik.close(); } return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 |
package matura; import java.io.BufferedReader; import java.io.File; import java.io.FileReader; import java.io.IOException; public class Main { public static void main(String[] args) throws IOException { File f = new File("dane.txt"); if(!f.exists()) { System.out.println("Podany plik nie istnieje."); return; } BufferedReader br = new BufferedReader(new FileReader(f)); int[][] img = new int[320][200]; if(br.ready()) { String line; int iterator = 0; while((line = br.readLine()) != null) { String[] points = line.split(" "); if(points.length < 2) continue; for (int i = 0; i < 320; i++) { img[i][iterator] = Integer.parseInt(points[i]); } iterator++; } int count = 0; for (int i =0; i < 320; i++) { int cmax = 0; int c = 0; for(int j = 1; j < 200; j++) { if(img[i][j] == img[i][j-1]) { c++; } else { if(c>cmax) { cmax = ++c; } c = 0; } } if(count < cmax) { count = cmax; } } System.out.println("Najdluzsza kolumna: " + count); } br.close(); } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
file = open("dane.txt", "r").read().split('\n') all = [[0 for x in range(200)] for y in range(320)] counter = 0 inline = 0 for line in file: if len(line.split(" ")) < 2 or len(line.split(" ")[1]) < 1: continue points = line.split(" ") for i in range(320): all[i][counter] = int(points[i]) counter +=1 for i in range(320): cmax = 0 c = 0 for j in range(200): if all[i][j] == all[i][j-1]: c += 1 else: if c > cmax: cmax = c+1 c = 0 if inline < cmax: inline = cmax print("Najdluzsza kolumna pixeli tego samego koloru: " + str(inline)) |
Jeżeli dotarłeś, aż tutaj to dziękuję i trzymam kciuki za satysfakcjonujący wynik :).






Redc4ke
says:W Excelu ma wyjść 13 razy 4000kg, nie 14
Tomson_Johnson
says:void zad_c()
{
odczyt.open(„dane.txt”);
zapis.open(„wyniki.txt”, ios::app);
int tab[200][320];
int licznik=0, zmienna;
int x=0,z=0;
while(odczyt>>zmienna)
{
tab[x][z]=zmienna;
z++;
if(z==320)
{
z=0;
x++;
}
}
for(int j=0;j<200;j++)
{
for(int i=0;i=0) && (abs(tab[j][i-1]-tab[j][i])>128))
{
licznik++;
continue;
}
//prawo
if((i+1128))
{
licznik++;
continue;
}
//gora
if((j-1>=0) && (abs(tab[j-1][i]-tab[j][i])>128))
{
licznik++;
continue;
}
//dol
if((j+1128))
{
licznik++;
continue;
}
}
}
zapis<<"zad_c: "<<licznik;
zapis.close();
odczyt.close();
}
^Kod działający poprawnie do zadania 6.3
Bartek
says:Co prawda to dość stary post, ale może ktoś pomoże. Mam mały probem z zadaniem 6.2. Mój program daje wyniki o 1 większe od poprawnego. Byłby ktoś tak miły i mi wytłumaczył dlaczego?
Kod:
#include
#include
int main()
{
std::ifstream input;
input.open(„przyklad.txt”);
if (input.fail())
{
std::cout << "Err \n";
input.close();
return 0;
}
int pix[320];
int min = 0;
while (!input.eof())
{
for (int i = 0; i > pix[i];
}
for(int i = 0; i < 320; i++)
{
if(pix[i] != pix[319 – i])
{
min++;
break;
}
}
}
std::cout << "Minimum: " << min << "\n";
input.close();
return 0;
}
Weronika :)
says:DZIĘKI ! 😀
Marta
says:dziękuje, mam te zadania do zrobienia do domu i w życiu bym nawet ich nie ruszyła, dziekuje, wydłużyłeś mój brak jedynki o jedną lekcje 😀 zazdroszcze takiego programistycznego mózgu 😀
Łukasz Kosiński
says:Kłaniam się nisko!