W poprzednim wpisie omawialiśmy czym są dzielniki liczb i jak je w sposób programistyczny znaleźć. Kolejnym, ważnym algorytmem jest algorytm znajdowania największego wspólnego dzielnika dwóch liczb. Wielu z Was pewnie teraz puka się po głowie, myśląc „po co to, na co to komu?”, jednak z algorytmem tym można się spotkać nawet w sytuacji codziennej. Wyobraź sobie, że masz ułamek 850/6625, a twoim zadaniem jest przedstawić go w postaci nieskracalnej. Co robisz jako pierwsze? Szukasz liczby, która podzieli jednocześnie licznik i mianownik bez pozostawiania reszty. Jako pierwsza na myśl nasuwa się liczba pięć — po skróceniu mamy 170/1325 — znowu możemy skrócić przez 5. Ułamek ten w postaci nieskracalnej wynosi więc 34/265. Podzieliliśmy obie liczby dwukrotnie przez 5, co oznacza, że ich największym wspólnym dzielnikiem była liczba 25. W ten sposób, choć może nieświadomie, wyznaczasz największy wspólny dzielnik dla dwóch liczb. W dzisiejszym wpisie omówimy zatem jak wyznaczyć NWD dwóch liczb naturalnych i przedstawimy sobie implementacje w trzech popularnych językach programowania.
Algorytm wyznaczania największego wspólnego dzielnika
Zanim zaczniemy tworzyć implementacje, skonstruujemy najpierw algorytm, który opierać będziemy na istniejącym już algorytmie Euklidesa — wybitnego, greckiego matematyka. Skoro wyznaczamy NWD dwóch liczb, to musimy najpierw je pobrać od użytkownika — oznaczymy je jako n i k. Z racji, iż nie narzucamy użytkownikowi, że ma najpierw podać liczbę mniejszą, a potem większą, musimy w algorytmie rozróżnić która jest większa, a która mniejsza. Jeżeli więc n>k, to przy użyciu operatora modulo wyznaczymy resztę z dzielenia z n/k. W przeciwnym wypadku wyznaczymy resztę dzielenia z k/n. Jeżeli reszta ta będzie równa 0 (co oznacza, że liczba mniejsza jest dzielnikiem pierwszej), to drukujemy mniejszą liczbę jako wynik. W przeciwnym wypadku wywołujemy algorytm od nowa, z tym że wprowadzona zostanie mniejsza z tych dwóch liczb oraz wspomniana reszta z dzielenia.
Zjawisko, w którym algorytm wywołuje sam siebie, nazywamy rekurencją, o której przeczytasz dokładniej tutaj. Algorytm będzie wykonywał się, dopóki nie natrafi sytuacji, w której liczby będą przez siebie podzielne — będzie oznaczało to koniec jego pracy i odnalezienie wyniku. Algorytm ten możemy przedstawić na schemacie blokowym:
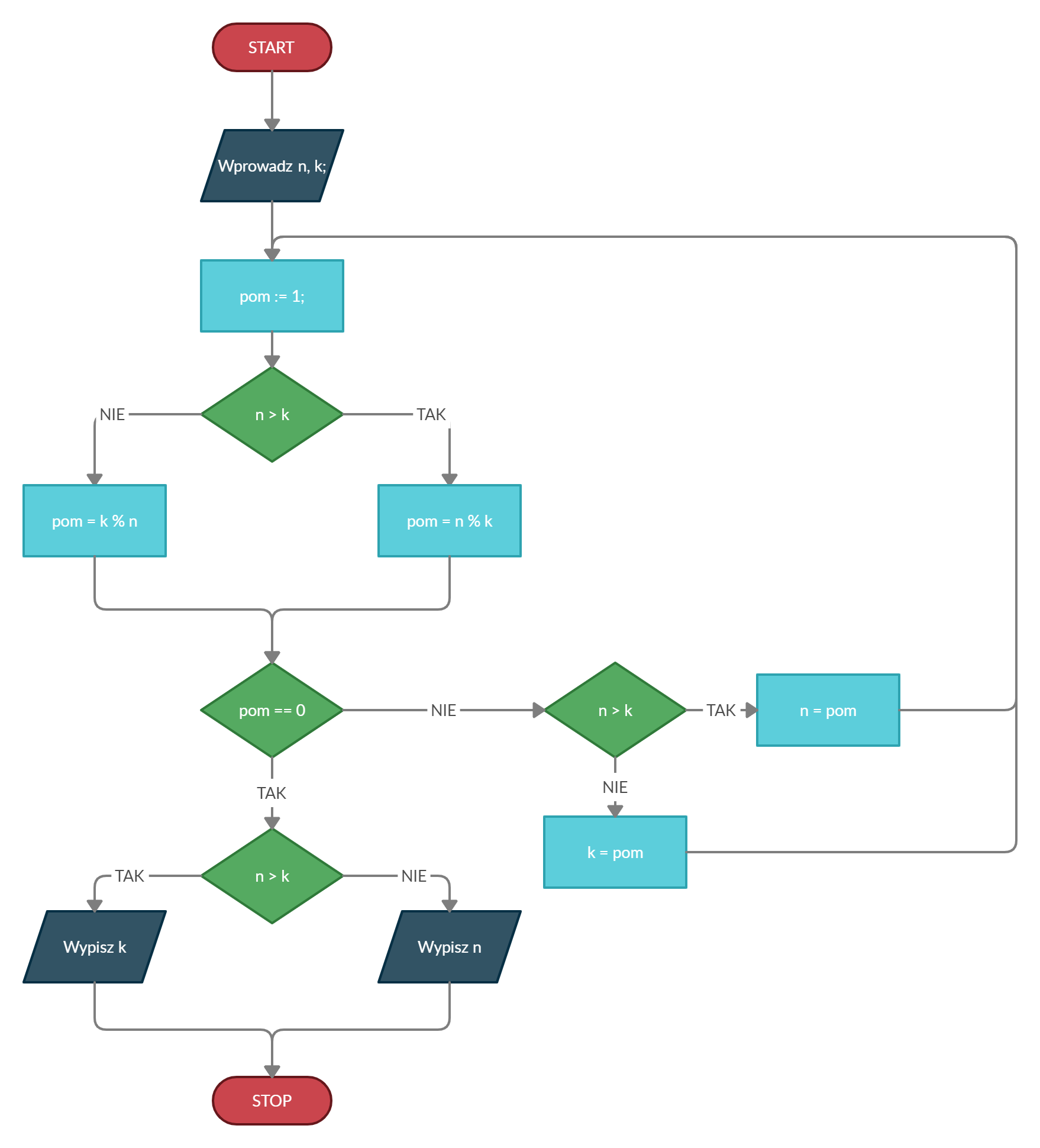
Wyznaczanie największego wspólnego dzielnika w C++, Java i Python
Mając już rozpisany algorytm, możemy przystąpić do jego implementacji. Algorytm wyznaczania NWD pojawia się w wymaganiach na maturę z informatyki, dlatego postanowiłem pokazać jak zaimplementować go w trzech językach, które mamy do wyboru decydując się na to rozszerzenie.
Największy wspólny dzielnik – implementacja C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
//program rekurencyjny wyliczający NWD dla dwóch liczb //Kosiński Łukasz #include <iostream> using namespace std; unsigned nwd(unsigned a, unsigned b) { unsigned pom= (a>b)?a%b:b%a;// program przypisuje zmiennej pomocniczej resztę z dzielenia większej liczby przez mniejszą if(pom==0)return (a>b)?b:a;//jeśli modulo z dwóch liczb wynosi zero to wynikiem jest mniejsza z nich return (a>b)? nwd(pom,b) : nwd(pom,a);//jeśli modulo jest różne od 0 to program rekurencyjnie wylicza nwd dla zmiennej pom. i mniejszej z liczb } int main() { unsigned x,y; cin >> x >> y;//wprowadzamy dwie liczby całkowite cout << nwd(x,y) << endl; return 0; } |
Największy wspólny dzielnik – implementacja Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
import java.util.Scanner; public class NWD { private static int nwd(int a, int b) { int c = (a>b) ? a%b : b%a; // korzystamy tutaj ze zmiennej pomocniczej i prostego wyrażenia warunkowego if(c==0) return (a>b) ? b : a; // warunek STOP funkcji rekurencyjnej; gdy reszta z dzielenia dwóch liczb jest równa zero, to zwróć tą mniejszą (jest ona poszukiwanym dzielnikiem) return (a>b) ? nwd(c, b) : nwd(c, a); // w innym wypadku wywołujemy metodę jeszcze raz } public static void main(String[] args) { Scanner scanner = new Scanner(System.in); // inicjalizujemy Scanner - obiekt, który będzie zczytywał dane od użytkownika System.out.println("Program obliczający największy wspólny dzielnik."); System.out.println("Podaj pierwszą liczbę: "); int a = scanner.nextInt(); // pobieramy zmienną od użytkownika System.out.println("Podaj drugą liczbę: "); int b = scanner.nextInt(); // pobieramy zmienną od użytkownika scanner.close(); // zwalniamy zasoby System.out.println("Największy wspólny dzielnik liczb " + a + " i " + b + " to: " + nwd(a, b)); // wywołujemy metodę przy drukowaniu wyniku } } |
Największy wspólny dzielnik – implementacja Python
|
1 2 3 4 5 6 7 8 9 10 11 12 |
def nwd(x, y): #definiujemy funkcje do późniejszego użycia z = x % y if (x > y) else y % x # obliczamy reszte dzielenia z liczb (wykorzystujemy tu wyrażenie warunkowe) if z == 0: return y if (x > y) else x #jeżeli reszta ta jest rowna 0, to wynikiem jest mniejsza z liczb return nwd(z, y) if x > y else nwd(z, x) # w przeciwnym wypadku rekurencyjnie sprawdzamy NWD reszty dzielenia z mniejsza liczba print("Program znajdujacy najwiekszy wspolny dzielnik dwoch liczb") print("Podaj liczbę a: ") a = int(input()) print("Podaj liczbę b: ") b = int(input()) print(nwd(a, b)) |
Największy wspólny dzielnik — ciekawostki
- Aby obliczyć NWD dla trzech liczb, wystarczy wyznaczyć p = NWD dwóch pierwszych liczb, a następnie policzyć NWD dla wcześniej p i ostatniej liczby.
- Największy wspólny dzielnik możemy inaczej zapisać jako iloczyn liczb pierwszych, będących wspólnymi czynnikami dla obu liczb.
- Pierwsze wzmianki o tym algorytmie znajdziemy w dziele „Elementy” Euklidesa — stąd też jego nazwa
- NWD możemy użyć, aby obliczyć najmniejszą wspólną wielokrotność, o czym dowiesz się tutaj.
Algorytm wyznaczania największej wspólnej wielokrotności to tylko jeden z wielu wymaganych przez CKE. Listę pozostałych algorytmów, wraz z odnośnikami do ich omówienia znajdziesz w tym wpisie.





