Matematyka i informatyka to dwie, przeplatające się dziedziny nauki, w których główną rolę odgrywają, rzecz jasna, liczby. Śmiało można również stwierdzić, że bez matematyki nie istniałaby informatyka. Nic więc dziwnego, że prawie wszystkie algorytmy i działania występujące w matematyce, znajdują swoje miejsce również w świecie programistycznym.
Jednym z takich działań jest silnia. Silnią liczby n nazwiemy iloczyn wszystkich dodatnich liczb naturalnych mniejszych bądź równych n, z zastrzeżeniem, że silnia z zera jest równa jeden. Silnię z liczby n zapisujemy jako n!, a czytamy jako n silnia. Przykładowo 4! czytamy jako cztery silnia, a liczymy, mnożąc ze sobą 1*2*3*4 = 4! = 24. Jeżeli się przyjrzysz dokładniej, to zauważysz, że dla dowolnej liczby naturalnej n > 0, n! = (n—1)! * n. Przyda nam się ten fakt przy omawianiu algorytmu, a także podczas implementacji silni w C++, Javie i Pythonie, które znajdziesz poniżej.
Algorytm obliczania silni — dwa sposoby
Silnie z n możemy przedstawić jako iloczyn liczb całkowitych dodatnich mniejszych bądź równych n, ale też ze wzoru (n—1)!*n — mamy zatem dwa sposoby:
Iteracja
Obliczymy silnię, tworząc pętlę, w której zaczynamy od liczby 1, kończąc na liczbie równej n. Tworzymy również zmienną pomocniczą, która początkowo przyjmuje wartość jeden, a następnie, w trakcie iteracji, będziemy mnożyć ją przez aktualnie iterowaną liczbę. W ten sposób przemnożymy przez siebie wszystkie liczby naturalne dodatnie mniejsze lub równe n, a następnie zwrócimy zmienną pomocniczą, która przechowywała wynik. Algorytm ten przewiduje sytuację, w której użytkownik wprowadził zero — zwróci on od razu zmienną pomocniczą (jeden), gdyż iteracja nawet się nie rozpocznie, ponieważ warunek iteracyjny nie zostanie spełniony (1, od której zaczynamy iterację, jest mniejsza od 0). Algorytm iteracyjny silni przedstawiłem na poniższym schemacie blokowym:
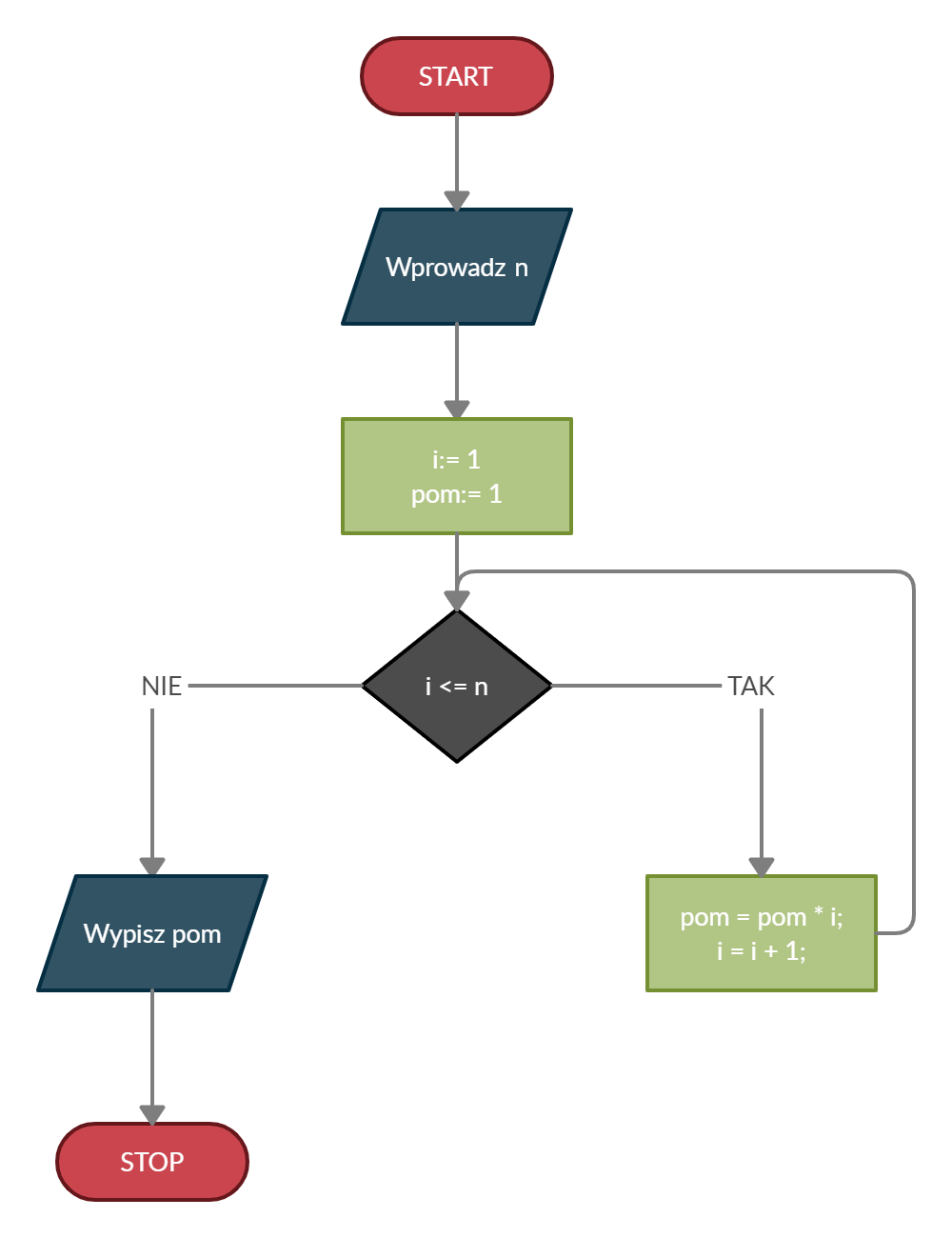
Rekurencja
Skoro wiemy, że n! = (n—1)! * n, to możemy wykorzystać tutaj rekurencję, czyli zabieg, w którym funkcja wywołuje samą siebie. Jeżeli chcesz zgłębić temat rekurencji, to odsyłam cię do tego wpisu. Dla dowolnego n > 0 algorytm będzie wykonywał się, aż nie dojdzie do 0! równego 1, następnie będzie to mnożył przez kolejne, wywoływane wartości n. Cały algorytm przedstawiłem na poniższym schemacie blokowym:
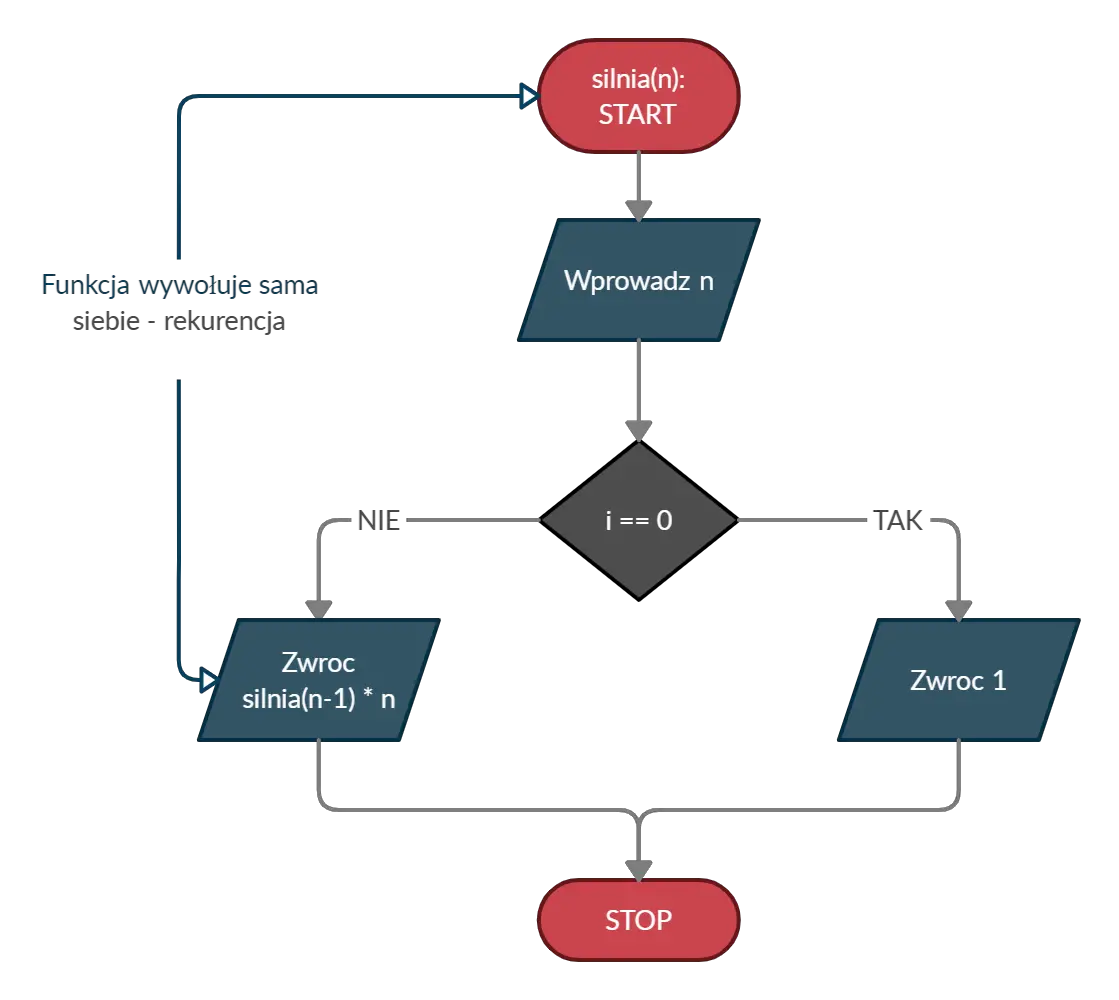
Który algorytm wybrać?
Z reguły rekurencja jest znacznie krótsza w zapisie i czytelniejsza dla programisty, niż iteracja. Jej wadą jest jednak zazwyczaj większa zasobożerność. W tym jednak wypadku, w którym liczymy silnie, ilość wywołań dla obu algorytmów jest taka sama. Możemy więc śmiało korzystać z prostszej, przejrzystszej wersji — rekurencji. Pamiętaj jednak, że wiele innych algorytmów lepiej jest jednak wykonać metodą iteracyjną. Przykładem jest algorytm obliczania wyrazu z ciągu Fibonacciego, który przy implementacji rekurencyjnej jest bezlitosnym pożeraczem zasobów.
Silnia liczby — implementacja w C++, Pythonie i Javie
Jako, że silnia to jeden z najbardziej podstawowych algorytmów, a Ty zapewne robisz sobie z nich powtórkę, zaimplementowałem rekurencyjną metodę obliczania silni w trzech, znanych językach: C++, Javie oraz Pythonie.
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
//program obliczający silnie danej liczby //Kosiński Łukasz #include <iostream> using namespace std; unsigned long long silnia(int a) { if(a==0) return 1; else return a*silnia(a-1); } int main() { int x; do { cin >> x; cout << silnia(x) << endl; }while(x!=55);//pętla bedzie się wykonywać dopóki nie wpiszemy liczby 55 return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import java.util.Scanner; public class Silnia { public static void main(String[] args) { System.out.println("Program liczacy silnie"); System.out.println("Podaj liczbę: "); Scanner scanner = new Scanner(System.in); // inicjalizacja skanera, który będzie pobierał wartości zmiennych int n = scanner.nextInt(); // pobieramy liczbe od uzytkownika System.out.println("Silnia z liczby: "+ n + " wynosi " + silnia(n)); //drukujemy liczbę scanner.close(); //zwalniamy zasoby } private static int silnia(int n) { //tworzymy rekurencyjną metodę liczącą silnię if(n==0) //warunek stop - silnia z 0 jest równa 1 return 1; return silnia(n-1) * n; } } |
Python
|
1 2 3 4 5 6 7 8 |
def silnia(x): #definiujemy rekurencyjna funkcje do późniejszego użycia if x==0: #warunek stop rekurencji - silnia z zera to jeden return 1 return silnia(x-1) * x #wykorzystujemy fakt, ze dla dowolnej n>0, n! = (n-1)! * n print("Program liczacy silnie") print("Podaj liczbę a: ") a = int(input()) print(silnia(a)) |

Jeżeli planujesz zrobić dobrą powtórkę przed maturą z informatyki albo, po prostu, jesteś głodny wiedzy, koniecznie sprawdź ten post. Znajdziesz tam pozostałe, wymagane na egzamin algorytmy, a także inne rzeczy, na które warto zwrócić uwagę przy nauce.





