Matura z informatyki i system binarny to nierozerwalny duet. W tym wpisie swoją uwagę poświęcę właśnie pojęciu systemu binarnego i jego konwersji na lepiej nam znany system dziesiętny.
Jest 10 rodzajów ludzi. Ci, którzy rozumieją system binarny i ci, którzy go nie rozumieją.
System binarny jest najprostszym znanym systemem pozycyjnym, czyli takim, w którym pozycja liczby ma znaczenie. Do zapisu liczby w systemie binarnym używa się dwóch cyfr: zera i jedynki (stąd nazwa dwójkowy).

Już niebawem rusza kurs przygotowujący do matury z informatyki.
Nie daj się zaskoczyć na maturze – zapisz się do listy mailingowej już teraz!
System dwójkowy przyjął się szczególnie w elektronice, gdzie początkowo używany był do opisu dwóch stanów prądu: 0 — brak prądu, 1 — obecność prądu. Jako że bez prądu żadne urządzenie cyfrowe nie ma racji bytu, to system ten znalazł swoje zastosowanie w szeroko pojętej informatyce. Przykładem liczby binarnej jest 10000 (16 w systemie dziesiętnym), 1001001 (73).
Jak wejść głębiej w świat IT i C++’a?
Jeśli chcesz zgłębić wiedzę o nowoczesnych technologiach IT, zapraszamy do śledzenia Somco Software. Firma ta, specjalizująca się w C++ i Qt, regularnie publikuje treści na swoim blogu oraz profilach firmowych. Możesz tam znaleźć cenne informacje, które pomogą Ci lepiej zrozumieć branżę IT i wspomniane technologie.
Jak zamieniać liczby binarne na dziesiętne?
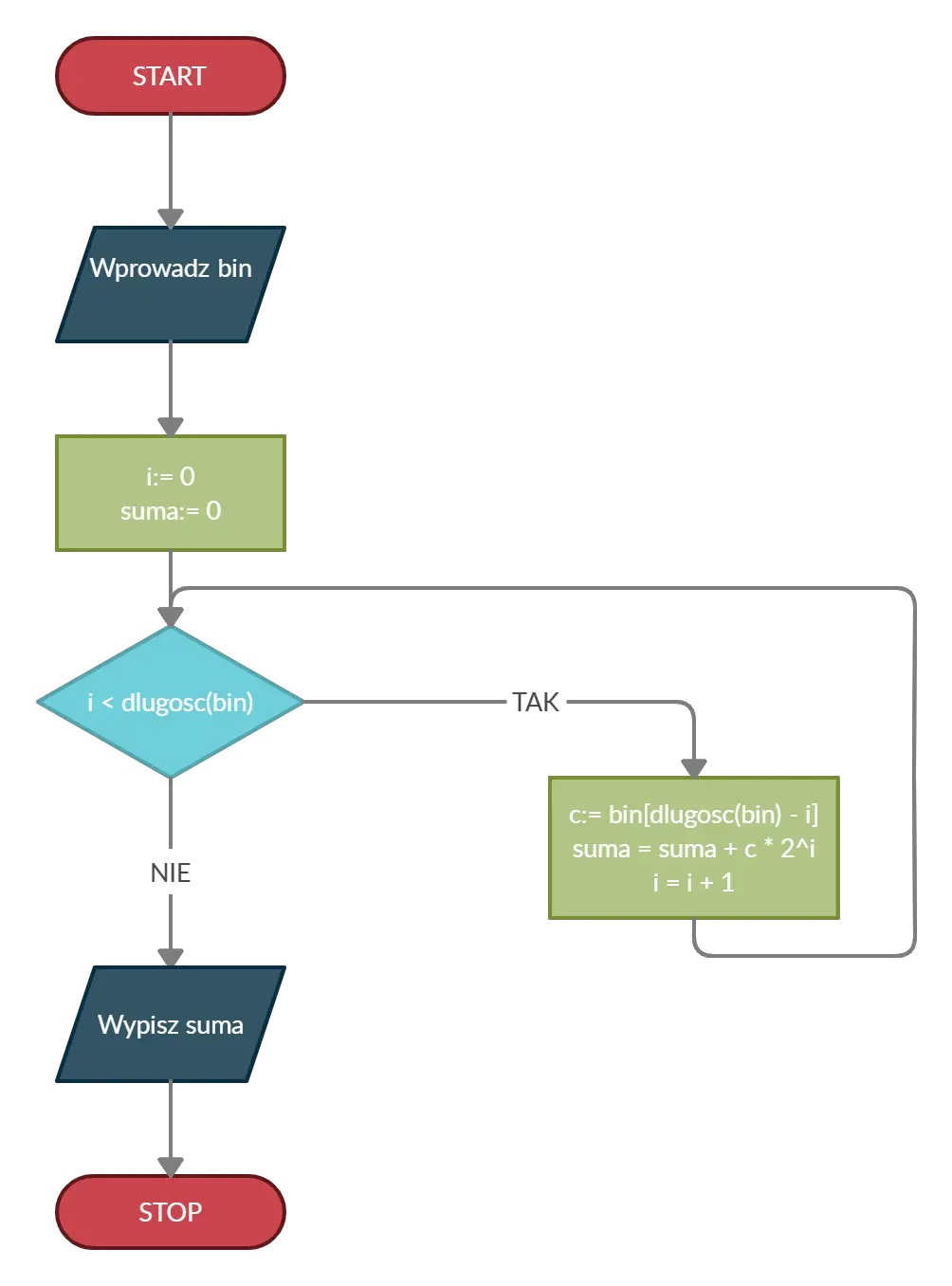
System dwójkowy zawdzięcza swoją nazwę nie bez powodu. Konwersja polega na dodawaniu iloczynów kolejnych potęg dwójki i odpowiadającym im cyfr z liczby binarnej. Przy zamianie liczby z systemu binarnego na dziesiętny musimy zacząć od końca liczby. Spójrzmy, dla przykładu, na liczbę 10100:
- Bierzemy pierwszą cyfrę od końca: 0. Potęgi dwójki zaczynamy od wykładnika 0. W takim razie 0 * 20 = 0 * 1 = 0;
- Bierzemy kolejną cyfrę od końca: 0. Kolejny wykładnik dwójki to 1, więc 0 * 21 = 0 * 2 = 0;
- Trzecia od końca jest 1. Wykładnik dwójki zaczęliśmy od zera, wykonujemy więc działanie 1 * 22 = 1 * 4 = 4;
- Kolejna cyfra od końca to 0: 0 * 23 = 0 * 8 = 0;
- Ostatnia od końca cyfra to 1. Działanie ma postać 1 * 24 = 1 * 16 = 16;
- Na koniec sumujemy wszystkie wyniki działań: 0 + 0 + 4 + 0 + 16 = 20. Liczba 10100 w systemie dziesiętnym ma więc wartość 20.
Ten sposób konwersji można wykorzystać właściwie w każdym systemie liczbowym. Wystarczy zamiast potęg dwójki wpisywać kolejne potęgi podstawy systemu.
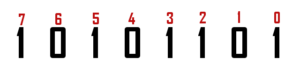
Listę powyższych kroków możemy uogólnić i przedstawić na schemacie blokowym:
System binarny na dziesiętny — implementacje
W przypadku programów komputerowych konwersja ta zachodzi podobnie, jak byśmy robili to na kartce papieru. Oczywiście istnieją biblioteki pozwalające na szybką zamianę liczb, ale na maturze możemy nie mieć do nich dostępu. W związku z tym poniżej znajdziesz implementacje w C++, Javie oraz Pythonie:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
//program konwertujący liczbę zapisaną dwójkowo na sytem dziesiętny //Łukasz Kosiński #include <iostream> #include <cmath> using namespace std; int konwersja(const string &a) { int wynik=0; for(int i=0; i<a.length(); i++) wynik+=(a[i]-'0')*pow(2, a.length()-1-i);//0 lub 1 jest mnożone przez potęgę dwójki i dodawane do wyniku //a[i] jest typu char, aby uzyskać 1 lub 0 odejmujemy od wartości tego elementu kod ACII znaku '0', czyli 48 //kod ACII dla 0 to 48, więc 48-48 daje 0 //kod ACII dla 1 to 49, więc 49-48 daje 0 return wynik; } int main() { string binarnie; cin >> binarnie; int dziesietnie=konwersja(binarnie); cout << dziesietnie << endl; return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
import java.util.Scanner; public class binary_to_decimal { public static void main(String[] args) { System.out.println("Program konwertujacy liczbe w systemie binarnym, na liczbe w systemie dziesietnym"); System.out.println("Podaj liczbę zapisaną w systemie binarnym: "); Scanner scanner = new Scanner(System.in); // inicjalizacja skanera, który będzie pobierał wartości zmiennych String binary = scanner.nextLine(); // pobieramy liczbe binarna od uzytkownika int dec = 0; for(int i = binary.length() - 1; i >= 0; i --) { //iterujemy poprzez wartosc binarna (zapisana w string), pamietaj jednak, że nalezy to robić od końca int n = binary.charAt(i) - '0'; //konwersja char'a na int - '6' jako char, to nie to samo co 6 jako int, chary reprezentują index z tablicy ASCII, dlatego należy od nich odjąć wartość dla chara '0' dec += Math.pow(2, (binary.length() - 1 - i)) * n; // dodajemy odpowiednią potęgę dwójki, pomnożoną przez aktualną pozycje w liczbie binarnej (1 lub 0) } System.out.println("Liczba dziesiętna to: " + dec); scanner.close(); // zwalniamy zasoby } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 |
def dziesietna(x): #definiujemy funkcje do późniejszego użycia i = len(x) - 1 # zapisujemy zmienna iteracyjna potrzebna do okreslenia potegi dwojek dec = 0 # zmienna pomocnicza przechowujaca finalny wynik for c in x: #iterujemy poprzez kazda cyfre od lewej dec += int(c) * pow(2, i); #dodajemy odpowiednia wartosc i -= 1 #jednoczesnie zmniejszajac wartosc zmiennej iteracyjnej return dec print("Program konwertujacy liczbe binarna na dziesietna") print("Podaj liczbę binarna a: ") a = input() print(dziesietna(a)) |
Jak zamieniać liczby dziesiętne na binarne?
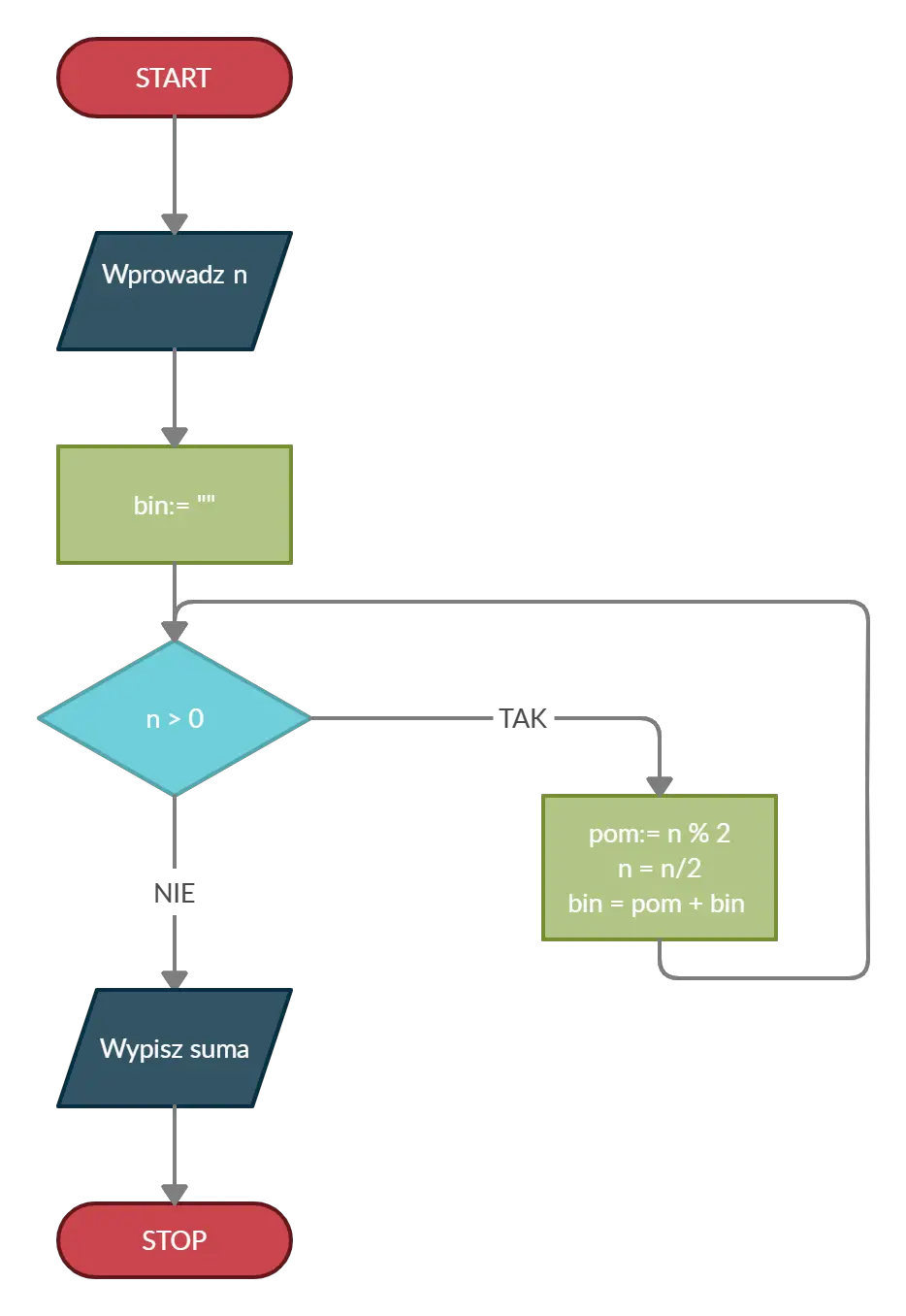
Skoro umiemy już zamienić liczbę binarną na dziesiętną, musimy jeszcze prześledzić jak zrobić to w drugą stronę. Zamiana polega na ciągłym dzieleniu całkowitym liczby na dwa i zapisywaniu reszty z dzielenia. Następnie reszty z dzielenia wypisujemy od końca, w wyniku czego otrzymamy liczbę w systemie binarnym. Weźmy znowu pod lupę liczbę z poprzedniego przykładu: 20:
- Dzielimy 20 na 2, czego wynikiem jest 10. Reszta z tego dzielenia jest równa 0.
- Dzielimy 10 na 2, czego wynikiem jest 5. Reszta z dzielenia jest równa 0.
- Dzielimy 5 na 2, czego wynikiem jest 2(pamiętaj, że dzielimy całkowicie, czyli pomijamy rozwinięcie dziesiętne). Reszta z tego dzielenia jest równa 1.
- Dzielimy 2 przez 2, czego wynikiem jest 1. Reszta z dzielenia równa 0.
- Dzielimy 1 przez 2: wynik równy 0. Reszta z dzielenia: 1.
- Bierzemy teraz wszystko do kupy, zaczynając od końca: 10100 — oto nasza liczba w systemie binarnym.
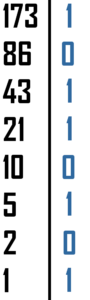
Wszystkie powyższe kroki przedstawiłem na poniższym schemacie blokowym. Wykorzystałem w nim operator modulo(%), który zwraca resztę z dzielenia dwóch liczb.
System binarny — konwersja z dziesiętnego implementacje
Wiedząc już, jak zamienić liczbę dziesiętną na binarną, nie pozostało nam nic innego, jak wdrożyć tą wiedzę w program. Poniżej znajdziesz implementacje w językach dostępnych na maturze z informatyki.
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
//program konwertujący liczbę zapisaną dziesiętnie na system dwójkowy //Łukasz Kosiński #include <iostream> #include <algorithm> using namespace std; void konwersja(int a, string &b)//funkcja działa na oryginale przekazywanego do niej stringa { for(; a>=1; a/=2)//po każdym wykonaniu pętli liczba jest dzielona przez 2 bez reszty, dopóki będzie nie mneijsza od 1 { if(a%2==0)//jeśli reszta z dzielenia liczby przez 2 wynosi 0 to dodajemy do stringa '0' b.push_back('0');//metoda .push_back() dodaje na końcu stringa znak, bądź cały łańcuch else//w przeciwnym wypadku dodajemy '1' b.push_back('1'); } reverse(b.begin(), b.end());//odwracamy stringa } int main() { int dziesietnie; cin >> dziesietnie; string binarnie; konwersja(dziesietnie, binarnie); cout << binarnie; return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import java.util.Scanner; public class decimal_to_binary { public static void main(String[] args) { System.out.println("Program konwertujacy liczbe w systemie dziesietnym, na liczbe w systemie binarnym"); System.out.println("Podaj liczbę zapisaną w systemie dziesietnym: "); Scanner scanner = new Scanner(System.in); // inicjalizacja skanera, który będzie pobierał wartości zmiennych int n = scanner.nextInt(); // pobieramy liczbe dziesietna od uzytkownika String bin = ""; // tworzymy zmienne pomocnicze int p = n; while(p != 0) { bin = p % 2 + bin; // zapisujemy modulo z dzielenia przez 2 (albo 0, albo 1), pamiejąc, że taka liczba jest tworzona od końca p /= 2; // dzielimy zmienną pomocniczą przez 2 } System.out.println("Liczba binarna to: " + bin); scanner.close(); // zwalniamy zasoby } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
def binarna(x): #definiujemy funkcje do późniejszego użycia if x == 0: #jezeli liczba jest 0 return "0" # zwroc od razu wynik b = "" # w przeciwnym wypadku tworzymy zmienna pomocnicza przechowujaca liczbe binarna jako tekst while x != 0: #dopoki nasza dziesietna liczba nie bedzie rowna 0 b = str(x % 2) + b #dodaj do pomocniczej reszte z dzielenia przez 2 x = int(x/2) # a nastepnie podziel calkowicie (bez reszty) przez 2 return b #na koniec zwracamy finalna zmienna print("Program konwertujacy liczbe dziesietna na binarna") print("Podaj liczbę a: ") a = int(input()) print(binarna(a)) |
Podsumowanie
Jak wspominałem na początku, system binarny jest nieodłączną częścią matury z informatyki. Aby ją jak najlepiej napisać warto więc mieć go małym palcu. Jeżeli szukasz dodatkowych materiałów do nauki, zajrzyj do tego wpisu. Omówiłem tam najważniejsze, przydatne na maturze rzeczy. Znajdziesz tam również listę wartych uwagi algorytmów.







Kaleron
says:W praktyce o wiele częściej posługujemy się systemem szesnastkowym. Ma on te zalety, że jego podstawa jest potęgą dwójki, a zapisywane w nim liczby są dużo łatwiejsze od odczytywania, gdyż mają 4 razy mniej cyfr, niż w przypadku systemu dwójkowego. W dodatku mamy szesnaście cyfr, przez co rzadziej występują długie ciągi powtarzalnych symboli (czytając długi ciąg złożony wyłącznie z cyfr 0 i 1 bardzo łatwo się pomylić, czytając choćby i równie długi, ale bardziej zróżnicowany ciąg cyfr szesnastkowych pomylić się o wiele trudniej), a jednocześnie lest to liczba cyfr nadal łatwa do zapamiętania. Dla początkujących trudnością jest przyzwyczaić się, że A, to dziesiątkowe 10, a nie 11, a F, to dziesiątkowe 15, a nie 16. Tak nam podpowiada intunicja wykorzystująca naszą wiedzę o tym, że A jest pierwszą literą alfabetu, a F – szóstą, ale jeśli ponumerujemy je od zera….numerowanie od zera nie powinno być dużą niespodzianką dla osób zainteresowanych informatyką.
System szesnastkowy przydaje się w wielu dziedzinach, jak np. w odzyskiwaniu danych, czy w niskopoziomowej analizie oprogramowania, gdzie często pracujemy z plikami binarnymi w hex-edytorze. Ale czym innym jest patrzeć na hexy, a czym innym jest je analizować i przeliczać. Tak, zawsze możemy przeliczać wszystkie wartości szesnastkowe na dziesiątkowe, wykonywać obliczenia w systemie dziesiątkowym i przeliczać wynik na system szesnastkowy, tylko po co? przecież to tylko dodatkowa praca i dodatkowa okazja, by się pomylić. A przecież matematyka jest zawsze taka sama i nie zalezy od wybranej przez nas podstawy systemu liczbowego. Dlatego przygotowałem szesnastkową tabliczkę mnożenia:
http://kaleron.pl/tabliczka-mnozenia.htm