Na łamach blogu często pojawiało się wyrażenie „złożoność obliczeniowa” – zwłaszcza przy algorytmach sortujących. Określeniu temu towarzyszył, zazwyczaj, z pozoru dziwny wzór przy literce O. Jest to istotne zagadnienie, które jest przydatne na maturze z informatyki. Omówimy więc dzisiaj czym jest złożoność obliczeniowa, a także w jaki sposób możemy ją wyrażać.
Pojęcie złożoności
Zanim przejdziemy do złożoności obliczeniowej, warto najpierw wyjaśnić, czym jest sama złożoność. Odkąd komputery istniały, potrzeba było sposobu na określenie zasobów potrzebnych do wykonania programu. Było to szczególnie ważne, gdyż dawniej urządzenia miały ograniczoną moc obliczeniową – wielokrotnie niższą niż dzisiejsze smartfony. Aby uprać się z tym problemem powstały takie pojęcia, jak złożoność obliczeniowa, która określa ilość operacji wymaganych do wykonania całego programu, czy złożoność pamięciowa, która określa ilość pamięci operacyjnej wymaganej do wykonania programu.
Ale po co się martwić?
A no trzeba się martwić – gdy algorytm wykonujący 1000 operacji zostanie uruchomiony 10^7 razy, to zapewniam Cię, że zauważysz jak wolno on działa :). Innymi słowy, pojedyncze uruchomienie algorytmu o wysokiej złożoności obliczeniowej nie spowoduje zauważalnego spadku wydajności programu, jednak jego implementacja w projektach przetwarzających duże ilości danych będzie już odczuwalna. Krócej mówiąc: optymalizacja tego wymaga, moi drodzy.
Jak obliczyć złożoność obliczeniową algorytmu?
Aby określić złożoność obliczeniową algorytmu, musimy zliczyć ilość wykonywanych przez niego operacji. Za pojedynczą operację uznajemy każdą, prostą instrukcję jak inicjalizacja zmiennej, wykonanie działania, czy zwrócenie wyniku metody. Przyjmijmy że f(n) to funkcja zwracająca ilość operacji, w zależności od ilości wprowadzanych danych n. Spójrzmy na poniższe przykłady:
C++
|
1 2 3 |
void wypisz(int n){ std::cout << "Wykonałem operacje wypisania tekstu!"; } |
Java
|
1 2 3 |
void wypisz(int n) { System.out.println("Wykonałem operacje wypisania tekstu!"); } |
Python
|
1 2 |
def wypisz(n): print("Wykonałem operacje wypisania tekstu!") |
Powyższe funkcje wykonują dokładnie jedną operację. Oznacza to, że ich złożoność obliczeniową możemy wyrazić jako f(n) = 1 (niezależnie od n funkcja print zawsze wykona się raz).
C++
|
1 2 3 4 5 6 |
void wypisz(int n) { for (int i = 1; i <= n; i++) { std::cout << "Wykonałem operacje po raz " << i; } std::cout << "Wykonałem kolejną operację!"; } |
Java
|
1 2 3 4 5 6 |
void wypisz(int n) { for (int i = 1; i <= n; i++) { System.out.println("Wykonałem operacje po raz " + i); } System.out.println("Wykonałem kolejną operację!"); } |
Python
|
1 2 3 4 |
def wypisz(n): for i in range(1, n+1): print("Wykonałem operacje po raz ", i) print("Wykonałem kolejną operację!") |
Funkcja wypisz wywołuje teraz pętlę, która iteruje n razy. Następnie wykonujemy jeszcze jedną operację poza pętlą. Oznacza to, że nasz algorytm jest teraz zależny od wprowadzonych danych. Jego złożoność obliczeniową możemy więc wyrazić jako f(n) = n + 1.
Idąc tym samym tokiem rozumowania, możemy wyznaczyć ilość wykonywanych operacji dla nieco bardziej skomplikowanych algorytmów. Przyjrzyj się poniższym przykładom:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
void wypisz(int n) { for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { for (int k = 1; k <= n; k++) { std::cout << "Wykonałem operacje w pierwszej pętli"; } std::cout << "Wykonałem operacje w drugiej pętli"; std::cout << "Wykonałem kolejną operacje w drugiej pętli"; } std::cout << "Wykonałem operacje w trzeciej pętli"; std::cout << "Wykonałem kolejną operacje w trzeciej pętli"; std::cout << "Wykonałem kolejną operacje w trzeciej pętli"; } std::cout << "Wykonałem operację poza pętlą"; std::cout << "Wykonałem operację poza pętlą"; std::cout << "Wykonałem operację poza pętlą"; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
void wypisz(int n) { for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { for (int k = 1; k <= n; k++) { System.out.println("Wykonałem operacje w pierwszej pętli"); } System.out.println("Wykonałem operacje w drugiej pętli"); System.out.println("Wykonałem kolejną operacje w drugiej pętli"); } System.out.println("Wykonałem operacje w trzeciej pętli"); System.out.println("Wykonałem kolejną operacje w trzeciej pętli"); System.out.println("Wykonałem kolejną operacje w trzeciej pętli"); } System.out.println("Wykonałem operację poza pętlą"); System.out.println("Wykonałem operację poza pętlą"); System.out.println("Wykonałem operację poza pętlą"); } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
def wypisz(n): for i in range(n): for j in range(n): for k in range(n): print("Wykonałem operacje w pierwszej pętli") print("Wykonałem operacje w drugiej pętli") print("Wykonałem ostatnią operację w drugiej pętli") print("Wykonałem operacje w trzeciej pętli") print("Wykonałem jeszcze jedną operacje w trzeciej pętli") print("Wykonałem ostatnią operację w trzeciej pętli") print("Wykonałem kolejną operację poza pętlą") print("Wykonałem jeszcze jedną operację poza pętlą") print("Wykonałem ostatnią operację poza pętlą") |
Powyższy program wydrukuje tekst w konsoli n3+2n2+3n+3 razy – jego dokładna złożoność będzie określona więc funkcją f(n) = n3+2n2+3n+3.
W informatyce jednak rzadko kiedy wyznacza się dokładną złożoność obliczeniową. Zamiast tego korzysta się z oszacowań – tzw. notacji O (wielkiego O), Ω(omegi), bądź Θ(theta).

Notacja O
Najczęściej używana notacja, w której złożoność obliczeniowa jest oszacowywana z góry. Notacja ta jest zgodna z poniższym wzorem:
f(n) = O(g(n))
Oznacza on, że dla dowolnego n istnieje takie n0, dla którego spełniona jest nierówność f(n)<c*g(n). Funkcja f(n) jest co najwyżej rzędu funkcji g(c). Liczba c we wzorze jest pewną, stałą liczbą. Weźmy pod lupę powyższą funkcję f(n) = n3+2n2+3n+3. W notacji wielkiego O pod uwagę bierzemy tylko najistotniejszy wyraz (zazwyczaj z największą potęgą). Szacując złożoność odrzucamy również współczynniki przy wyrazach. Sprawdźmy więc, który wyraz ma największy wpływ na wartość funkcji dla wystarczająco dużego argumentu, np. 10000:
| Wyraz | Wartość |
| n3=100003 | 1000000000000 |
| n2=100002 | 100000000 |
| n=10000 | 10000 |
| 3 | 3 |
Wartość wyrazu n3 wzrasta zdecydowanie szybciej od pozostałych, mając coraz to większy wpływ na finalną wartość złożoności obliczeniowej. Oznacza to, że wraz ze wzrostem ilości wprowadzanych danych złożoność obliczeniowa będzie zbliżać się do wartości n3 – dlatego funkcja f(n) ma złożoność O(n3).
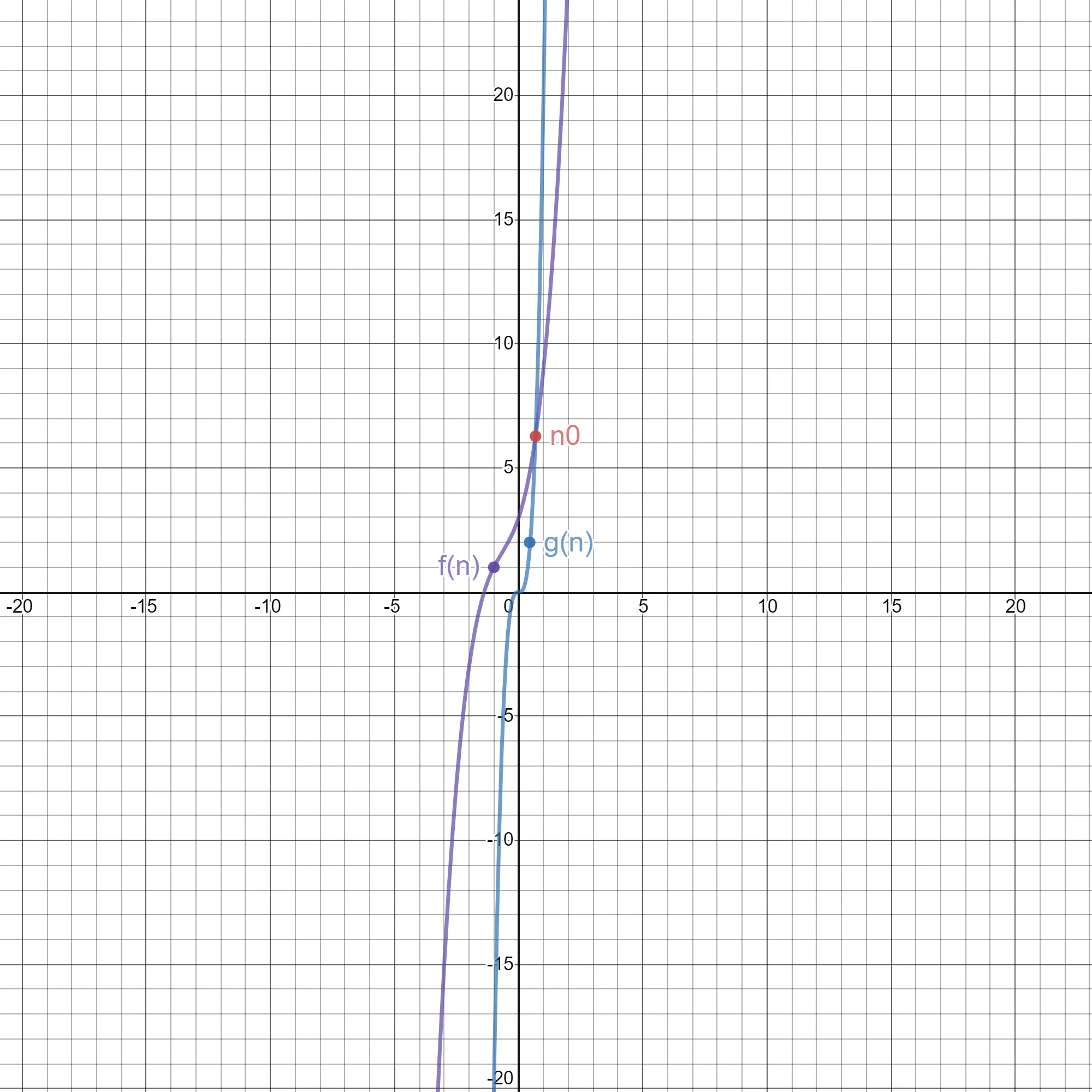
Zwróć uwagę, że jest to tylko oszacowanie. Dla funkcji f(n)=2n+5 oszacowanie O(n^6), będzie jak najbardziej poprawne, aczkolwiek mało precyzyjne.
Notacja Ω
Notacja omega jest przeciwieństwem notacji wielkiego O. Wzór:
f(n)=Ω(g(c))
jest prawdziwy, gdy istnieje takie n0, od którego wartość f(n) jest większa od c*g(n). W tym przypadku funkcja f(n) jest co najmniej rzędu funkcji g(n). Dokonujemy więc tu dolnego oszacowania funkcji f(n). Podobnie jak poprzednio nie interesują nas współczynniki stojące przy wyrazach funkcji. Oszacowanie naszej funkcji f(n)=n3+2n2+3n+3 będzie więc wynosiło Ω(n2).
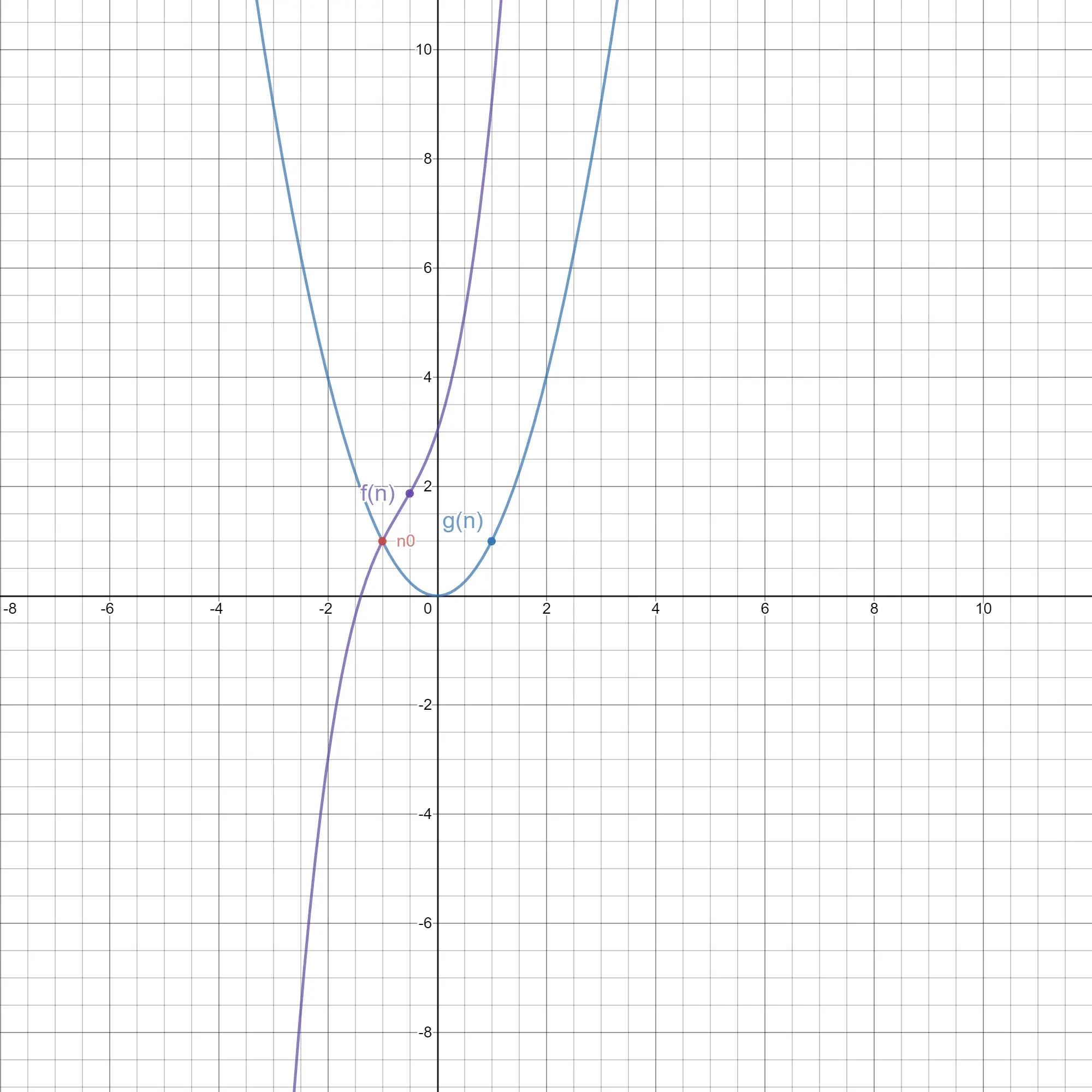
Ponownie zwracam uwagę, iż jest to jedynie oszacowanie. Moglibyśmy tutaj podać nawet Ω(n), jednak ponownie, będzie to mało precyzyjne.
Notacja Θ
Notację theta można właściwie traktować jako pewnego rodzaju ciekawostkę. Jest ona połączeniem notacji wielkiego O i omegi. Wzór:
f(n) = Θ(g(n))
jest prawdziwy, gdy c1 * g(n) < f(n) < c2 * g(n). Wyrazy c1 i c2 to pewne, stałe liczby. Wydawać by się mogło, że notacja ta oszacuje najprecyzyjniej złożoność obliczeniową, jednak nie przewiduje ona sytuacji optymistycznych, przez co nieraz oszacowanie może być błędne. Przykładem notacji theta dla naszej funkcji może być Θ(n2):
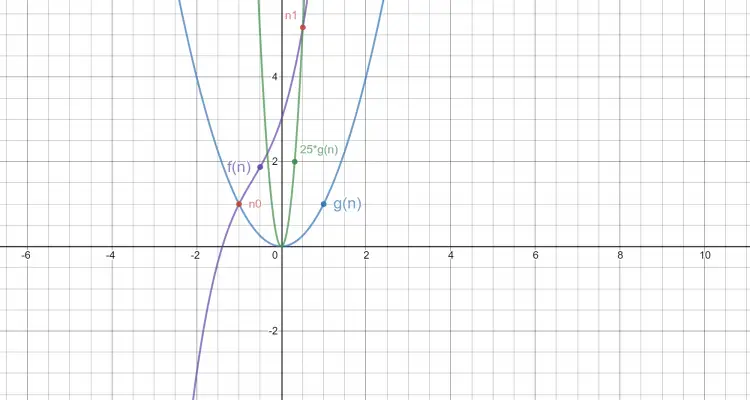
Złożoność obliczeniowa – przykłady
Pokażemy teraz przykładowe algorytmy i ich złożoności obliczeniowe, za pomocą notacji wielkiego O.
Stała złożoność obliczeniowa O(1)
Przykład stałej złożoności obliczeniowej pokazaliśmy już dzisiaj przy pierwszym przykładzie. W praktyce złożoność taką osiągają jedynie funkcje, mające za zadanie jedynie zwrócenie pojedynczej wartości.
Liniowa złożoność obliczeniowa O(n)
Program osiąga złożoność O(n), gdy ilość wykonywanych operacji jest wprost proporcjonalna do ilości wprowadzanych danych. Złożoność taką osiągają np. programy mające za zadanie wyszukanie najmniejszego elementu w tablicy:
C++
|
1 2 3 4 5 6 7 8 9 10 11 |
#include <iostream> #include <limits> int wypisz(int* tablica, int n) { int min = std::numeric_limits<int>::max(); //maksymalna wartosc calkowita for(int i = 0; i<n; i++) { if(tablica[i] < min) { min = tablica[i]; } } return min; } |
Java
|
1 2 3 4 5 6 7 8 9 |
int wypisz(int[] tablica) { int min = Integer.MAX_VALUE; for(int i = 0; i<tablica.length(); i++) { if(tablica[i] < min) { min = tablica[i]; } } return min; } |
Python
|
1 2 3 4 5 6 7 |
import sys def wypisz(tablica): min = sys.maxsize for i in range(len(tablica)): if tablica[i] < min: min = tablica[i] return min |
Kwadratowa złożoność obliczeniowa O(n2)
Kwadratowa złożoność osiągana jest poprzez zagnieżdżenie pętli w pętli. Zabieg taki spotykamy w, owianym złą sławą, algorytmie sortowania bąbelkowego. Przeczytać możesz o nim tutaj. Złożoność O(n2) ma również algorytm sortowania przez wstawianie.
Logarytmiczna złożoność obliczeniowa O(log(n))
Algorytmy o złożoności logarytmicznej są z jednymi z szybszych. Złożoność taka osiągana jest zazwyczaj poprzez dzielenie zadania na mniejsze części, jak ma to np. miejsce w wyszukiwaniu binarnym. Logarytmiczną złożoność obliczeniową osiąga również algorytm sortowania przez scalanie.
Pierwiastkowa złożoność obliczeniowa O(√n)
Podobnie jak w przypadku logarytmicznej złożoności, algorytmy bazujące na pierwiastkowej są uznawane za dosyć szybkie. Złożoność pierwiastkowa osiągana jest zazwyczaj w wyniku pojedynczej iteracji do pierwiastka z n. Przykładem takiego algorytmu jest sprawdzanie, czy liczba jest pierwsza.
Podsumowanie
Jak pewnie sami zauważyliście, złożoność obliczeniowa gra ważną rolę w optymalizacji programów. Niejednokrotnie jej zastosowanie pojawiało się również na maturze z informatyki. Jeżeli więc chcesz się do niej jak najlepiej przygotować, zajrzyj koniecznie do tego wpisu.





