Ideą serii wpisów o podstawowych algorytmach jest podzielenie się z młodymi programistami (w tym przede wszystkim maturzystami) moimi implementacjami popularnych programów, wykorzystujących właśnie te algorytmy — w końcu nic tak nie szlifuje wiedzy, jak wykorzystanie jej w praktyce. Znajomość tych algorytmów jest istotna na maturze z informatyki, gdyż niektóre zadania zabraniają użycia wbudowanych metod. Przykładem jest algorytm sortowania — jesteśmy wtedy zmuszeni stworzyć go samodzielnie. Jednym z najbardziej podstawowych algorytmów jest ten, który z wyznacza dzielniki liczby naturalnej.
Za dzielnik liczby n uznajemy dowolną liczbę naturalną k, która dzieli liczbę n bez reszty. Dla przykładu dzielnikami liczby 24 są 1, 2, 3, 4, 6, 8, 12 i 24. Zauważ, że dla każdej liczby n ilość dzielników jest zawsze parzysta, a w nich zawsze znajdzie się 1 i n. Liczby, które posiadają jedynie dwa dzielniki: 1 i siebie samą, nazywamy liczbami pierwszymi, o których dowiesz się więcej tutaj. Jak znaleźć dzielniki liczby? Musimy najpierw ustalić algorytm, według którego będziemy działać, a następnie zaimplementujemy go w Javie, C++ i Pythonie.
Algorytm znajdowania dzielników liczby
Na początku musimy ustalić pewną liczbę naturalną n. Aby znaleźć jej wszystkie dzielniki, najprościej będzie sprawdzić po kolei reszty z dzielenia przez wszystkie liczby mniejsze lub równe jej połowie, wiadomo przecież, że dzielenie liczby przez więcej niż jej połowę nigdy nie da całkowitego wyniku. Do tej operacji wykorzystamy pętle oraz operator modulo (%), który zwraca resztę z dzielenia dwóch liczb. Na początku algorytmu wypisujemy 1 — jest to dzielnik każdej liczby. Następnie sprawdzamy wszystkie liczby z przedziału <2, (n/2)> za pomocą operatora modulo — jeżeli reszta z dzielenia będzie równa 0, wypisujemy iterowaną liczbę jako dzielnik. Na koniec algorytmu wypisujemy liczbę n — ona też jest swoim własnym dzielnikiem. Algorytm jest prosty w działaniu i nie pochłania wielu zasobów, a jego schemat blokowy możesz przeanalizować poniżej:
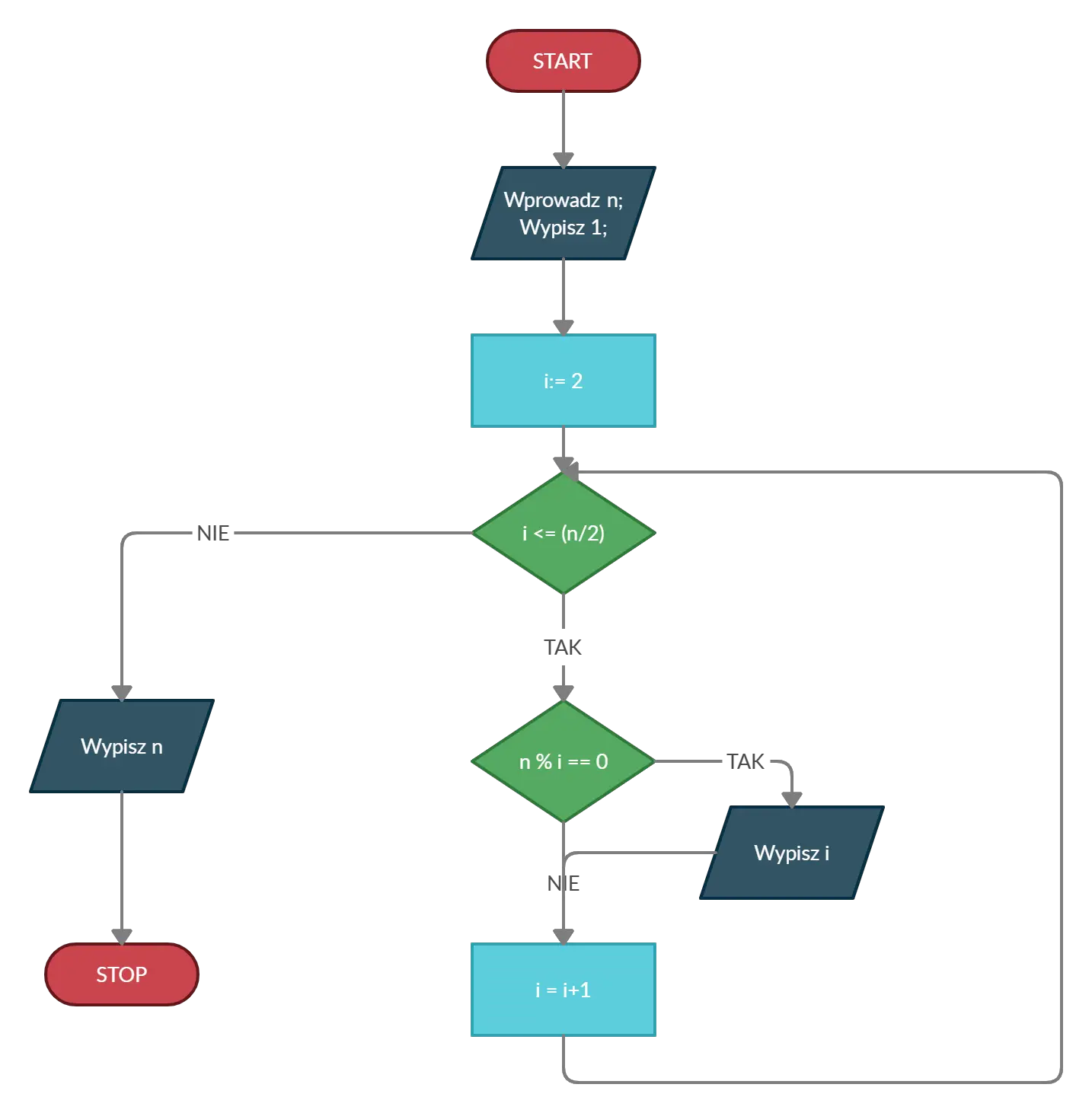
Dzielniki liczby — implementacja Java, C++, Python
Jak już wspominałem na początku, znajomość podstawowych algorytmów jest wręcz wymagana na maturze z informatyki. Dobrze by było również wiedzieć jak je użyć w praktyce, dlatego, jak w każdym ze wpisów o algorytmach, poniżej umieszczam implementacje algorytmu. Ponieważ post ten kierowany jest głównie do osób przygotowujących się do matury, implementacje te napisane są w trzech dostępnych na maturze językach programowania: Javie, C++ i Pythonie.
Dzielniki liczby – implementacja C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
//program wypisujący dzielniki danej liczby //Kosiński Łukasz #include <iostream> using namespace std; void dzielniki(unsigned a) { cout << "Dzielniki liczby " << a << " to: 1, "; //wypisujemy od razu jedynke for(int i=2; i<=(a/2); i++) { if(a%i==0) {//funkcja wypisuje daną liczbę jeśli dzieli argument bez reszty cout << i << ", "; } } std::cout << a << ";" << endl; //na koniec wypisujemy rowniez wprowadzona liczbe - ona tez jest swoim dzielnikiem } int main() { unsigned x; cin >> x; dzielniki(x); return 0; } |
Dzielniki liczby – implementacja Python
|
1 2 3 4 5 6 7 8 9 10 11 |
def dzielniki(x): #definiujemy funkcje do późniejszego użycia for i in range(1, int(x/2) + 1): # iterujemy od jedynki, do polowy liczby x - dzielenie przez wiecej niz polowe nie da calkowitego wyniku if x % i == 0: #jezeli liczba i jest dzielnikiem liczby x print(str(i) + " "), #wypisz ja print(x), #na koniec wypisujemy liczbe x - ona tez jest swoim dzielnikiem print("Program znajdujacy dzielniki liczby") print("Podaj liczbę: ") a = int(input()) dzielniki(a) |
Dzielniki liczby – implementacja Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
package matura; import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner s = new Scanner(System.in); int liczba = s.nextInt(); System.out.print("Dzielniki liczby " + liczba + " to: 1, "); //wypisujemy od razu jedynke for(int i=2;i<=(liczba/2);i++){ //iterujemy do polowy wprowadzonej liczby if((liczba % i)==0) {//Jeśli reszta dzielenia liczby przez i wynosi 0 to jest to dzielnik i go wy[isujemy] System.out.print(i + ", "); } } System.out.print(liczba + ";"); //na koniec wypisujemy rowniez wprowadzona liczbe - ona tez jest swoim dzielnikiem s.close(); //zwalniamy zasoby } } |





