Pomimo panującej pandemii, dla większości uczniów rok szkolny ruszył już pełną parą, choć przez obowiązujące obostrzenia i przepisy nie było to łatwe. Ten trudny okres daje się na pewno we znaki maturzystom – w końcu kilkumiesięczna przerwa od nauki nie idzie w parze z dobrym przygotowaniem do matury, a przecież każdy chciałby osiągnąć jak najlepszy wynik. Matura z informatyki 2019 rozwiązania to wpis, który pomoże wam w osiągnięciu tego celu.
Matura z informatyki 2019 — część pierwsza (teoria)
Tak jak co roku egzamin dojrzałości z informatyki został podzielony na dwa arkusze — część teoretyczną i część praktyczną. Standardowo w obu znajdziemy po 3 zadania o zróżnicowanej ilości podpunktów i ich trudności, a na ich wykonanie było 60 minut. Nie owijając dalej w bawełnę, przejdźmy do rozwiązywania zadań:
Matura z informatyki 2019: Zadanie 1 — ulubione liczby

Z treści zadania możemy już wywnioskować, że operować będziemy na zbiorze liczb, w którym na początku znajdziemy same liczby nieparzyste, a następnie do samego końca liczby parzyste. Jak zdefiniować liczby parzyste/nieparzyste? Liczba rzeczywista n jest liczbą nieparzystą, gdy reszta z dzielenia n/2 jest różna od 0, zaś gdy ta reszta będzie równa 0, to n jest liczbą parzystą. W większości języków programowania do obliczania reszty z dzielenia służy operator modulo (symbol %) — przyda nam się on w tym zadaniu.
Zadanie 1 — podpunkt 1

Podpunkt ten można rozwiązać na kilka sposobów. Poniżej znajdziesz rozwiązania w C++, Pythonie i Javie — trzech językach, które możesz wybrać na maturze z informatyki. Użyjemy również podanego przez CKE przykładowego zestawu danych, aby sprawdzić poprawność działania programu.
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
#include <iostream> using namespace std; int pierwszaParzysta(int* A, int n){ for(int i = 0; i < n; i++){ // petla iterujaca przez elementy zbioru A if(A[i] % 2 == 0){ // jezeli iterowany element jest podzielny przez 2 (reszta z dzielenia przez 2 jest rowna 0) return A[i]; // zwroc ta liczbe i przerwi petle } } } int main(){ int A[10] = {5, 99, 3, 7, 111, 13, 4, 24, 4, 8}; // tworzymy zmienne int n = 10; // z danymi z przykladu int w = pierwszaParzysta(A, n); // wywolujemy nasza funkcje cout << w << " jest pierwsza liczba wypisana przez Jasia"; //a nastepnie drukujemy jej wynik w konsoli return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
package matura; import java.io.IOException; public class Main { static int pierwszaParzysta(int[] A, int n){ //definiujemy oddzielna, uniwersalna funkcje for(int i = 0; i < n; i++){ // petla iterujaca przez elementy zbioru A if(A[i] % 2 == 0){ // jezeli iterowany element jest podzielny przez 2 (reszta z dzielenia przez 2 jest rowna 0) return A[i]; // zwroc ta liczbe i przerwi petle } } return 0; //jezeli nie znajdziemy liczby parzystej zwracamy 0 //co prawda jest to niemozliwe, ale dla spojnosci i logiki kodu nalezy poza petla zwrocic jakas wartosc } public static void main(String[] args) throws IOException { int[] A = {5, 99, 3, 7, 111, 13, 4, 24, 4, 8}; // tworzymy zmienne int n = 10; // z danymi z przykladu int w = pierwszaParzysta(A, n); // wywolujemy nasza funkcje System.out.println(w + " jest pierwsza liczba wypisana przez Jasia"); //a nastepnie drukujemy jej wynik w konsoli } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 |
def pierwszaParzysta(A, n): #definiujemy funkcje wyszukujaca pierwsza liczbe parzysta w zbiorze for i in range(n): #iterujemy przez tablice o wielkosci n if A[i] % 2 == 0: #jezeli natrafimy na pierwsza liczbe parzysta return A[i] #zwracamy ja return None #jezeli nie znajdziemy liczby parzystej zwracamy None #co prawda jest to niemozliwe, ale dla spojnosci i logiki kodu nalezy poza petla zwrocic jakas wartosc tablica = [5, 99, 3, 7, 111, 13, 4, 24, 4, 8] #tworzymy zmienne wielkosc = 10 #z danymi z przykładu pierwsza = pierwszaParzysta(tablica, wielkosc) #wywołujemy naszą funkcję print(str(pierwsza) + " jest pierwsza liczba wypisana przez Jasia") #a następnie drukujemy jej wynik w konsoli |
Sposób ten, choć jest sam w sobie prawidłowy i najprostszy, nie uzyska maksymalnej ilości punktów. Dlaczego? Jego złożoność obliczeniowa jest liniowa, a z treści zadania wyczytać można, że aby uzyskać maksymalną ilość punktów, złożoność powinna być lepsza niż liniowa. W związku z tym przedstawiam drugi sposób:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
#include <iostream> using namespace std; int pierwszaParzysta(int* A, int n) { int i = 0; //inicjalizacja zmiennej przechowującej index 'najnizszego' elementu int m = n-1; //inicjalizacja zmiennej przechowujacej index 'najwyzszego' elementu while(i < m){ //wyszukiwanie binarne - wykorzystujemy w tym celu petle while int s = (i+m)/2; //inicjalizacja zmiennej przechowujacej index 'srodkowego' elementu if(A[s] % 2 == 0){ //jezeli element ten jest podzielny przez 2(reszta z dzielenia przez 2 jest rowna 0) m = s; // kończymy dzialanie petli zapisujac index podanego elementu } else{ i=s+1; //w przeciwnym wypadku zwiekszamy index 'najnizszego' elementu kontynuujac petle } } return A[m]; //zwracamy otrzymana liczbe } int main(){ int A[10] = {5, 99, 3, 7, 111, 13, 4, 24, 4, 8}; // tworzymy zmienne int n = 10; // z danymi z przykladu int w = pierwszaParzysta(A, n); // wywolujemy nasza funkcje cout << w << " jest pierwsza liczba wypisana przez Jasia"; //a nastepnie drukujemy jej wynik w konsoli return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
package matura; import java.io.IOException; public class Main { static int pierwszaParzysta(int[] A, int n) { //definiujemy oddzielna, uniwersalna funkcje int i = 0; //inicjalizacja zmiennej przechowujacej index 'najnizszego' elementu int m = n - 1; //inicjalizacja zmiennej przechowujacej index 'najwyzszego' elementu while (i < m) { //wyszukiwanie binarne - wykorzystujemy w tym celu petle while int s = (i + m) / 2; //inicjalizacja zmiennej przechowujacej index 'srodkowego' elementu if (A[s] % 2 == 0) { //jezeli element ten jest podzielny przez 2(reszta z dzielenia przez 2 jest rowna 0) m = s; // zakanczamy dzialanie petli zapisujac index pozadanego elementu } else { i = s + 1; //w przeciwnym wypadku zwiekszamy index 'najnizszego' elementu kontynuujac petle } } return A[m]; //zwracamy otrzymana liczbe } public static void main(String[] args) throws IOException { int[] A = {5, 99, 3, 7, 111, 13, 4, 24, 4, 8}; // tworzymy zmienne int n = 10; // z danymi z przykladu int w = pierwszaParzysta(A, n); // wywolujemy nasza funkcje System.out.println(w + " jest pierwsza liczba wypisana przez Jasia"); //a nastepnie drukujemy jej wynik w konsoli } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
def pierwszaParzysta(A, n): #definiujemy funkcje wyszukujaca pierwsza liczbe parzysta w zbiorze i = 0 #inicjalizacja zmiennej przechowującej index 'najniższego' elementu m = n-1 #inicjalizacja zmiennej przechowujacej index 'najwyższego' elementu while i < m: #wyszukiwanie binarne - wykorzystujemy w tym celu petle while s = int((i+m)/2) #inicjalizacja zmiennej przechowujacej index 'środkowego' elementu if A[s] % 2 == 0: #jezeli element ten jest podzielny przez 2(reszta z dzielenia przez 2 jest równa 0) m = s #zakańczamy działanie pętli zapisując index pożądanego elementu else: i = s+1 #w przeciwnym wypadku zwiększamy index 'najnizszego' elementu kontynuujac petle return A[m] #zwracamy otrzymana liczbe tablica = [5, 99, 3, 7, 111, 13, 4, 24, 4, 8] #tworzymy zmienne wielkosc = 10 #z danymi z przykładu pierwsza = pierwszaParzysta(tablica, wielkosc) #wywołujemy naszą funkcję print(str(pierwsza) + " jest pierwsza liczba wypisana przez Jasia") #a następnie drukujemy jej wynik w konsoli |
W powyższych kodach wykorzystaliśmy wyszukiwanie binarne, co dało nam logarytmiczną złożoność obliczeniową, a więc lepszą od liniowej. Zwracam uwagę, że w tym podpunkcie można było wykorzystać inne algorytmy o złożoności lepszej niż liniowa, np. o podanej w kluczu przez CKE złożoności pierwiastkowej.
Zadanie 1 — podpunkt 2

Rozwiązanie zależy od wybranego wcześniej sposobu. Preferowanym przeze mnie sposobem jest ten wykorzystujący wyszukiwanie binarne — w tym przypadku odpowiedzią będzie złożoność logarytmiczna.
Matura z informatyki 2019: Zadanie 2 – algorytm

Przeanalizujmy krok po kroku działanie tego algorytmu:
- Użytkownik wprowadza 3 zmienne: napis s, liczbę n (większa/równa od dł(s)) oraz liczbę k ze zbioru {2, 3, 4 … 10};
- Gdy dł(s) jest równa wprowadzonej liczbie n, funkcja drukuje wprowadzony napis i kończy działanie
- W innym wypadku uruchamia pętle iterującą k razy: funkcja wywołuje samą siebie, z napisem s, do którego dodany zostanie numer iteracji, z niezmienionymi wartościami n i k.
Schemat blokowy tego algorytmu wygląda tak:
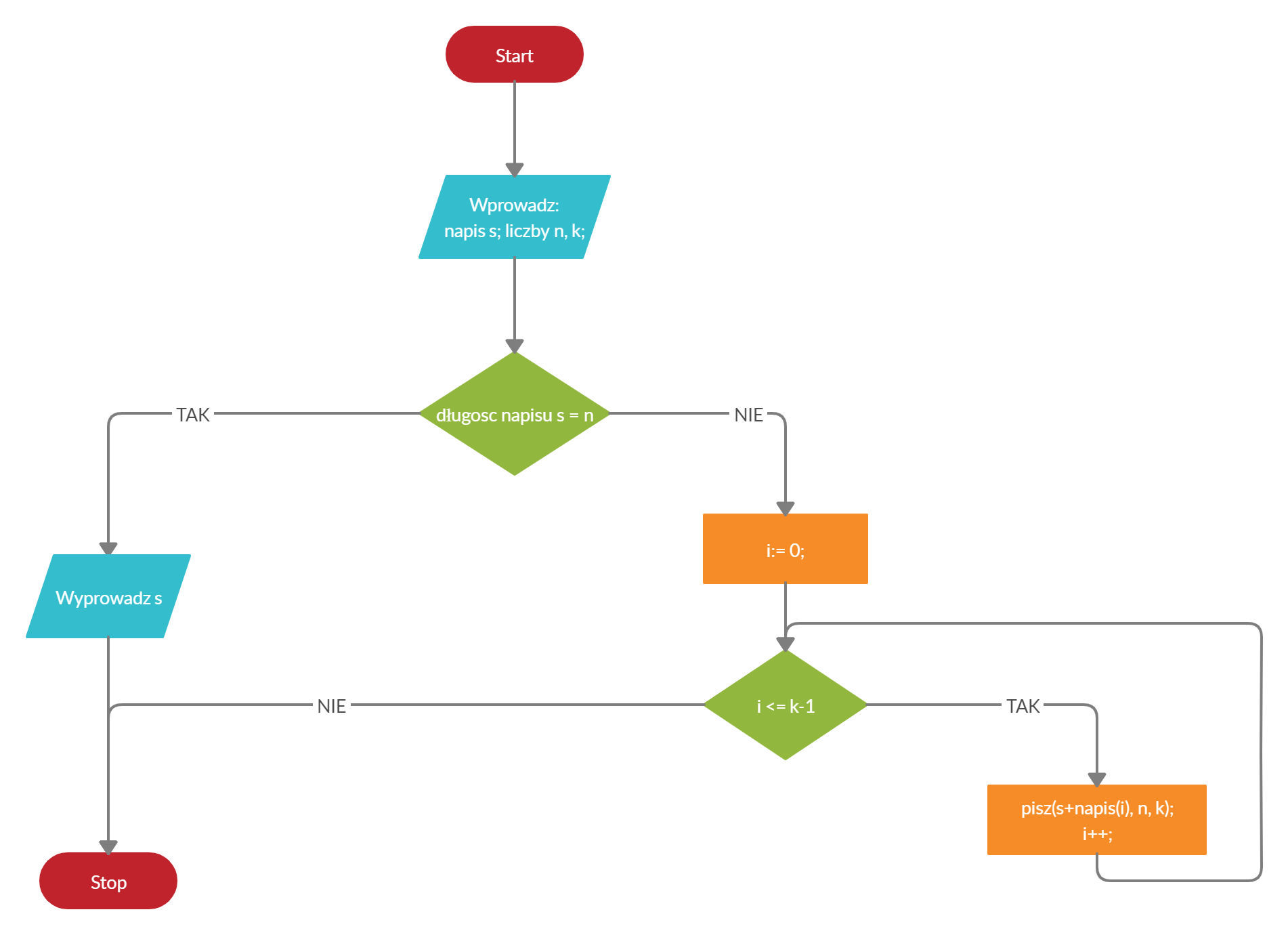
Oczywiście w schemacie tym zakładamy, że wprowadzane dane są zgodne z założeniami z zadania, a wywołanie funkcji pisz() w najniższym bloku operacyjnym jest auto-odwołaniem do naszego algorytmu. Po dokładnej analizie zarówno kolejnych kroków, jak i schematu algorytmu łatwo zauważyć, że mamy do czynienia z rekurencją (czym jest rekurencja?).
Zadanie 2 — podpunkt 1
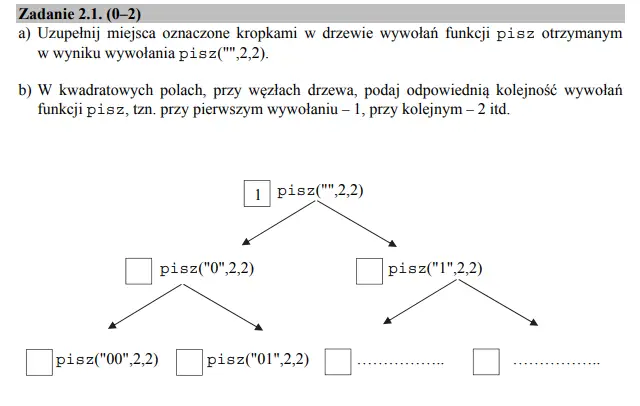
Aby wykonać ten podpunkt musimy prześledzić krok po kroku jego działanie. Znacznym ułatwieniem jest fakt, że większość drzewa jest już uzupełniona, dzięki czemu łatwiej wywnioskować kolejne wywołania. Jako iż k jest równe 2, to do napisu dodawane będzie 0 i 1, aż nie będzie miał on dwóch znaków. Z kolei kolejność wywołań zdawać by się mogło, że wystarczy ponumerować po kolei od 2 do 7. Otóż nie. Jeżeli dokładniej przyjrzymy się algorytmowi, to można zauważyć, że w pętli wywoływane są kolejne pętle, aż do osiągnięcia odpowiedniej długości napisu, dlatego należy ponumerować wywołania dla każdej gałęzi. Prawidłowe rozwiązanie całego podpunktu jest widoczne na rysunku poniżej:
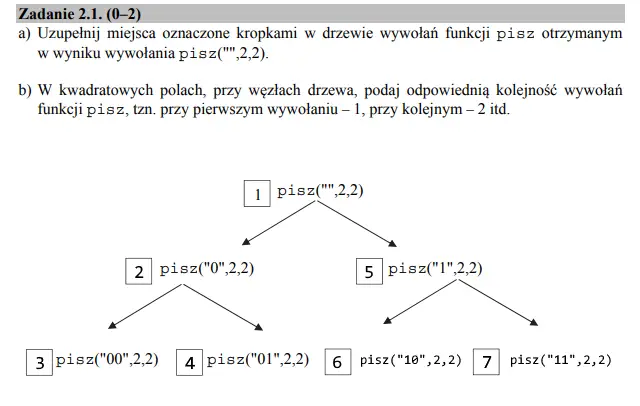
Zadanie 2 — podpunkt 2

Podpunkt ten możemy rozwiązać na dwa sposoby. Można prześledzić działanie algorytmu dla wskazanych danych wejściowych, wypisać drukowane wartości, a następnie zliczyć ilość wywołań. Rozwiązanie poprawne, ale łatwo popełnić błąd przy obliczeniach, dlatego warto podejść do zadania nieco bardziej „logicznie”. Analizując działanie algorytmu i kilka jego wyników z poprzedniego podpunktu (dla wejściowego napisu s = ”), można zauważyć, że ma on na celu wydrukować wszystkie możliwe kombinacje liczb n-cyfrowych, ze zbioru {0 … k-1}. Śledząc działania algorytmu łatwo też wyliczyć ilość jego wywołań: dla s =”, funkcja ta wywoła się 1 + k + k^2 + … + k^n razy. Dysponując powyższymi informacjami możemy uzupełnić tabelę tak jak na poniższym zdjęciu:
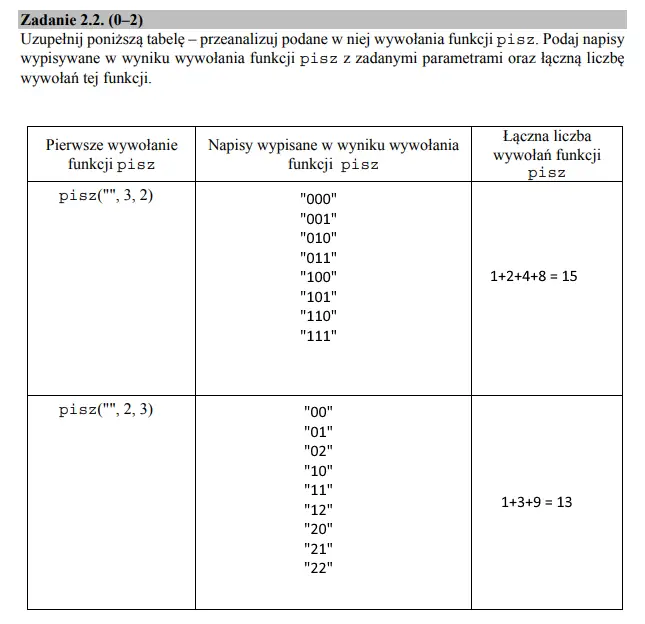
Zadanie 2 — podpunkt 3

Do tego wzoru udało nam się już dojść wyżej: 1 + k + k^2 + … + k^n. Zwracam uwagę, iż w kluczu odpowiedzi możemy znaleźć inne, równie poprawne odpowiedzi jak: (k^(n+1) — 1)/(k — 1) i (1 — k^(n+1))/(1- k). Wygodniej i łatwiej jest chyba jednak zapisanie tego tak jak podaliśmy wcześniej — jako ciąg.
Matura z informatyki 2019 odpowiedzi: zadanie 3 — prawda/fałsz

W tym zadaniu musimy wykazać się przede wszystkim wiedzą teoretyczną. Nie można przy tym popełnić błędu — jedna skucha i tracimy cały podpunkt. Poniżej znajdziesz treść podpunktów wraz z prawidłowymi odpowiedziami:
Zadanie 3 — podpunkt 1
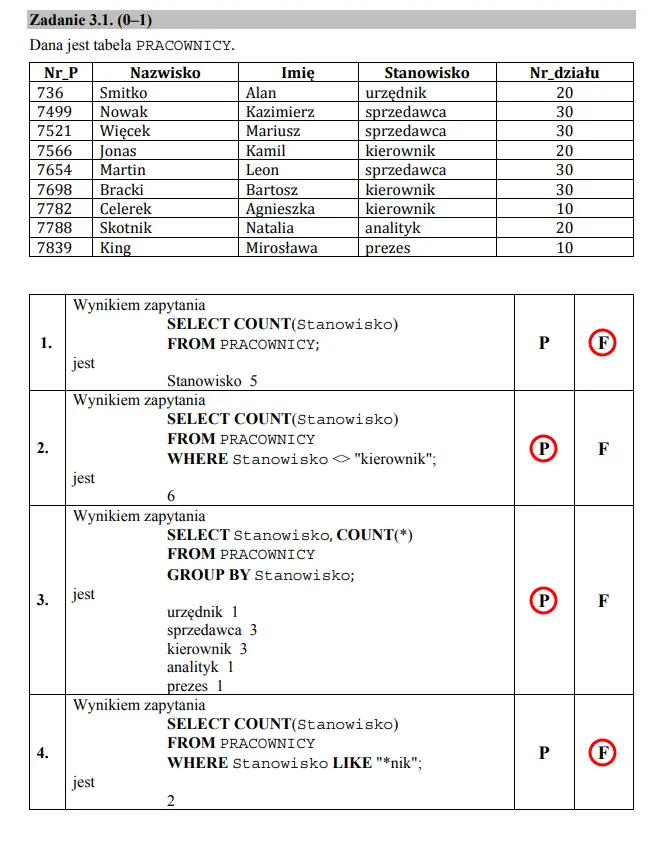
Nie jest to trudny podpunkt — w każdym przypadku operujemy na tej samej kolumnie, nie zwracając uwagi na pozostałe dane. Trzeba jednak uważać na podchwytliwość tego zadania: samo COUNT zlicza wszystkie wartości z kolumny, dopiero dodanie DISTINCT przed nazwą kolumny zliczałoby ilość unikalnych wartości.
Zadanie 3 — podpunkt 2

Dosyć proste zadanie wymagające po 1. umiejętność mnożenia (choć nikt nie broni najpierw zamienić obie liczby na liczby dziesiętne, a następnie normalne wymnożenie), a po 2. konwersji liczb z różnych systemów. Proponuje więc zapisać wynik mnożenia i wszystkich podanych liczb w bardziej „ludzkim”, dziesiętnym systemie, a następnie porównać ich wartości:

Zadanie 3 — podpunkt 3

- Skrót DNS powinien być każdemu znany — łatwo też go wywnioskować z tłumaczenia z angielskiego.
- Dobrym przykładem potwierdzającym to zdanie jest strona YouTube: wpisanie w przeglądarce zarówno youtube.com, jak i youtu.be wyświetli nam tą samą stronę, mimo że są to różne nazwy (adresy WWW).
- Przy zmianie adresu IP serwera, owszem, jest wymagana również jego zmiana w konfiguracji DNS, jednakże nazwa domeny wciąż może być ta sama — nie jest potrzebna jej zmiana.
- Systemy DNS dysponują ponad trzynastoma, rozsianymi po całym świecie serwerami.

Matura z informatyki 2019 — część druga (praktyka)
Przed nami kolejna, praktyczna część egzaminu często uznawana przez maturzystów jako ta trudniejsza. Klasycznie otrzymujemy zestaw plików, które zapewne pójdą w ogień w takich programach jak Excel, Access, czy
w wybranym języku programowania. Na wykonanie zadań mamy 150 minut, więc nie zwlekając przechodzimy do ich rozwiązywania:
Matura z informatyki 2019 rozwiązania: Zadanie 4 — liczby

Z treści wynika, iż będziemy musieli odczytywać dane z pliku liczby.txt, dlatego przygotujmy bazowe kodu, które będą początkowo drukować wiersz po wierszu zawartość pliku w konsoli — modyfikując je rozwiążemy dalsze podpunkty. Poniżej kody źródłowe w Javie, Pythonie i C++:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
#include <fstream> #include <string> #include <iostream> using namespace std; int main(){ string line; // aktualny wiersz ifstream file("liczby.txt"); // inicjalizacja pliku; wymagana sciezka do pliku if(file.is_open()){ // jezeli uda się otworzyć plik while (getline (file,line)){ // dopoki są jeszcze wiersze, odczytuj je do zmiennej cout << line << endl; // a następnie drukuj w konsoli } file.close(); // zamykamy plik } return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
package matura; import java.io.BufferedReader; import java.io.File; import java.io.FileReader; import java.io.IOException; public class Main { public static void main(String[] args) throws IOException { File f = new File("liczby.txt"); //tworzymy zmienna plikowa if (!f.exists()) { //przed rozpoczeciem pracy z plikiem nalezy sprawdzic, czy w ogole istnieje System.out.println("Podany plik nie istnieje."); return; } BufferedReader br = new BufferedReader(new FileReader(f)); //tworzymy instancje BufferedReadera if (br.ready()) { //jezeli BR jest gotowy do oczytu String line; // tworzymy zmienna przechowujaca aktualny wiersz while ((line = br.readLine()) != null) { //zczytujemy kazdy wiersz System.out.println(line); //drukujemy zawartosc pliku } } br.close(); // na koniec zamykamy plik } } |
Python
|
1 2 3 4 5 |
file = open("liczby.txt", "r") #jezeli plik nie bedzie istnial, to program zwroc blad lines = file.read().splitlines() #pozbywamy sie znakow nowego wiersza file.close() #zamykamy plik for line in lines: print(line) #drukujemy zawartosc pliku |
Pamiętaj również, że możesz sprawdzić czy zmodyfikowany kod działa zgodnie z warunkami polecenia, poprzez przepuszczenie przez niego pliku przyklad.txt i porównanie wyniku z tym podanym w zadaniu.
Zadanie 4 — podpunkt 1

Aby wykonać zadanie należy sprawdzić każdą liczbę z osobna. Wiedząc, że każda liczba jest w oddzielnym wierszu, wystarczy zmodyfikować bazowy kod, aby sprawdzał warunki z zadania, a następnie zliczał ilość liczb spełniających warunki. Oto kody źródłowe takiego programu:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
#include <fstream> #include <string> #include <iostream> #include <math.h> using namespace std; int main() { string line; //aktualny wiersz ifstream file("liczby.txt"); //inicjalizacja pliku; wymagana sciezka do pliku int count = 0; // inicjalizacja licznika potęg if(file.is_open()){ //jezeli uda się otworzyć plik while (getline (file,line)){ //dopoki są jeszcze wiersze, odczytuj je do zmiennej int a = stoi(line); // aby wykonać zadanie musimy przekonwertować tekst na liczbę float l = log(a)/log(3); // liczymy logarytm o podstawie 3 z podanej liczby(wykorzystalismy wzor na zamiane podstaw logarytmu) if(l == (int)l){ //jezeli logarytm ten jest liczbą całkowitą (co oznaczałoby, ze iterowana liczba jest potęgą trojki) count++; //zwiększ licznik o 1 } } file.close(); // zamykamy plik } cout <<"Ilosc poteg liczby 3 w pliku liczby.txt: " << count << endl; //drukuj rozwiązanie return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
package matura; import java.io.BufferedReader; import java.io.File; import java.io.FileReader; import java.io.IOException; public class Main { public static void main(String[] args) throws IOException { File f = new File("liczby.txt"); //tworzymy zmienna plikowa if (!f.exists()) { //przed rozpoczeciem pracy z plikiem nalezy sprawdzic, czy w ogole istnieje System.out.println("Podany plik nie istnieje."); return; } BufferedReader br = new BufferedReader(new FileReader(f)); //tworzymy instancje BufferedReadera if (br.ready()) { //jezeli BR jest gotowy do oczytu String line; // tworzymy zmienna przechowujaca aktualny wiersz int count = 0; while ((line = br.readLine()) != null) { //zczytujemy kazdy wiersz int a = Integer.parseInt(line); // aby wykonac zadanie musimy przekonwertowac tekst na liczbe float l = (float)(Math.log(a) / Math.log(3)); // liczymy logarytm o podstawie 3 z podanej liczby(wykorzystalismy wzor na zamiane podstaw logarytmu) if (l == (int) l) { //jezeli logarytm ten jest liczba calkowita (co oznaczaloby, ze iterowana liczba jest potega trojki) count++; //zwieksz licznik o 1 } } System.out.println("Ilosc poteg liczby 3 w pliku liczby.txt:" + count); } br.close(); // na koniec zamykamy plik } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import math file = open("liczby.txt", "r") #jezeli plik nie bedzie istnial, to program zwroc blad lines = file.read().splitlines() #pozbywamy sie znakow nowego wiersza count = 0 #inicjalizacja licznika potęg for line in lines: #iterujemy poprzez zawartosc pliku a = int(line) #konwertujemy tekst na liczbe log = round(math.log(a, 3), 6) #liczymy logarytm o podstawie 3 z podanej liczby if log.is_integer(): #jezeli logarytm z n jest liczba calkowita, to oznacza, ze n jest potega trojki count += 1 #zwiekszamy wiec licznik o 1 print("Ilosc poteg liczby 3: " + str(count)) file.close() #zamykamy plik |
Odpowiedzią jest 18 liczb. Zwracam uwagę, że niektóre kompilatory mogą mieć problem z odnalezieniem funkcji stoi() w języku C++(zamieniającej tekst na liczbę). W takim wypadku należy znaleźć opcje kompilatora i dodać -std=c++11 do wiersza poleceń konsolidatora. Dodatkowo należy pamiętać o dodaniu dodatkowej dyrektywy math.h w C++ i imporcie math w Pythonie, aby możliwe było policzenie logarytmu. W Javie zaś użyłem statycznej funkcji z klasy Math.
Zadanie 4 — podpunkt 2

Kolejne polecenie, w którym wymagana jest iteracja przez cały plik. Dodatkowo będziemy musieli rozbić liczby na tablice znaków, a następnie porównywać sumę silni z całą liczbą. Wykorzystamy tu fakt, że w C++ i Javie każdy char może być reprezentowany jako int, przy odjęciu od niego chara ’0′. W Pythonie zaś wystarczy wykonać rzutowanie do liczby całkowitej. Stworzymy również funkcje rekurencyjne liczące silnię (oczywiście, przy zastosowaniu odpowiednich warunków, możliwa jest jej implementacja przy użyciu funkcji iteracyjnej).
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
#include <fstream> #include <string> #include <iostream> #include <vector> using namespace std; int silnia(int n) { if(n==0){ //Warunek STOP return 1; } return silnia(n-1)*n; } int main() { string line; //aktualny wiersz vector<int> liczby; //zmienna przechowujaca liczby spelniajace warunki ifstream file("liczby.txt"); //inicjalizacja pliku; wymagana sciezka do pliku if(file.is_open()){ //jezeli uda sie otworzyc plik while (getline (file,line)){ //dopoki sa jeszcze wiersze, odczytuj je do zmiennej int a = stoi(line); // aby wykonac zadanie musimy przekonwertowac tekst na liczbe; przyda nam sie ona przy porownywaniu const char* cyfry = line.c_str(); //zamieniamy wiersz na tablice znakow int suma = 0; //suma silni for(int i = 0; i < line.length();i++){ //iterujemy poprzez zapisane cyfry int n = cyfry[i] - '0'; // konwersja char na int suma += silnia(n); //dodajemy silnie z liczby calkowitej do finalnej sumy } if(suma == a){ //jezeli finalna suma jest rowna tej liczbie liczby.push_back(a); //dodaj ja do listy } } file.close(); // zamykamy plik } for(auto i : liczby){ // iteracja typu foreach przez zapisane liczby cout << i << endl; //drukuj rozwiazanie } return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
package matura; import java.io.BufferedReader; import java.io.File; import java.io.FileReader; import java.io.IOException; public class Main { public static int silnia(int n) { //tworzymy rekurencyjna funkcje liczaca silnie z n if (n == 0) return 1; return silnia(n - 1) * n; } public static void main(String[] args) throws IOException { File f = new File("liczby.txt"); //tworzymy zmienna plikowa if (!f.exists()) { //przed rozpoczeciem pracy z plikiem nalezy sprawdzic, czy w ogole istnieje System.out.println("Podany plik nie istnieje."); return; } BufferedReader br = new BufferedReader(new FileReader(f)); //tworzymy instancje BufferedReadera if (br.ready()) { //jezeli BR jest gotowy do oczytu String line; // tworzymy zmienna przechowujaca aktualny wiersz while ((line = br.readLine()) != null) { //zczytujemy kazdy wiersz int a = Integer.parseInt(line); //zamieniamy wiersz na liczbe int suma = 0; //suma silnii for (char c: line.toCharArray()) { //iterujemy przez znaki w wierszu int n = c - '0'; //zamieniamy znak na liczbe calkowita suma += silnia(n); // a nastepnei dodajemy do sumy silnie z niej } if (suma == a) { //jezeli suma silnii jest rowna liczbie System.out.println(a); //wypisujemy ja } } } br.close(); // na koniec zamykamy plik } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
def silnia(n): #definiujemy rekurencyjna funkcje liczaca silnie if n == 0: #warunek stop return 1 return silnia(n-1)*n file = open("liczby.txt", "r") #jezeli plik nie bedzie istnial, to program zwroc blad File = file.read().splitlines() #pozbywamy sie znakow nowego wiersza file.close() #zamykamy plik for line in File: #iterujemy poprzez zawartosc pliku if len(line) == 0: #jezeli wiersz jest pusty, to go pomin continue liczba = int(line) #zamieniamy tekst na liczbe suma = 0 # tworzymy zmienna przechowujaca sume silnii for char in line: #nastepnie iterujemy poprzez kazda cyfre w liczbie n = int(char) #zamieniamy ja z char na int suma += silnia(n) #a nastepnie dodajemy do sumy jej silnie if suma == liczba: #jezeli suma silnii cyfr liczby jest jest jej rowna print(liczba) #wypisujemy ja |
Odpowiedzią są kolejno liczby: 2; 145; 1; 40585. Możliwe jest również rozbicie liczby z wiersza poprzez iteracyjne sprawdzanie wartości reszt z dzielenia (modulo) przez 10:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
#include <fstream> #include <string> #include <iostream> #include <vector> using namespace std; int silnia(int n) { if(n==0){ //Warunek STOP return 1; } return silnia(n-1)*n; } bool sprawdzWarunek(string line) { //tworzymy funkcje sprawdzajaca, czy dana liczba spelnia warunek z zadania int n = stoi(line); // przechowujemy liczbe w zmiennej int sum = 0; //suma silni while(n > 0){ // dopoki przechowana liczba jest wieksza od 0 sum += silnia(n % 10); // dodawaj silnie z reszty dzielenia przez 10 (reszta z dzielenia przez 10 da nam zawsze ostatnia cyfre z liczby) n /= 10; // pomniejsz przechowana liczbe o jedna cyfre } return sum == stoi(line); // zwroc, czy liczby sa takie same } int main() { string line; //aktualny wiersz vector<int> liczby; //zmienna przechowujaca liczby spelniajace warunki ifstream file("liczby.txt"); //inicjalizacja pliku; wymagana sciezka do pliku if(file.is_open()){ //jezeli uda sie otworzyc plik while (getline (file,line)){ //dopoki sa jeszcze wiersze, odczytuj je do zmiennej if(sprawdzWarunek(line)){ //jezeli finalna suma jest rowna tej liczbie liczby.push_back(stoi(line)); //dodaj ja do listy } } file.close(); // zamykamy plik } for(auto i : liczby){ // iteracja typu foreach przez zapisane liczby cout << i << endl; //drukuj rozwiazanie } return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
package matura; import java.io.BufferedReader; import java.io.File; import java.io.FileReader; import java.io.IOException; public class Main { public static int silnia(int n) { //tworzymy rekurencyjna funkcje liczaca silnie z n if (n == 0) return 1; return silnia(n - 1) * n; } static boolean sprawdzWarunek(String line) { //tworzymy funkcje sprawdzajaca, czy dana liczba spelnia warunek z zadania int n = Integer.parseInt(line); // przechowujemy liczbe w zmiennej int sum = 0; //suma silni while (n > 0) { // dopoki przechowana liczba jest wieksza od 0 sum += silnia(n % 10); // dodawaj silnie z reszty dzielenia przez 10 (reszta z dzielenia przez 10 da nam zawsze ostatnia cyfre z liczby) n /= 10; // pomniejsz przechowana liczbe o jedna cyfre } return sum == Integer.parseInt(line); // zwroc, czy liczby sa takie same } public static void main(String[] args) throws IOException { File f = new File("liczby.txt"); //tworzymy zmienna plikowa if (!f.exists()) { //przed rozpoczeciem pracy z plikiem nalezy sprawdzic, czy w ogole istnieje System.out.println("Podany plik nie istnieje."); return; } BufferedReader br = new BufferedReader(new FileReader(f)); //tworzymy instancje BufferedReadera if (br.ready()) { //jezeli BR jest gotowy do oczytu String line; // tworzymy zmienna przechowujaca aktualny wiersz while ((line = br.readLine()) != null) { //zczytujemy kazdy wiersz if (sprawdzWarunek(line)) { //jezeli suma silnii jest rowna liczbie System.out.println(line); //wypisujemy ja } } } br.close(); // na koniec zamykamy plik } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
def silnia(n): #definiujemy rekurencyjna funkcje liczaca silnie n = int(n) if n == 0: #warunek stop return 1 return silnia(n-1)*n def sprawdzWarunek(s): #definujemy funkcje sprawdzajaca warunek zadania n = int(s) #zamieniamy tekst na liczbe sum = 0 #tworzymy zmienna przechowujaca sume silnii while n > 0: #dopoki n jest wieksze od 0 sum += silnia(n % 10) #liczmy silnie z reszty z dzielnia n/10 - ostatniej cyfry n n /= 10 #zmniejszamy n dziesieciokrotnie n = int(n) #zamieniamy n na liczbe calkowita return sum == int(s) #zwaracamy czy obie liczby sa rowne file = open("liczby.txt", "r") #jezeli plik nie bedzie istnial, to program zwroc blad lines = file.read().splitlines() #pozbywamy sie znakow nowego wiersza file.close() #zamykamy plik for line in lines: #iterujemy poprzez zawartosc pliku if sprawdzWarunek(line): #jezeli spelnia warunek zadania print(line) #drukuj liczbe |
Istotnie, powyższy sposób wygląda znacznie przejrzyściej niż konwersja symboli na liczby całkowite. Pamiętajcie jednak o dodaniu dyrektywy vector – potrzebna nam ona jest do przechowywania prawidłowych liczb.
Zadanie 4 — podpunkt 3


Dosyć skomplikowane zadanie, w którym proponuje załadowanie liczb do oddzielnej tablicy, a następnie iteracje poprzez nią. Wykorzystamy podpowiedź Uwaga z treści zadania. Musimy jednak wziąć też pod uwagę możliwość, że ciągi mogą się pokrywać (pewien wyraz może być jednocześnie ostatnim wyrazem jednego ciągu, ale też i pierwszym wyrazem następnego ciągu). Do obliczenia największego wspólnego dzielnika wykorzystamy algorytm Euklidesa. Podczas pisania kodu należy więc wziąć pod uwagę powyższe spostrzeżenia:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
#include <fstream> #include <string> #include <iostream> #include <vector> using namespace std; int NWD(int a, int b) { // funkcja znajdujaca najwiekszy wspolny dzielnik (NWD) dwoch liczb int k; // oraz definiujemy zmienna pomocnicza przy zamianie wartosci while (b != 0){ // wykorzystujemy tutaj algorytm Euklidesa k = b; b = a%b; a = k; } return a; //zwracamy najwiekszy wspolny dzielnik } int main() { vector<int> liczby; //zmienna przechowujaca liczby spelniajace warunki vector<int> finalneLiczby; //zmienna przechowujaca liczby spelniajace warunki int all[500]; // zmienne przechowujace zawartosc pliku string line; //aktualny wiersz ifstream file("liczby.txt"); //inicjalizacja pliku; wymagana sciezka do pliku int count = 0; // inicjalizacja zmiennej pomocniczej if(file.is_open()){ //jezeli uda sie otworzyc plik while (getline (file,line)){ //dopoki sa jeszcze wiersze, odczytuj je all[count] = stoi(line); // i dodawaj do tablicy count++; } } file.close(); // zamykamy plik int n = all[0]; // zmienna przechowujaca ostatnia liczbe lub ostatni dzielnik (zgodnie z podpowiedzia w zadaniu) int dzielnik; // finalny dzielnik, ktory zwrocimy na koncu for(int i = 1; i <500; i++){ //petla iterujaca przez zapisane liczby int nwd = NWD(n, all[i]); //liczymy Najwiekszy Wspolny Dzielnik dla przechowanej liczby/dzielnika if(nwd != 1){ // jezeli maja wspolny dzielnik (inny niz 1) if(liczby.empty()){ //sprawdzamy najpierw czy pomocniczy zbior liczb jest pusty (co oznaczaloby, ze w n jest przechowana liczba, a nie dzielnik) liczby.push_back(n); // jezeli tak to od razu dodajemy ta liczbe do zbioru (aby jej nie pominac) } liczby.push_back(all[i]); // nastepnie dodajemy liczbe z aktualnego wiersza n = nwd; // i przypisujemy za n nowy dzielnik } else { //w przeciwnym wypadku if(liczby.size() > finalneLiczby.size()){ //sprawdzamy czy pomocniczy zbior jest dluzszy, niz ten finalny finalneLiczby = liczby; // jezeli tak to zapisujemy go jako finalny dzielnik = n; // i zapisujemy finalny dzielnik } if(!liczby.empty()){ // jezeli zas pomocniczy zbior nie jest pusty (co oznacza, ze wlasnie znalezlismy koniec ciagu) if(NWD(liczby[liczby.size()-1], all[i]) > 1){ //musimy sprawdzic, czy ostatnia liczba ze zbioru pomocniczego nie posiada wspolnych dzielnikow z aktualnie sprawdzana liczba (musimy to zrobic, dlatego ze za n przypisany jest dzielnik, a nie liczba) int a = liczby[liczby.size()-1]; // jezeli liczby maja wspolny dzielnik liczby.clear(); // czyscimy zbior pomocniczy liczby.push_back(a); // a nastepnie dodajemy do niego od razu dwie liczby liczby.push_back(all[i]); // ktore spelniaja warunki zadania } else{ liczby.clear(); // w innym razie po prostu czyscimy zbior pomocniczy } } n = all[i]; // na koniec za n przypisujemy aktualna liczbe (aby na poczatku petli mozna bylo policzyc nowy NWD) } } cout << "Pierwsza liczba z ciagu: " << finalneLiczby[0] << ", dzielnik: " << dzielnik << ", dlugosc ciagu: " << finalneLiczby.size(); return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
package matura; import java.io.BufferedReader; import java.io.File; import java.io.FileReader; import java.io.IOException; import java.util.ArrayList; public class Main { public static int NWD(int a, int b) { //tworzymy funkcje liczaca NWD dla dwoch liczb int k; while (b != 0) { //wykorzystujemy tutaj algorytm Euklidesa k = b; b = a % b; a = k; } return a; } public static void main(String[] args) throws IOException { File f = new File("liczby.txt"); //tworzymy zmienna plikowa if (!f.exists()) { //przed rozpoczeciem pracy z plikiem nalezy sprawdzic, czy w ogole istnieje System.out.println("Podany plik nie istnieje."); return; } BufferedReader br = new BufferedReader(new FileReader(f)); //tworzymy instancje BufferedReadera if (br.ready()) { //jezeli BR jest gotowy do oczytu String line; // tworzymy zmienna przechowujaca aktualny wiersz ArrayList < Integer > ciag = new ArrayList < Integer > (); //zmienna przechowujaca liczby spelniajace warunki int dzielnik; //zmienna przechowujaca aktualny dzielnik (lub pierwsza liczbe ciagu) int pierwszaMax = 0; //zmienna przechowujaca pierwsza liczbe ciagu int dlugoscMax = 0; //zmienna przechowujaca dlugosc ciagu int dzielnikMax = 1; //zmienna przchowujaca dzielnik ciagu int iterator = 0; //iterator potrzebny do wypelnienia ponizszej tablicy int[] liczby = new int[500]; //tablica liczb z zadania while ((line = br.readLine()) != null) { //zczytujemy kazdy wiersz liczby[iterator] = Integer.parseInt(line); //i wypelniamy pusta tablice liczb iterator++; } dzielnik = liczby[0]; //pierwsza liczba z pliku bedzie pierwszym dzielnikiem for (int i = 1; i < 500; i++) { //nastepnie iterujemy poprzez pozostale liczbe w poszukiwaniu najdluzszego ciagu int num = liczby[i]; //wczytujemy iterowana liczbe int nwd = NWD(num, dzielnik); //liczymy Najwiekszy Wspolny Dzielnik dla przechowanej liczby/dzielnika if (nwd != 1) { //jezeli maja wspolny dzielnik (inny niz 1) if (ciag.isEmpty()) { //sprawdzamy najpierw czy pomocniczy zbior liczb jest pusty (co oznaczaloby, ze w n jest przechowana liczba, a nie dzielnik) ciag.add(dzielnik); //jezeli tak to od razu dodajemy ta liczbe do zbioru (aby jej nie pominac) } ciag.add(num); //nastepnie dodajemy liczbe z aktualnego wiersza dzielnik = nwd; //i przypisujemy za n nowy dzielnik } else { if (ciag.size() > dlugoscMax) { //w przeciwnym wypadku sprawdzamy czy pomocniczy zbior jest dluzszy, niz przechowana dlugosc dlugoscMax = ciag.size(); //jezeli tak to zapisujemy jego dlugosc dzielnikMax = dzielnik; //dzielnik pierwszaMax = ciag.get(0); //oraz pierwszy wyraz } if (!ciag.isEmpty()) { //jezeli zas pomocniczy zbior nie jest pusty (co oznacza, ze wlasnie znalezlismy koniec ciagu) if (NWD(liczby[i - 1], num) > 1) { //musimy sprawdzic ostatni wyraz i pierwszy nastepnego ciagu int a = liczby[i - 1]; //jezeli liczby maja wspolny dzielnik ciag.clear(); //czyscimy zbior pomocniczy ciag.add(a); //a nastepnie dodajemy do niego od razu dwie liczby ciag.add(num); //ktore spelniaja warunki zadania } else ciag.clear(); //w innym razie po prostu czyscimy zbior pomocniczy } dzielnik = num; //na koniec za dzielnik przypisujemy aktualna liczbe (aby na poczatku petli mozna bylo policzyc nowy NWD) } } System.out.print("Pierwsza liczba najdluzszego ciagu: " + pierwszaMax + ", dzielnik ciagu: " + dzielnikMax + ", dlugosc ciagu: " + dlugoscMax); } br.close(); // na koniec zamykamy plik } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
def NWD(a, b): #// funkcja znajdujaca najwiekszy wspolny dzielnik (NWD) dwóch liczb k = 1 while b != 0: k = b b = a%b a = k return a file = open("liczby.txt", "r") #jezeli plik nie bedzie istnial, to program zwroc blad lines = file.read().splitlines() #pozbywamy sie znakow nowego wiersza file.close() #zamykamy plik pom = [] #zmienna przechowujaca liczby spelniajace warunki dzielnik = int(lines[0]) #zmienna przechowujaca aktualny dzielnik (lub pierwsza liczbe ciagu) pierwszaMax = 0 #zmienna przechowujaca pierwsza liczbe ciagu dlugoscMax = 0 #zmienna przechowujaca dlugosc ciagu dzielnikMax = 1 #zmienna przchowujaca dzielnik ciagu for i in range(1, 500): #iterujemy z pominieciem pierwszej liczby(bo uzylismy ja powyzej) num = int(lines[i]) #zamieniamy tekst na liczbe nwd = NWD(dzielnik, num) #liczymy Najwiekszy Wspolny Dzielnik dla przechowanej liczby/dzielnika if nwd != 1: #jeżeli mają wspólny dzielnik (inny niż 1) if len(pom) == 0: #sprawdzamy najpierw czy pomocniczy zbior liczb jest pusty (co oznaczałoby, ze w n jest przechowana liczba, a nie dzielnik) pom.append(dzielnik) #jezeli tak to od razu dodajemy ta liczbe do zbioru (aby jej nie pominac) pom.append(num) #nastepnie dodajemy liczbe z aktualnego wiersza dzielnik = nwd #i przypisujemy za n nowy dzielnik else: if len(pom) > dlugoscMax:#w przeciwnym wypadku sprawdzamy czy pomocniczy zbior jest dluzszy, niz przechowana dlugosc dlugoscMax = len(pom) #jezeli tak to zapisujemy jego dlugosc dzielnikMax = dzielnik #dzielnik pierwszaMax = pom[0] #oraz pierwszy wyraz if len(pom) != 0: #jezeli zas pomocniczy zbior nie jest pusty (co oznacza, że wlasnie znalezlismy koniec ciagu) if NWD(pom[len(pom)-1], num) > 1: #musimy sprawdzic ostatni wyraz i pierwszy nastepnego ciagu a = pom[len(pom)-1] #jezeli liczby maja wspolny dzielnik pom.clear() #czyscimy zbior pomocniczy pom.append(a) #a nastepnie dodajemy do niego od razu dwie liczby pom.append(num) #ktore spelniaja warunki zadania else: pom.clear() #w innym razie po prostu czyscimy zbior pomocniczy dzielnik = num #na koniec za dzielnik przypisujemy aktualna liczbe (aby na poczatku petli mozna bylo policzyc nowy NWD) print("Pierwsza liczba z ciagu: " + str(pierwszaMax) + ", dzielnik " + str(dzielnikMax) + ", dlugosc ciagu: " + str(dlugoscMax)) |
Oczywiście algorytm NWD może mieć postać pętli do…while – choć jest to bardziej „zasobożerne” rozwiązanie, jest ono jak najbardziej prawidłowe. Zwracam ponownie uwagę na dyrektywę vector w języku C++(rzecz jasna można zamiast niego użyć zwyczajnych tablic, jednak vectory są znacznie łatwiejsze w użytkowaniu), oraz na ArrayList z java.util w Javie. Powyższy program drukuje odpowiedź: Pierwsza liczba z ciagu: 31968, dzielnik: 74, dlugosc ciagu: 150.
Matura z informatyki 2019 arkusz: Zadanie 5 — chmury

Przyjrzyjmy się zawartości pliku pogoda.txt: dane tworzą wiersze i kolumny pooddzielane średnikami. Do wykonania podpunktów wykorzystamy więc program Microsoft Excel. Aby rozpocząć pracę musimy więc zaimportować dane z pliku, a sposób, w jaki należy to zrobić przedstawiłem krok po kroku na poniższych zrzutach ekranu:
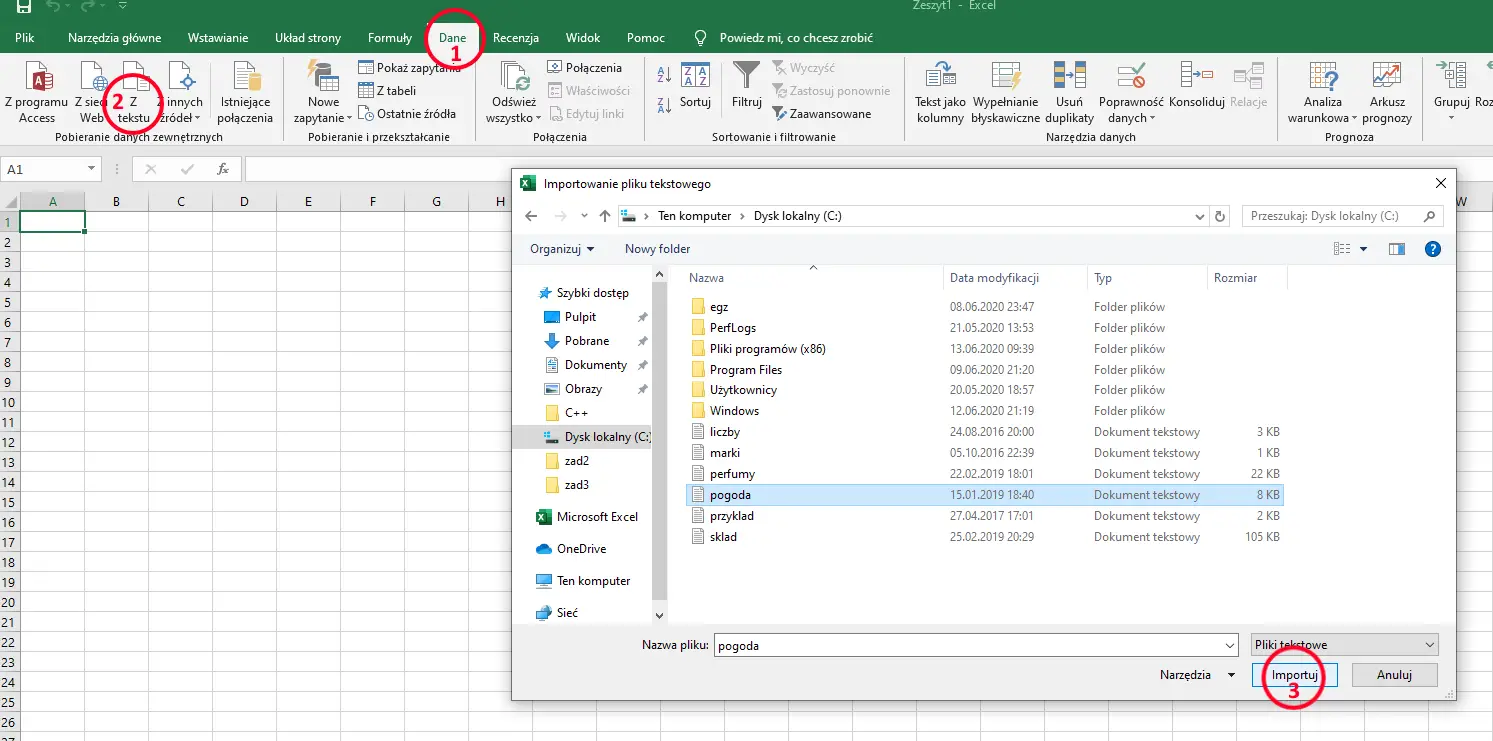
Z zakładki Dane wybieramy Z tekstu, a następnie wskazujemy plik z dysku.
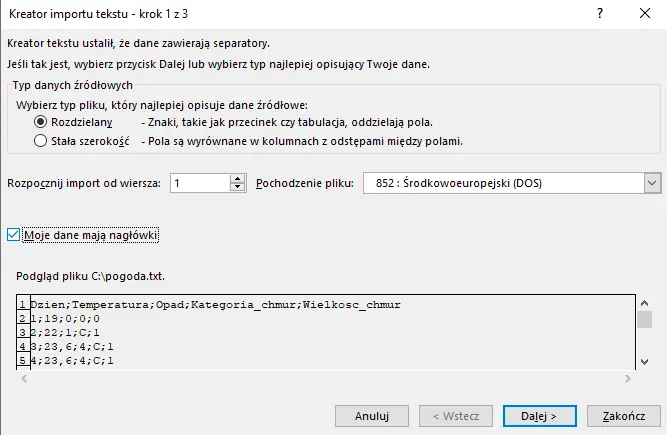
Uwaga: należy zaznaczyć Moje dane mają nagłówki.
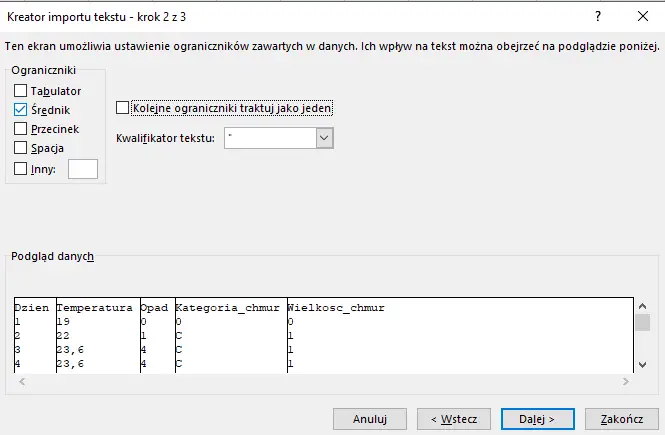
Jako ogranicznik wybieramy średnik.
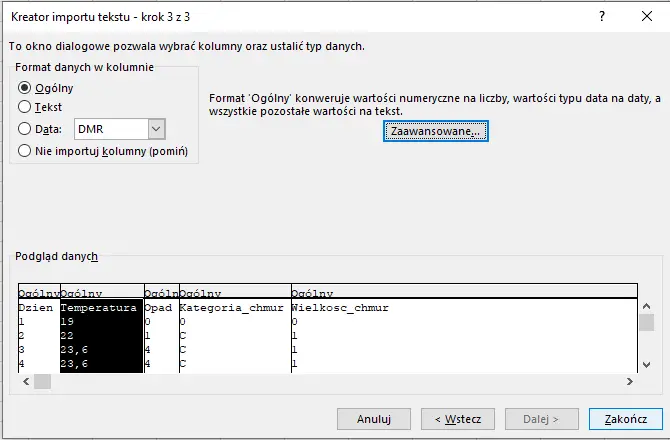
Tutaj bez zmian; klikamy Zakończ, a następnie OK.
Z tak zaimportowanym arkuszem możemy przystąpić do rozwiązywania podpunktów:
Zadanie 5 — podpunkt 1

Prosty podpunkt, w którym stworzymy nową kolumnę, w której wykorzystamy funkcje JEŻELI i ORAZ, aby zwrócić wartość 1 dla dni spełniających warunki i wartość 0 w przeciwnym wypadku. Na koniec zliczymy wszystkie wartości w nowej kolumnie za pomocą funkcji SUMA:
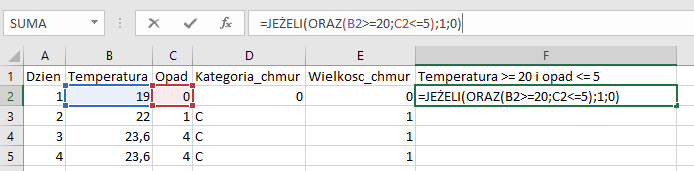
Nowa kolumna wraz z formuła warunkową;
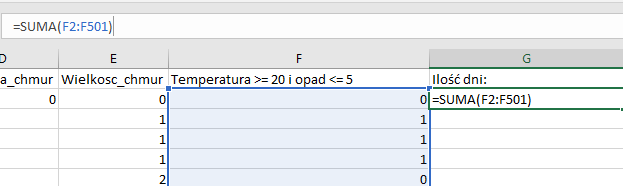
Kolumna z formułą zliczającą;

Wynik działania SUMY. Odpowiedzią jest więc 63 dni.
Zadanie 5 — podpunkt 2

Posłużymy się dwiema kolumnami: pierwsza będzie zliczać ilość dni pod rząd, w których temperatura wzrastała, zaś druga odnajdzie nam maksymalną wartość z poprzedniej kolumny, aby łatwiej było wskazać odpowiedź. Trzeba pamiętać, aby w pierwszych wierszach wpisać odpowiednie wartości „ręcznie” — formuła najprawdopodobniej się posypie gdy zostanie wpisana w pierwszej komórce:
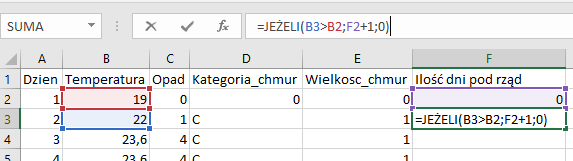
Pierwsza kolumna wraz z formułą zliczającą. Należy ją przypisać do całej kolumny poniżej poprzez podwójne kliknięcie kwadracika w prawym dolnym rogu.
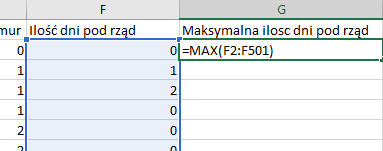
Druga, pomocnicza kolumna. Wynikiem działania tej formuły jest 8, więc należy szukać wartości 8 w kolumnie Ilość dni pod rząd – będzie to ostatni dzień z rzędu, w którym rosła temperatura.
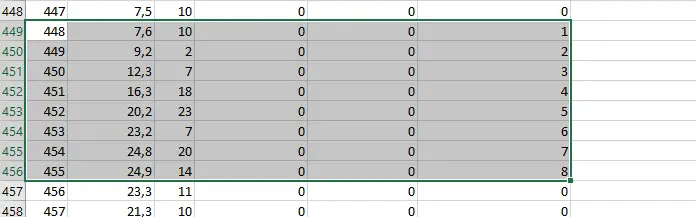
Na zrzucie widzimy zaznaczony cały okres, który spełnia warunki zadania. Trzeba uważać aby nie wziąć pod uwagę dnia 447, gdyż nie był on dniem, w którym nastąpił wzrost temperatury. Odpowiedzią jest więc okres od 448 dnia do 455 dnia.
Zadanie 5 — podpunkt 3

Nieco bardziej skomplikowany podpunkt, w którym stworzymy drugi, pomocniczy arkusz, oraz kolumnę tworzącą rodzaj chmur z ich kategorii i wielkości. Pamiętaj, że kopiując cały arkusz lub jego część, zazwyczaj przy wklejaniu należy wybrać Wklej wartości. Przy kopiowaniu sum częściowych warto skorzystać z menu F5>Specjalne… – tak jak pokazałem na poniższym obrazku:
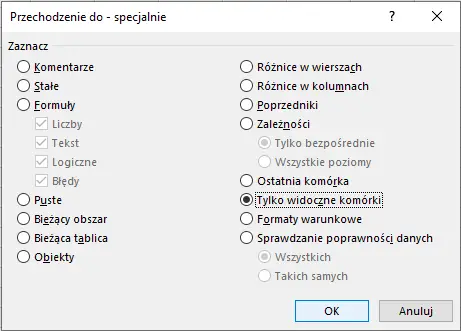
Dzięki temu unikniesz kopiowania całego „wnętrza” sumy częściowej.
Stwórzmy więc nową kolumnę Typ chmury, a w niej połączymy kolumny Kategoria i wielkość. Zaznaczam, że w sytuacji, gdy wielkość lub kategoria chmury będzie równa 0, to jej typ powinien być taki sam. Choć tych chmur (lub raczej ich braku 🙂 ) nie będziemy brać pod uwagę przy dalszych krokach, to wygląda to nieco estetyczniej:
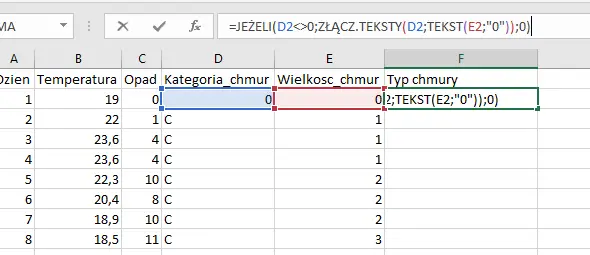
Oczywiście formułę „rozciągamy” na całą kolumnę (w poleceniu wymagają od nas zbadanie pierwszych 300 dni, jednakże nic nie stanie się, gdy kolumna będzie obejmować wszystkie dni).
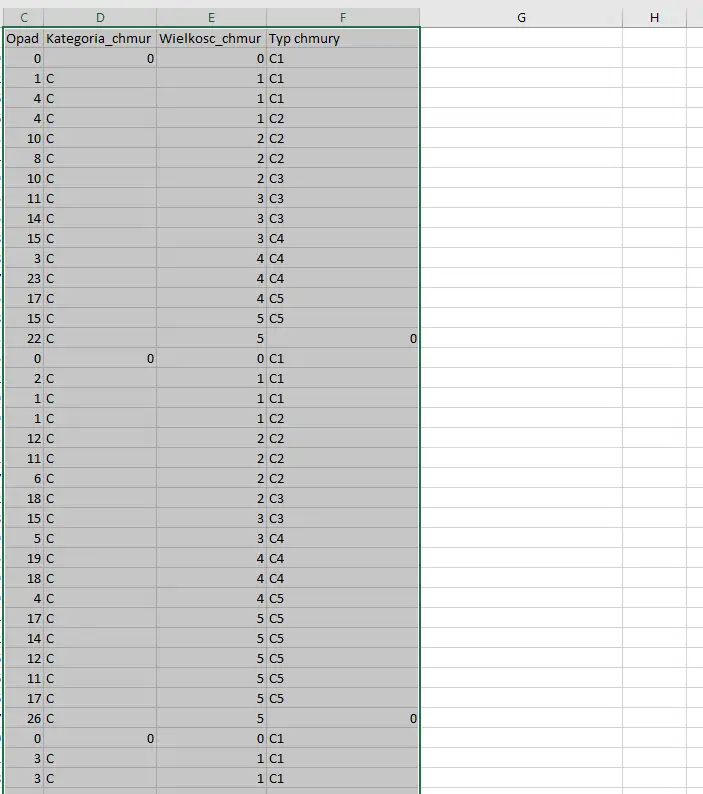
Następnym krokiem będzie skopiowanie części arkusza — najbardziej interesuje nas kolumna Opady i Typ chmury. Pamiętaj aby zaznaczyć pierwsze 300 dni.
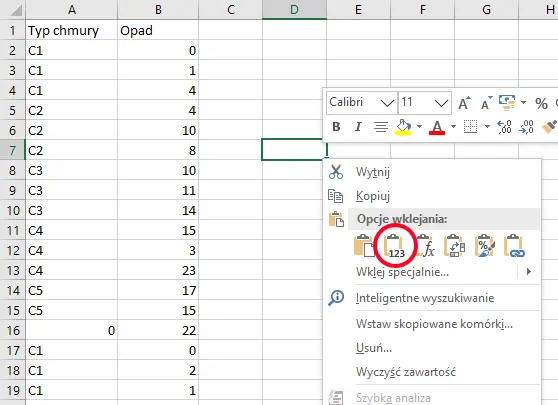
Skopiowaną część tabeli wklejamy w nowym arkuszu (sposób w jaki to zrobić pokazałem na obrazku z prawej strony). Pozbywamy się niepotrzebnych kolumn zostawiając tylko te widoczne na zrzucie.
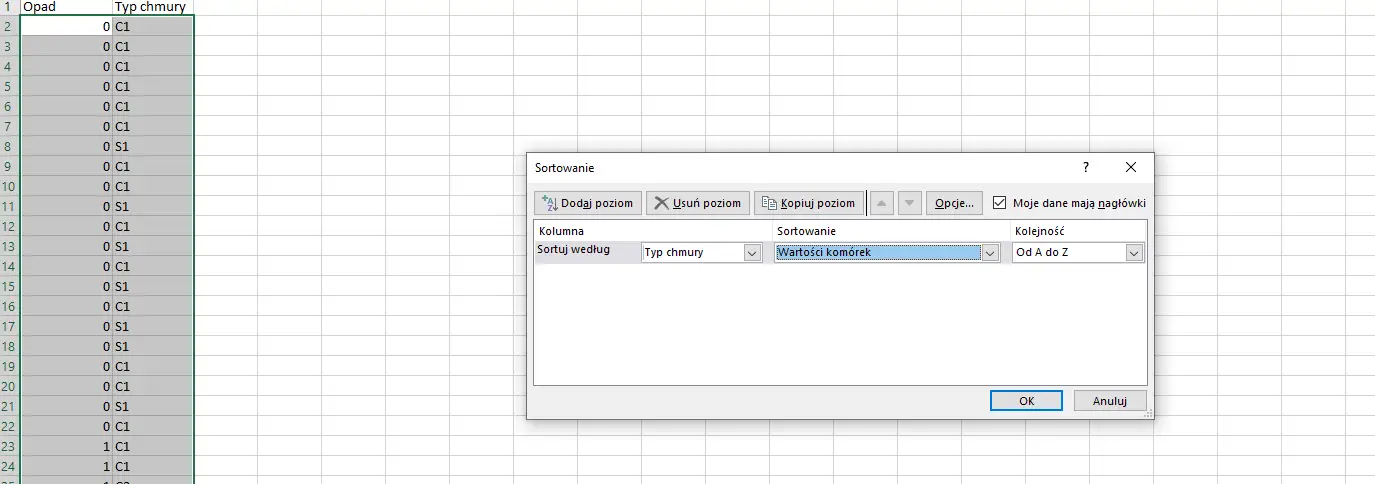
Zaznaczamy wszystkie wartości, a następnie sortujemy je (zakładka Dane>Sortuj…) tak jak na obrazku — według kolumny Typ chmury.
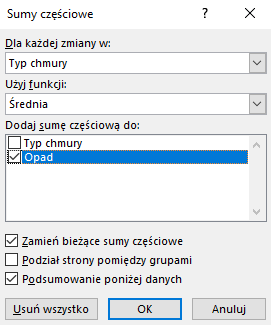
Następnie zaznaczamy całą tabelę (ctrl+a), a następnie z zakładki Dane wybieramy suma częściowa i okienko uzupełniamy tak jak ja to zrobiłem powyżej.
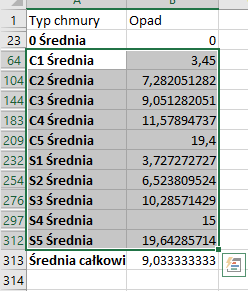
Z menu widocznego od razu po lewo wybieramy zakładkę 2, a naszym oczom ukażą się wszystkie średnie. Zaznaczmy więc interesujące nas typy chmur i skopiujmy wraz z ich średnimi opadami (przy pomocy menu Specjalnie, które pokazałem na samym początku tego podpunktu). Skopiowane dane wklejamy w innym miejscu w arkuszu.
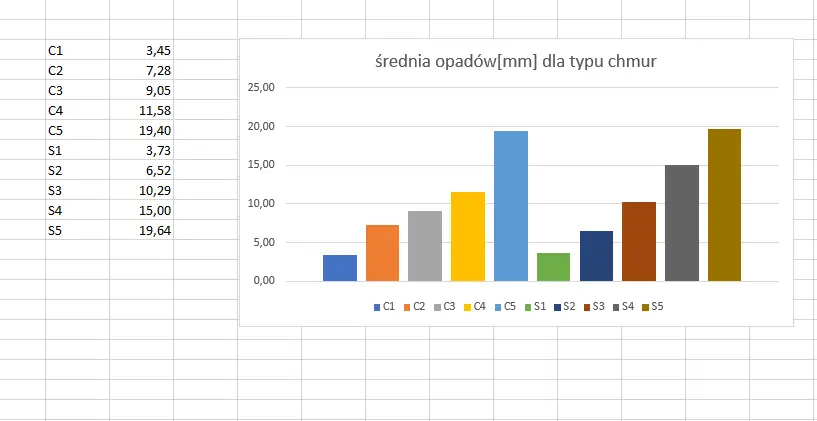
W zadaniu wymagają zaokrąglenia do drugiego miejsca po przecinku, więc zaznaczamy średnie i z zakładki Narzędzia główne, w polu liczba zamiast Ogólne wybierz Liczbowe. Następnie zaznacz nowo utworzoną tabelę i utwórz wykres z zakładki Wstawianie. Pamiętaj o czytelnym przedstawieniu danych na wykresie. Rozwiązanie widoczne jest na powyższym zdjęciu.
Zadanie 5 — podpunkt 4

Do rozwiązania tego podpunktu potrzebne nam będą dwie nowe kolumny, które przedstawią dane zgodne z teorią profesora. Ich formuły widoczne są na poniższych zdjęciach:
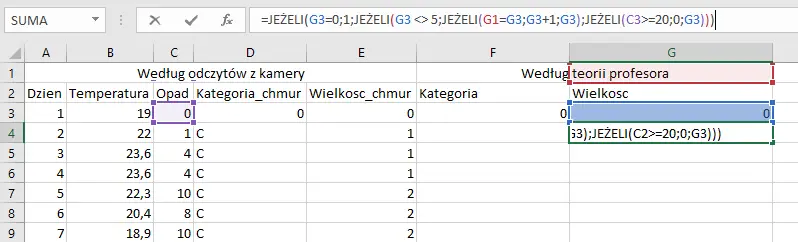
Dosyć skomplikowana formuła sprawdzająca warunki narzucone przez zadanie. Najpierw sprawdza ona, czy poprzedni dzień był bezchmurny — w takim wypadku wielkość chmury będzie zawsze równa 1. W przeciwnym razie sprawdza, czy wielkość chmury z poprzedniego dnia jest różna (mniejsza) od 5, następnie sprawdza, czy nastąpił cykl trzech dni. Jeżeli tak, to zwiększa wartość o 1, a jeżeli nie to przepisuje ich wartość. Jeżeli wielkość była równa 5 i jednocześnie opad był większy lub równy 20mm, to przyjmie ona wartość 0.
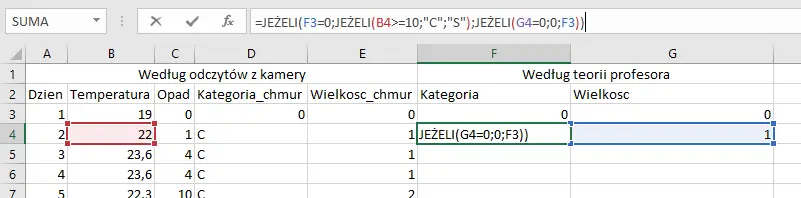
W kolejnej kolumnie należy najpierw zweryfikować, czy dzień nie jest bezchmurny, a następnie przyjąć odpowiednią wartość zależną od temperatury (o ile poprzedni dzień był bezchmurny — chmury przecież nie mogą nagle zmienić swojej kategorii).
Oczywiście podane formuły należy zastosować dla całych kolumn. Z tak przygotowanym zestawem danych możemy przystąpić do rozwiązywania pod-podpunktów:
- Proponuję skopiować nowo utworzone kolumny do nowego arkusza (pamiętaj, aby wkleić tylko wartości). Następnie z zakładki Dane>Sortuj należy posortować rosnąco według kolumny Wielkosc: Następnie zaznacz kolumnę Wielkosc i wybierz Suma częściowa z zakładki Dane. W polu Użyj funkcji wybierz Liczba, tak jak pokazałem na zrzucie:. Oto wynik działania sumy częściowej — odpowiedź do tego podpunktu (z drugiej zakładki, z lewego menu):
- Wróćmy do pierwszego arkusza, w którym dodaliśmy dwie kolumny. Aby sprawdzić, czy dane wg. teorii profesora zgadzają się z tymi faktycznymi, wystarczy wykorzystać formułę JEŻELI zwracającą 1 w przypadku, gdy będą się zgadzać i 0 w przeciwnym wypadku. Następni za pomocą formuły SUMA zliczymy ilość takich dni. Pamiętaj, aby uwzględnić pierwsze 300 dni w formułach: Ustawiamy formułę na całą kolumnę, a następnie sumujemy jej wartości dla pierwszych 300 dni: Odpowiedzią jest więc 296 dni.
- Podpunkt ten wykonujemy analogicznie do poprzedniego, porównując jednak kolumny Kategoria_chmur i Kategoria. Końcowy wynik powinien być podobny do tego na obrazku: Odpowiedzią jest 286 dni.
Matura z informatyki 2019 rozwiązania: zadanie 6 — Perfumeria

Do rozwiązania tego zadania przyda nam się program Microsoft Access. Należy więc zaimportować podany przez CKE plik, a następnie połączyć tabele relacjami. Poniżej pokazane jest jak krok po kroku to zrobić:
Z menu Dane wybieramy Nowe źródło danych tak jak na zdjęciu;
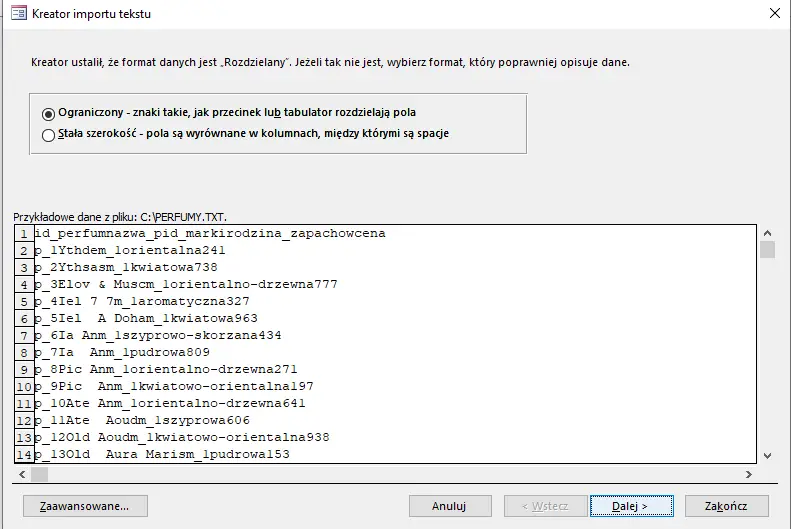
Bez zmian;
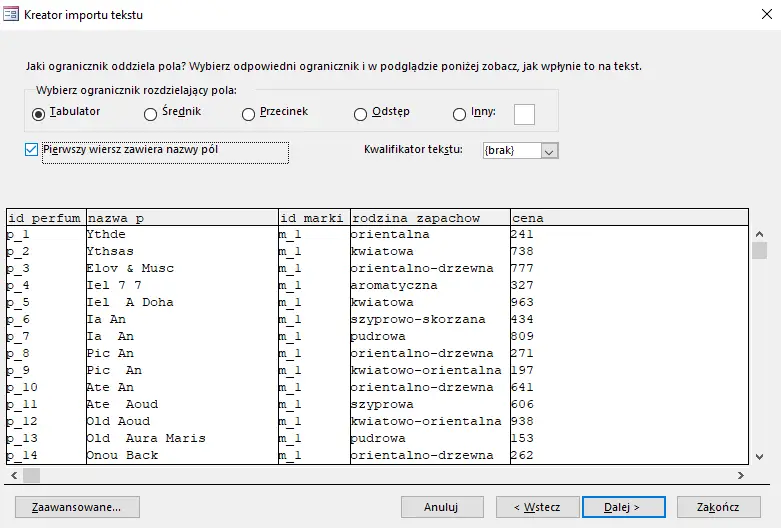
Zaznaczamy Pierwszy wiersz zawiera nazwy pól;
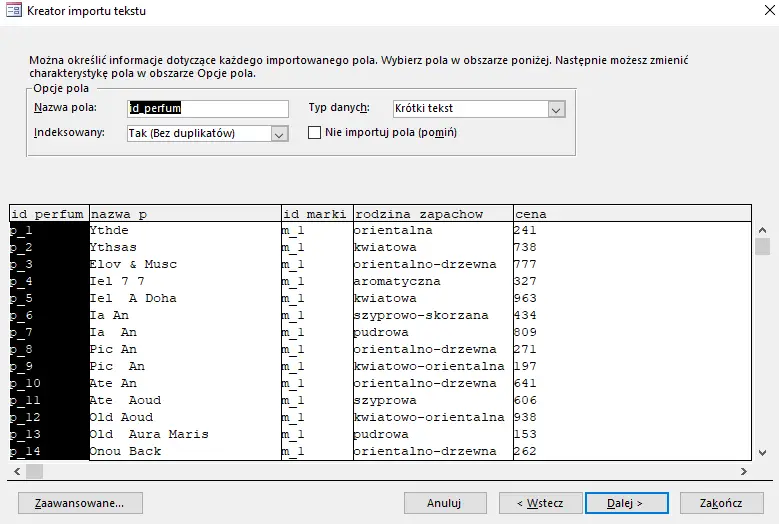
Jeżeli pole jest identyfikatorem, to nie może być duplikatów — trzeba to zaznaczyć;
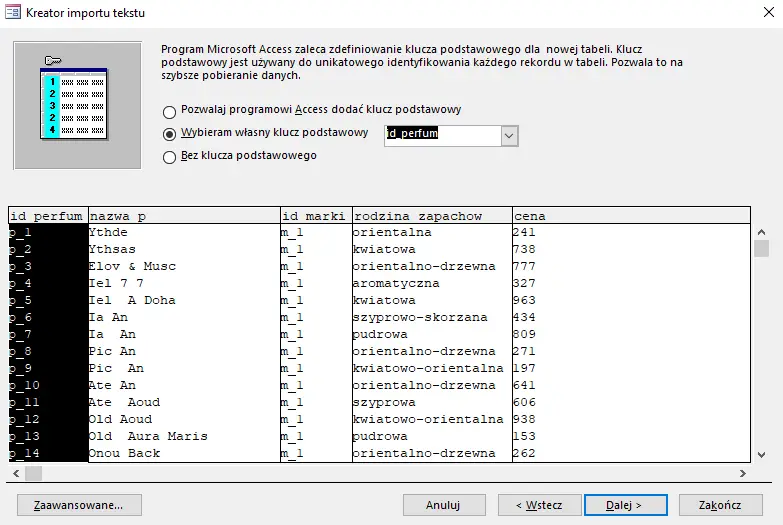
Pole z identyfikatorem będzie kluczem głównym. Można kliknąć Zakończ.
Powyższe operacje wykonujemy analogicznie dla wszystkich plików dołączonych do zadania. Uwaga: dla pliku sklad.txt, wybierz Bez klucza podstawowego i Tak (Duplikaty OK) – pole id_perfum jest w tej tabeli kluczem obcym. Następnym krokiem jest połączenie tabeli relacjami (Narzędzia bazy danych>Relacje) w sposób pokazany na zdjęciu (pamiętaj aby zaznaczyć Wymuszaj więzy integralności):
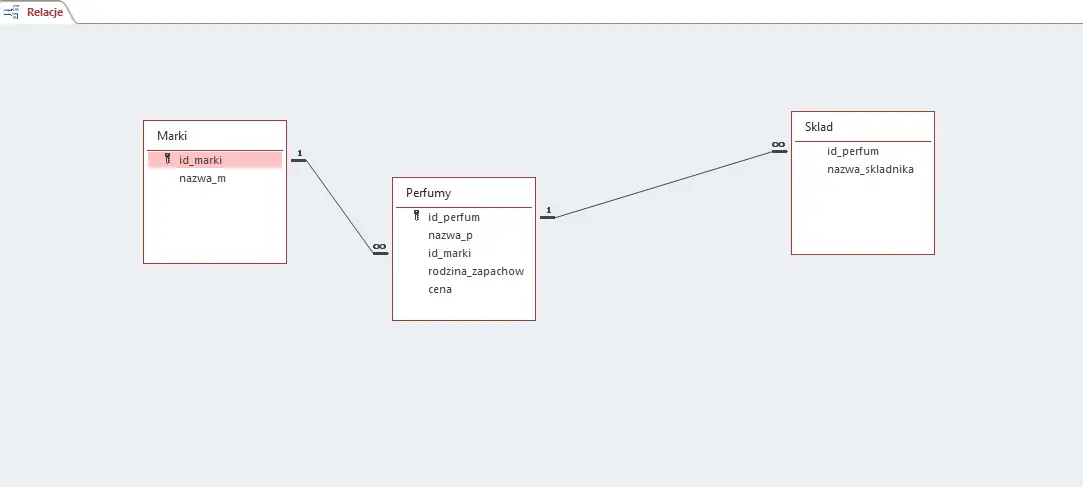
Gdy mamy już zaimportowaną bazę, możemy przejść do rozwiązywania zadania.
Zadanie 6 — podpunkt 1

Wykorzystamy tutaj prostą kwerendę odnajdującą według warunku. Stwórz więc kwerendę i uzupełnij ją tak jak na zrzucie poniżej:
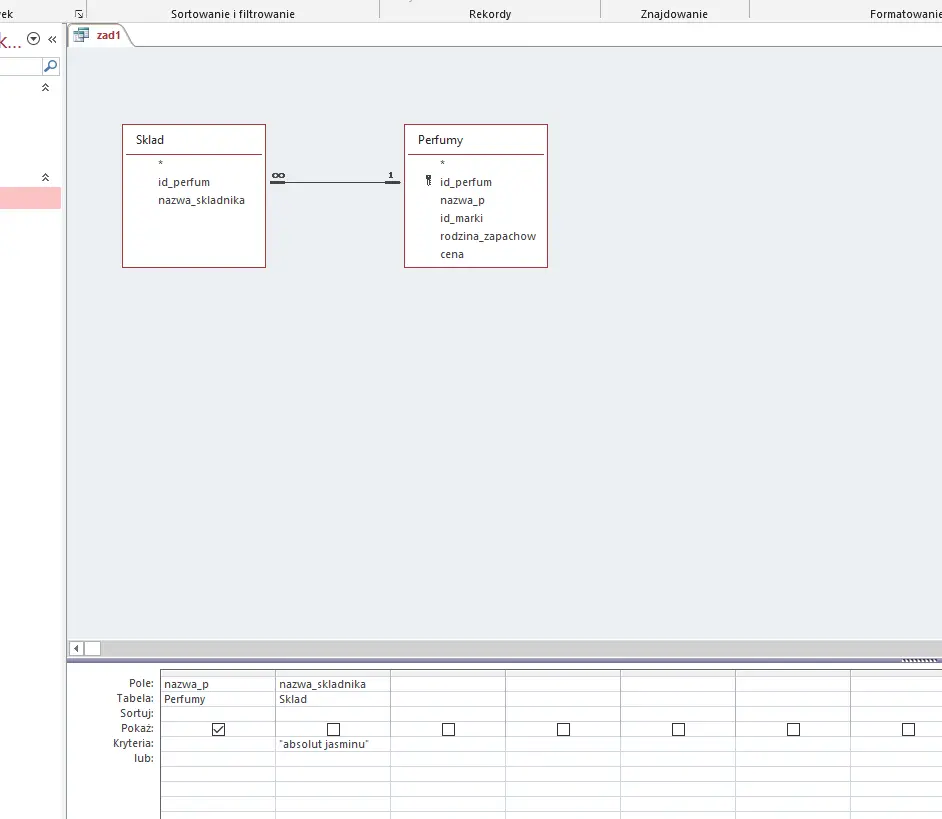
Wynik działania kwerendy i odpowiedź na zadanie widoczne są poniżej:
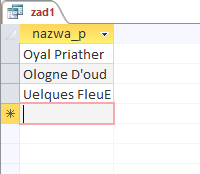
Zadanie 6 — podpunkt 2

Do wykonania tego podpunktu potrzebna nam będzie pomocnicza kwerenda, która znajdzie najniższą cenę dla każdej z rodzin. Jej zawartość widoczna jest na poniższym zdjęciu:
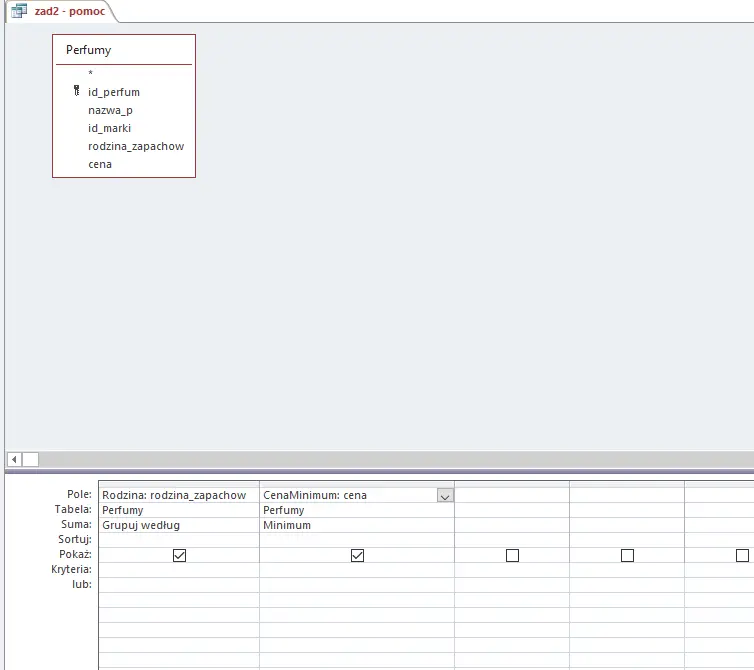
Pamiętaj, że aby pogrupować pola musisz kliknąć Sumy z zakładki Projektowanie. Dla ułatwienia dobrym pomysłem jest też nadanie własnych nazw polom (Rodzina i CenaMinimum).
Następnym krokiem jest stworzenie finalnej kwerendy, która da nam odpowiedź. Musimy w niej dodać tabelę Perfumy oraz kwerendę, którą przed chwilą stworzyliśmy:
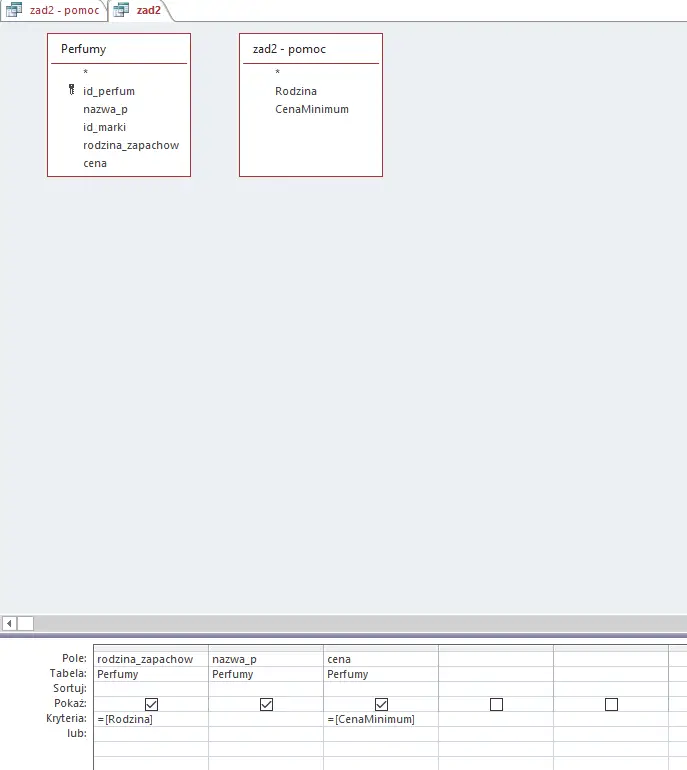
Uzupełniamy kwerendę tak jak pokazano.
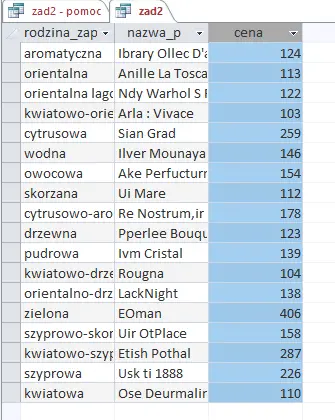
Wywołanie kwerendy daje nam odpowiedź na ten podpunkt.
Zadanie 6 — podpunkt 3

Ponownie potrzebne będzie wykorzystanie pomocniczej kwerendy. W tym podpunkcie skorzystamy również z języka SQL.
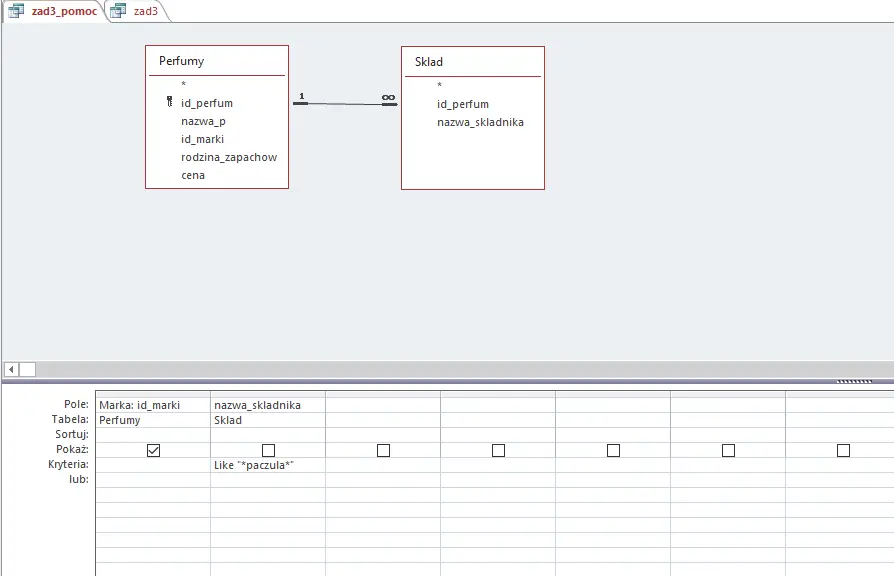
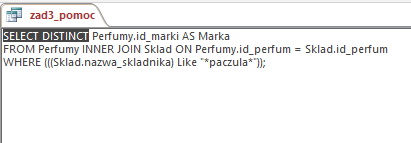
Najpierw stworzymy kwerendę, w której wybierzemy wszystkie marki, które w swoich perfumach posiadają składnik, który w nazwie ma „paczula” — później ze zbioru wszystkich marek usuniemy te wcześniej znalezione. W tej kwerendzie (w widoku SQL) konieczne jest dodanie słowa kluczowego DISCTINCT po słowie SELECT, aby marki nie powtarzały się w wynikach.
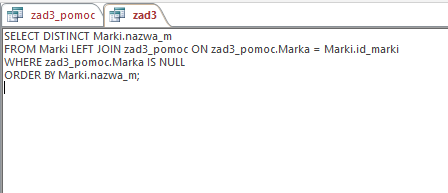
Korzystamy tutaj z języka SQL i LEFT JOIN, które wybiera tylko te marki, których nie ma w poprzedniej kwerendzie.
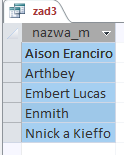
Oto wynik kwerendy i odpowiedź do tego podpunktu.
Zadanie 6 — podpunkt 4

W zadaniu wykorzystamy prostą kwerendę wybierającą nazwy i ceny perfum o określonych warunkach, która od razu przemnoży ceny przez 0.85.Pamiętajmy też o sortowaniu niemalejącym (czyli rosnącym):
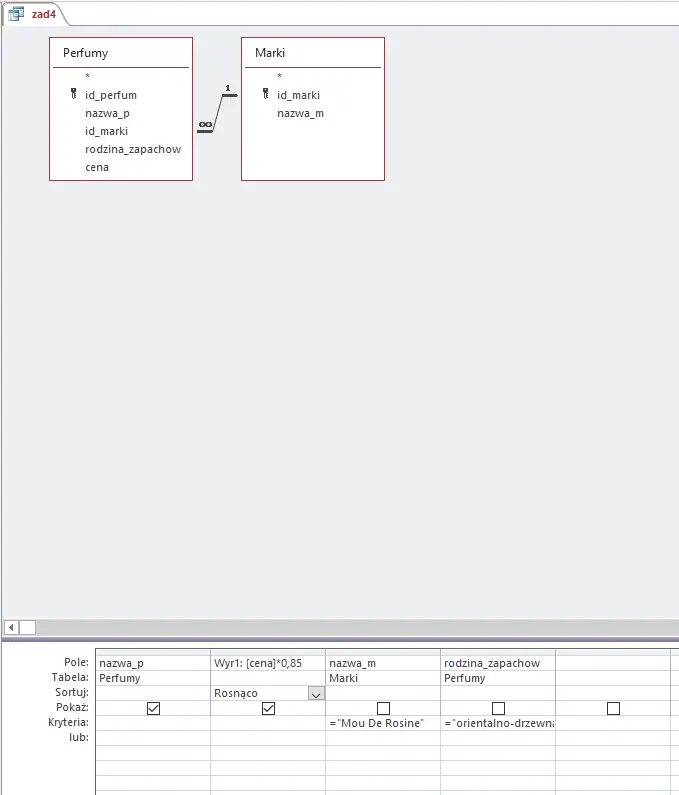
Uruchomienie kwerendy daje nam odpowiedź:
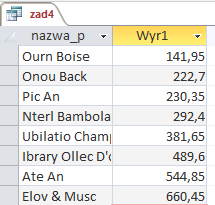
Zadanie 6 — podpunkt 5

Do rozwiązania tego podpunktu stworzymy tym razem dwie pomocnicze kwerendy. Pierwsza zliczy ilość wszystkich perfum dla każdej marki, druga zliczy ilość perfum z danej rodziny dla każdej marki. Ostatnia, finalna kwerenda zestawi dwie powyższe ze sobą dając nam wynik. Wszystkie kwerendy przedstawione są po kolei poniżej (ponownie przypomnę, że aby skorzystać z grupowania/sumowania należy wcisnąć Sumy z zakładki Dane):
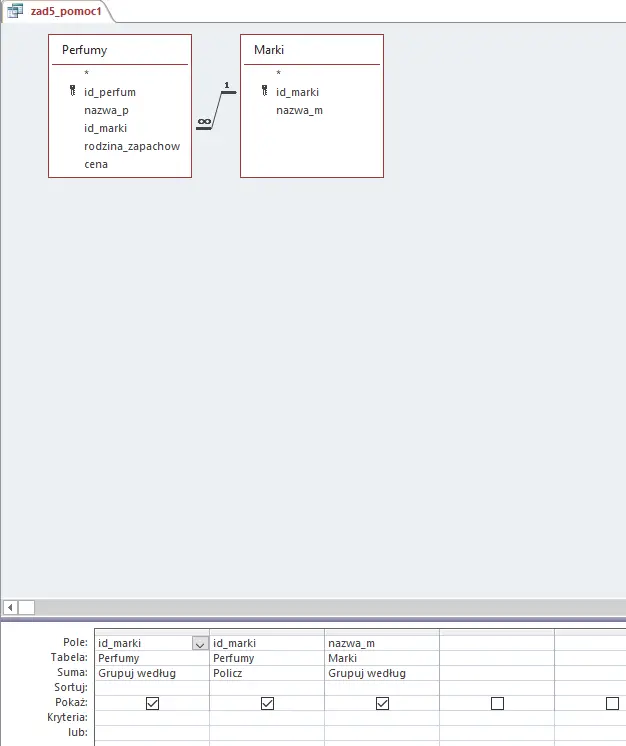
Kwerenda licząca ilość perfum danej marki.
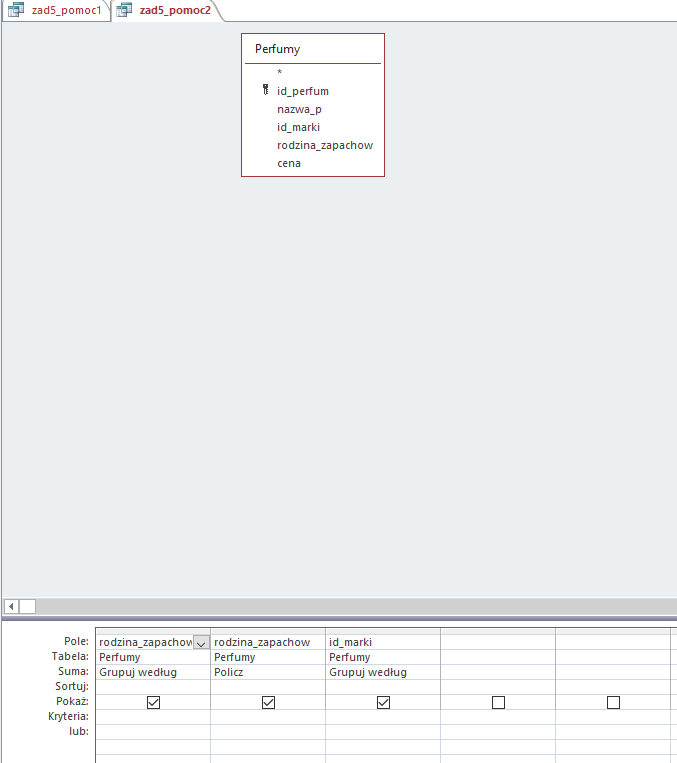
Kwerenda licząca ilość perfum danej rodziny dla każdej marki.
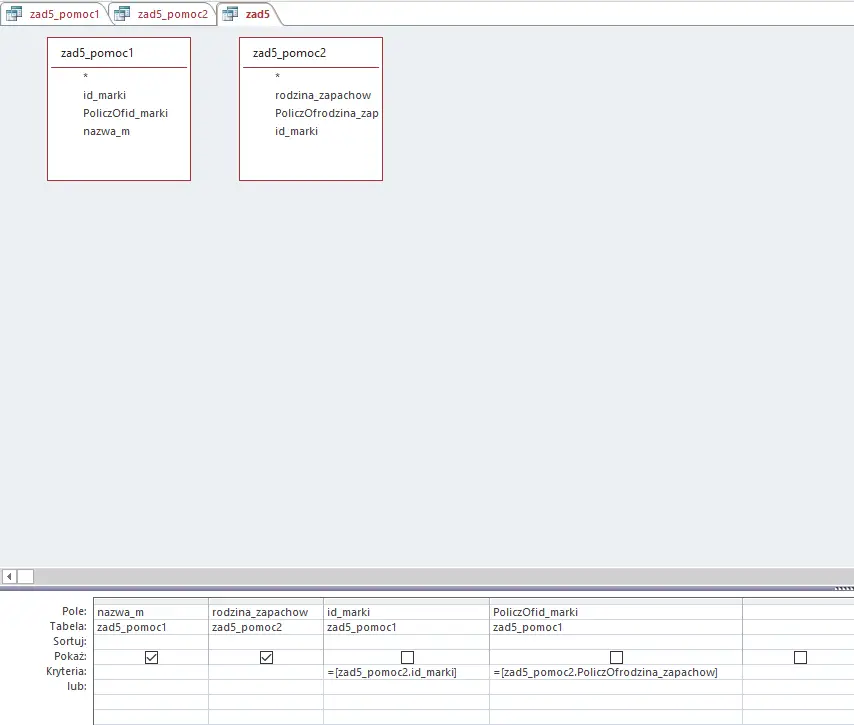
Połączenie dwóch kwerend pomocniczych: jeżeli ilość wszystkich perfum marki jest równa ilości perfum z danej rodziny w tej samej marce, to spełnia ona wymagania z polecenia.
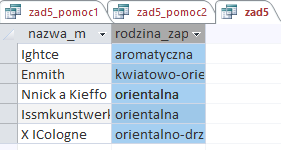
Uruchomienie powyższej kwerendy daje nam odpowiedź:
Mam nadzieję, że dotarliście aż tutaj. Nie zapomnijcie o tym żeby samodzielnie rozwiązać powyższe zadania. Życzyłbym sobie, aby każdy z was mógł sobie wkrótce powiedzieć, ze matura z informatyki 2019 była banalnie prosta. Powodzenia!





