W jednym z poprzednich postów omawialiśmy czym jest największy wspólny dzielnik i jak go w sposób programistyczny wyznaczyć. W ramach serii wpisów o algorytmach dzisiaj omówimy czym jest najmniejsza wspólna wielokrotność dwóch liczb naturalnych, a także jak ją wyznaczyć.
Za najmniejszą wspólną wielokrotność n i k uznajemy taką najmniejszą liczbę, która jest różna od zera i jednocześnie jest wielokrotnością obu liczb. Najmniejsza wspólną wielokrotność dwóch liczb może zostać obliczona, gdy znamy ich największy wspólny dzielnik ze wzoru n*k/NWD(n, k). O tym, jak wyznaczać NWD przeczytasz tutaj.
Choć, raczej nie wygląda to jak w programie komputerowym, to wyszukiwanie NWW wykonujemy np. podczas szukania wspólnego mianownika dodawanych ułamków. Weźmy dla przykładu liczby 36, 60, 210. Dosyć niepraktycznym byłoby ich wymnażanie, bo ich iloczyn wynosi 453 600. Łatwo sobie zatem wyobrazić jak wielkie by były wtedy liczniki. Bardziej praktycznym rozwiązaniem jest wyznaczenie ich NWW, które wynosi 1260. Jak więc wyznaczyć NWW? Poniżej omówimy algorytm, a następnie dokonamy jego implementacji w trzech, dostępnych na maturze językach programowania.
Algorytm wyszukiwania największej wspólnej wielokrotności
Z racji, iż znamy wzór na największą wspólną wielokrotność, możemy go wykorzystać w naszym algorytmie. Znacząca jego część opiera się jednak na algorytmie wyznaczania największego wspólnego dzielnika. Jeżeli więc chcesz dokładniej przeanalizować jego działanie, odsyłam Cię do tego wpisu.
Sam algorytm na wyznaczanie NWW nie jest skomplikowany, gdy mamy już gotowy na NWD. Pobieramy najpierw od użytkownika dwie liczby naturalne dodatnie a oraz b. Następnie obliczamy ich największy wspólny dzielnik i zapisujemy go w zmiennej pomocniczej. Teraz wystarczy już tylko obliczyć iloczyn z a i b. Następnie trzeba podzielić go przez przechowany NWD, a następnie zwrócić wartość. Tak opisany algorytm możemy przedstawić na schemacie blokowym:
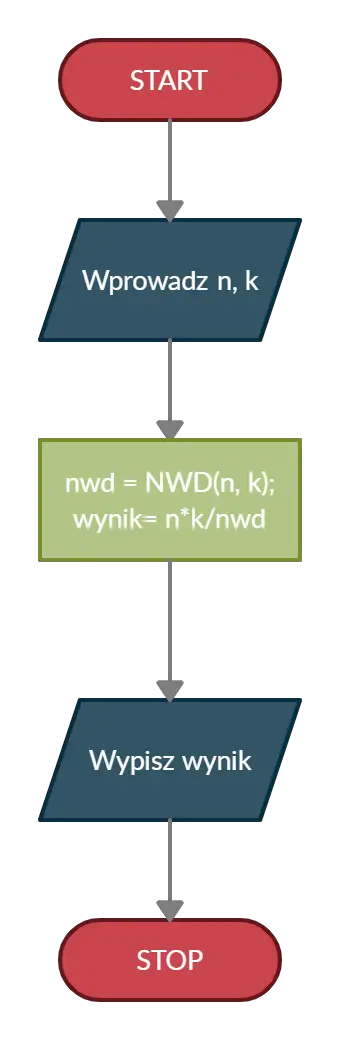
Implementacja wyszukiwania NWW w Javie, C++ oraz Pythonie
Mając już nasz algorytm, możemy użyć go w programie. Zapewne większość z Was, czytelnicy, przygotowuje się właśnie do egzaminu maturalnego z informatyki. Z myślą o Was, tak jak w poprzednich wpisach o algorytmach, przygotowałem trzy implementacje w dostępnych na maturze językach: C++, Java i Python. W każdym z nich użyłem, już wcześniej zaimplementowaną funkcję, liczącą NWD w sposób rekurencyjny. Jeżeli nadal nie wiesz, czym jest rekurencja, to polecam zapoznać się z tym wpisem, w którym wszystko jest wyjaśnione.nww.cpp
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
//program wyliczający NWW dla dwóch liczb //Kosiński Łukasz #include <iostream> using namespace std; unsigned nwd(unsigned a, unsigned b) { unsigned pom= (a>b)?a%b:b%a;// program przypisuje zmiennej pomocniczej resztę z dzielenia większej liczby przez mniejszą if(pom==0)return (a>b)?b:a;//jeśli modulo z dwóch liczb wynosi zero to wynikiem jest mniejsza z nich return (a>b)? nwd(pom,b) : nwd(pom,a);//jeśli modulo jest różne od 0 to program rekurencyjnie wylicza nwd dla zmiennej pom. i mniejszej z liczb } unsigned long long nww(unsigned a, unsigned b) { return a*b/nwd(a,b);//zgodnie ze wzorem na NWW } int main() { unsigned x,y; cin >> x >> y;//wprowadzamy dwie liczby całkowite cout << nww(x,y) << endl; return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
import java.util.Scanner; public class NWW { private static int nwd(int a, int b) { // korzystamy tutaj z metody obliczającej NWD z poprzednich wpisów int c = (a>b) ? a%b : b%a; if(c==0) return (a>b) ? b : a; return (a>b) ? nww(c, b) : nww(c, a); } private static int nww(int a, int b){ int nww = a*b/nwd(a, b); // wykorzystujemy tutaj właściwość, że najmniejsza wspólna wielkrotność dwóch liczb jest równa ich iloczynowi, podzielonemu przez ich największy wspólny dzielnik return nww; } public static void main(String[] args) { Scanner scanner = new Scanner(System.in); // inicjalizujemy Scanner - obiekt, który będzie zczytywał dane od użytkownika System.out.println("Program obliczający najwmniejszą wspólną wielokrotność"); System.out.println("Podaj pierwszą liczbę: "); int a = scanner.nextInt(); // pobieramy zmienną od użytkownika System.out.println("Podaj drugą liczbę: "); int b = scanner.nextInt(); // pobieramy zmienną od użytkownika scanner.close(); // zwalniamy zasoby System.out.println("Najmniejsza wspólna wielokrotność liczb " + a + " i " + b + " to: " + nww(a, b)); // wywołujemy metodę przy drukowaniu wyniku } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
#Wykorzystujemy tutaj utworzony we wczesniejszych postach algorytm NWD def nwd(x, y): #definiujemy funkcje do późniejszego użycia z = x % y if (x > y) else y % x # obliczamy reszte dzielenia z liczb (wykorzystujemy tu wyrażenie warunkowe) if z == 0: return y if (x > y) else x #jeżeli reszta ta jest rowna 0, to wynikiem jest mniejsza z liczb return nwd(z, y) if x > y else nwd(z, x) # w przeciwnym wypadku rekurencyjnie sprawdzamy NWD reszty dzielenia z mniejsza liczba def nww(x, y): #definiujemy kolejna funkcje, ktora bedzie korzystac z NWD return a*b/nwd(x , y) print("Program znajdujacy najmniejsza wspolna wielokrotnosc dwoch liczb") print("Podaj liczbę a: ") a = int(input()) print("Podaj liczbę b: ") b = int(input()) print(nww(a, b)) |
Najmniejsza wspólna wielokrotność — co warto o niej wiedzieć
- Podobnie jak w przypadku NWD, aby obliczyć najmniejszą wspólną wielokrotność więcej niż dwóch liczb, wystarczy obliczyć p=NWW pierwszych dwóch. Następnie NWW dla p i kolejnej liczby i tak dalej, aż dojdziemy do ostatniej liczby.
- Wzór na NWW można przekształcić, przez co możliwe jest obliczenie NWD dwóch liczb, gdy mamy ich największą wspólną wielokrotność: NWD = a*b/NWW(a,b)
- NWW można również obliczyć, mając jedynie kartkę papieru i długopis. Wystarczy rozpisać czynniki obu liczb, wyznaczyć te czynniki, które nie są dla nich wspólne, a następnie obliczyć iloczyn jednej z tych dwóch liczb i czynników, które nie są wspólne z drugiej liczby.
Matura z informatyki coraz bliżej, a Ty nadal nie wiesz jak się do niej przygotować? Rzuć okiem na wpis, w którym omówiłem na co należy najbardziej zwrócić uwagę przy nauce. Znajdziesz też tam inne ważne algorytmy i odnośniki do ich objaśnienia.






Skersony
says:ooo dzieki, elegandzko opisany programik 🙂