Do majowych matur pozostało już niewiele czasu. Po świątecznym odpoczynku maturzyści wzięli się więc pełną parą do przygotowań do egzaminu dojrzałości. Aby nieco ułatwić im to zadanie przygotowaliśmy rozwiązania do próbnej matury z informatyki 2021. Poniżej znajdziecie odpowiedzi, wraz ze szczegółowym omówieniem. Zostańcie z nami 😀 Próbna matura z informatyki, podobnie jak jej majowy odpowiednik, składa się z dwóch części: teoretycznej i praktycznej. W pierwszej z nich do dyspozycji mamy jedynie kartkę, prosty kalkulator, a także długopis. Na zadania z teorii mamy godzinę czasu. Część praktyczna wymaga od nas użycia komputera i dostępnych na nim narzędzi informatycznych, a na wykonanie zadań mamy półtorej godziny. Całość trwa więc 3 i pół godziny. Nie przedłużając jednak, przejdźmy do omawiania arkusza.
Próbna matura z informatyki 2021 rozwiązania – część teoretyczna
Na wstępie mogę śmiało powiedzieć, że w tegorocznej próbnej maturze z informatyki zauważalne jest lekkie obniżenie trudności zadań, które wynika zapewne z wprowadzonych w maturach zmian. Jeżeli jeszcze ich nie sprawdzałeś, to koniecznie zajrzyj do tego wpisu.
W części teoretycznej standardowo możemy spotkać zadanie z problemem wymagającym algorytmicznego podejścia, zadanie z analizą algorytmu, a także zadanie sprawdzające wiedzę teoretyczną.
Próbna matura z informatyki 2021 zadanie 1 – turniej
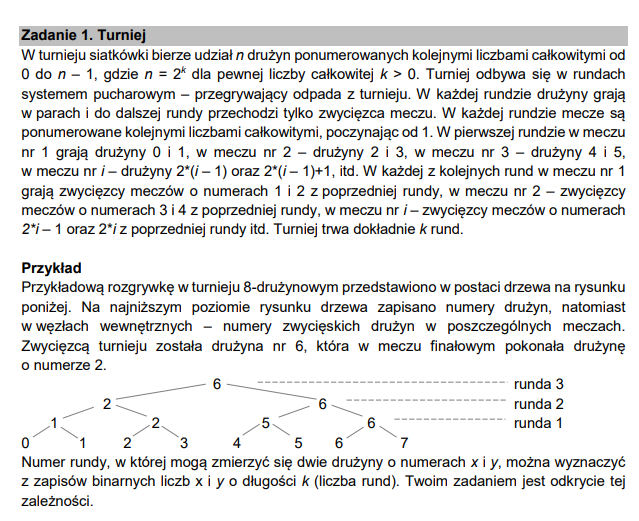
Zadanie dosyć proste. Mamy turniej siatkarski, w którym udział bierze parzysta liczba drużyn. W każdym meczu odpada przegrana drużyna, co oznacza, że z każdą rundą liczba drużyn zmniejsza się dwukrotnie, aż na sam koniec zostaje zwycięzca. Schemat ten sprawdza się dla dowolnej, parzystej liczby drużyn.
Podpunkt 1
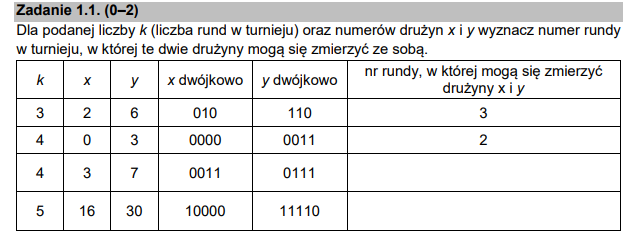
CKE od razu podsuwa nam pomysł na rozwiązanie – w poleceniu możemy wyczytać, że numer rundy jest zależny od binarnego zapisu numeru drużyny x i drużyny y. Dodatkowo w tabeli liczby te zostały zapisane w tymże systemie. Totalna utopia – CKE podaje pomysły na tacy, czego chcieć więcej?
Musimy więc znaleźć zależność pomiędzy binarnymi numerami drużyn. Zapiszmy więc informacje, które znamy: dane z tabeli, a także te z przykładowej drabinki, którą nam wcześniej podano.
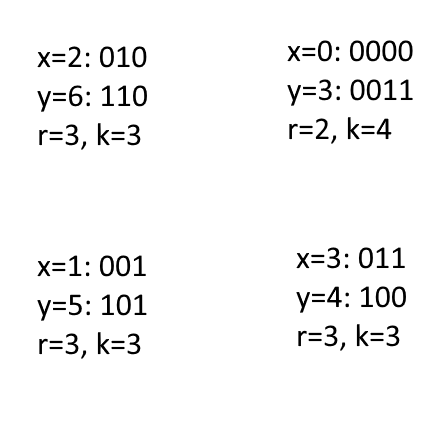
Jak widać odpadają od razu jakiekolwiek operacje arytmetyczne lub logiczne na liczbach binarnych. Przyjrzyjmy się jednak czym różnią się liczby drużyn. Gdyby czytać je od lewej strony, to możemy wskazać w jakim stopniu się one ze sobą pokrywają, tzn. ile mają wspólnych początkowych bitów. Patrząc od lewej zaczynamy porównywać bity i jeśli natrafimy na jakikolwiek bit który nie jest taki sam to przerywamy liczenie:

Widzicie już zależność? Runda, w której dane drużyny się spotkają, jest ściśle zależna od ilości wspólnych bitów zapisów binarnych numerów drużyn, a także od ilości wszystkich rund. Zależność tą możemy wyrazić wzorem:
r = k – w
Gdzie r to numer rundy w której drużyny się spotkają, k to ilość wszystkich rund, a w to liczba pokrywających się pierwszych bitów dla zapisów binarnych. Znając już więc zależność możemy uzupełnić tabelę:
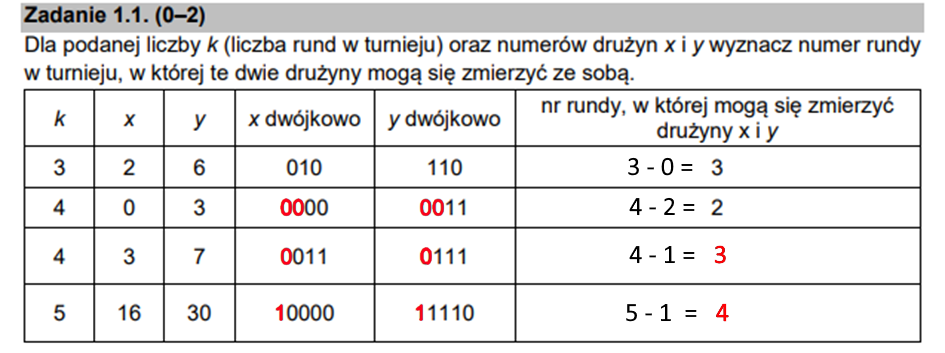
Podpunkt 2

Naszym zadaniem jest teraz stworzenie uniwersalnego algorytmu, który dla dowolnych x y k obliczy rundę, w której spotkają się obie drużyny. Jak już wiemy z poprzedniego podpunktu, sytuacja ta jest zależna od ilości początkowych bitów w zapisie binarnym numerów drużyn. Wystarczy więc zamienić x i y na postać binarną, a następnie porównać pierwsze ich znaki.
Ja proponuje jednak nieco szybsze i sprytniejsze rozwiązanie. Zamiast zamieniać obie liczby na postać binarną (co wymaga użycia dwóch pętli), a następnie je porównywać (co wymaga kolejnej pętli), wystarczy pobierać kolejne bity z obu liczb (poprzez operator modulo) i od razu je porównywać – wszystko w jednej pętli. Zerknijcie na pseudokod:
pom = 0 //definiujemy zmienna pomocnicza
powtórz k razy: //iterujemy k-razy – tyle bitow maja nasze liczby
jeżeli x%2 == y%2: //jezeli w danym miejscu obie liczby maja taki sam bit
pom += 1 //to zwiekszamy zmienna pomocnicza o 1
w przeciwnym wypadku: //w innym wypadku
pom = 0 //zerujemy zmienna pomocnicza – dzieki temu obliczymy ilosc zmiennych na poczatku
x = x div 2 //dzielimy calkowicie x przez 2
y = y div 2 //dzielimy calkowicie y przez 2
wypisz (k – pom) //drukujemy wynik: ilosc rund – ilosc wspolnych bitow na poczatku
Sprawdzamy liczby x i y od prawej strony, co oznacza, że musimy zerować zmienną pomocniczą za każdym razem, gdy trafimy na różne bity. Dzięki temu na sam koniec działania pętli dostaniemy ilość początkowych bitów, które są takie same dla obu liczb.
Próbna matura z informatyki 2021 zadanie 2 – analiza algorytmu

To zadanie było już nieco cięższe. Na pierwszy rzut oka wydawać by się mogło, że algorytm ten nie ma jakiegoś konkretnego celu – zwyczajna łamigłówka. Sprytniejsze oko zauważy jednak, że jest to uproszczona implementacja metody Newtona-Raphsona, którego omówienie i implementacje znajdziecie w tym miejscu. Metoda ta pozwala na obliczenie wartości pierwiastka kwadratowego z danej liczby ze wskazaną precyzją. Pętla będzie wykonywać się dopóki k – p > 1, co oznacza, że 1 jest naszą precyzją. Oznacza to, że wszelkie pierwiastki będą miały wyłącznie wartość całkowitą – przykładowo liczba 3 nie da wyniku ~ 1,73, a 1. Oto schemat blokowy powyższego algorytmu:
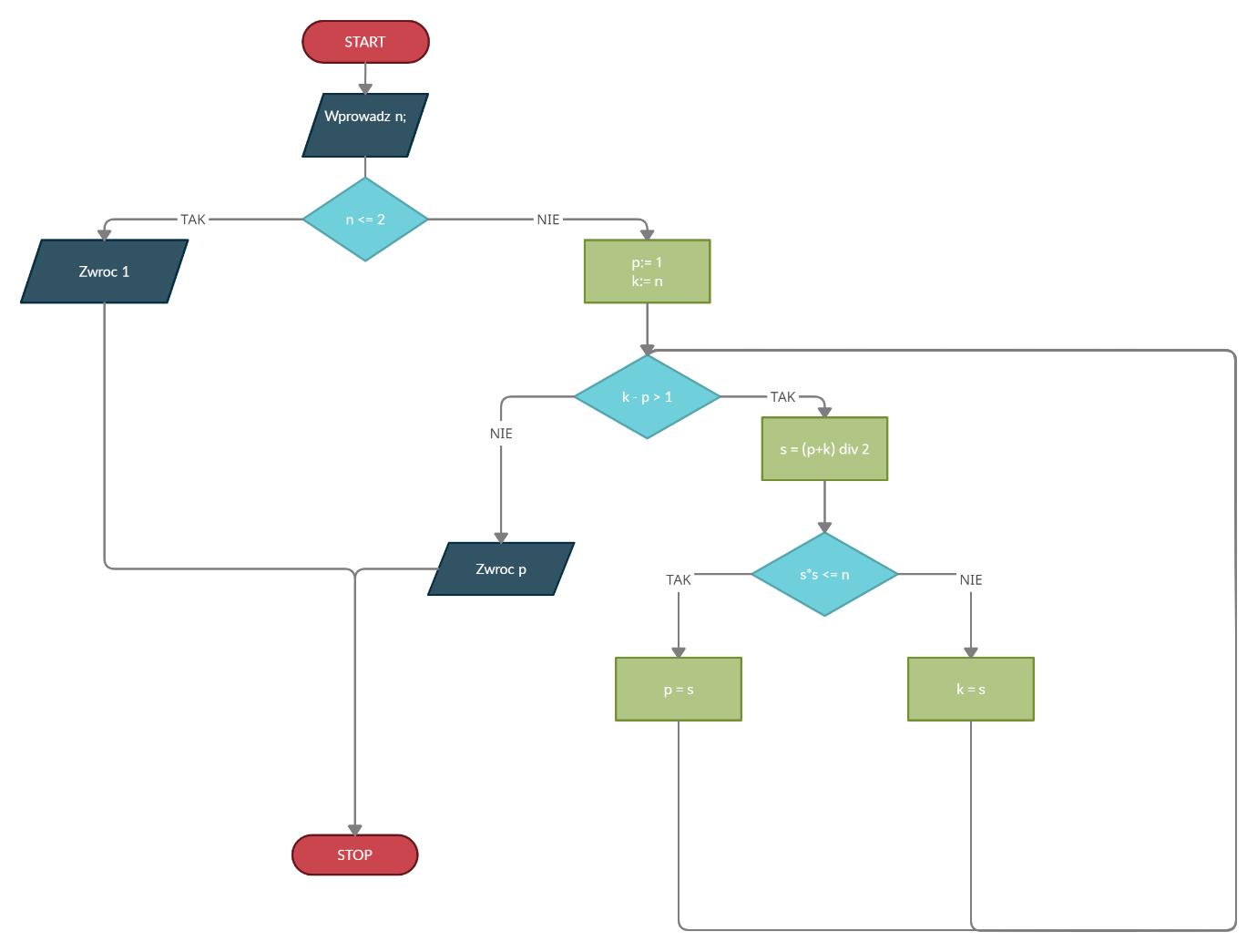
Wiedząc już na czym polega algorytm możemy przystąpić do rozwiązywania podpunktów.
Podpunkt 1

Wiemy już, że algorytm oblicza całkowitą wartość pierwiastka kwadratowego z danej liczby. Skąd wiemy jaka ona jest? Z matematyki na pewno pamiętacie zależność, że 2=(pierwiastek z 4) < (pierw. Z 5) < (pierw. z 9) = 3. Łatwo więc wywnioskować, że wynikiem działania algorytmu będzie wartość największej liczby mniejszej od n, z której pierwiastek jest całkowity. Tak więc tabela powinna zostać uzupełniona w ten sposób:
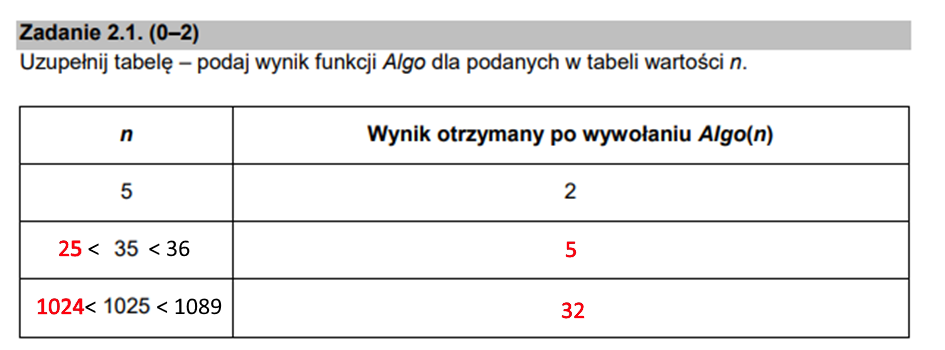
Podpunkt 2

W tym podpunkcie nie pozostaje niestety nic innego, jak prześledzenie ilości iteracji pętli dla każdej z tych wartości. Całe szczęście mamy miejsce na obliczenia pod zadaniem, a także brudnopis na końcu arkusza. Poprawnie uzupełniona tabelka powinna wyglądać następująco:
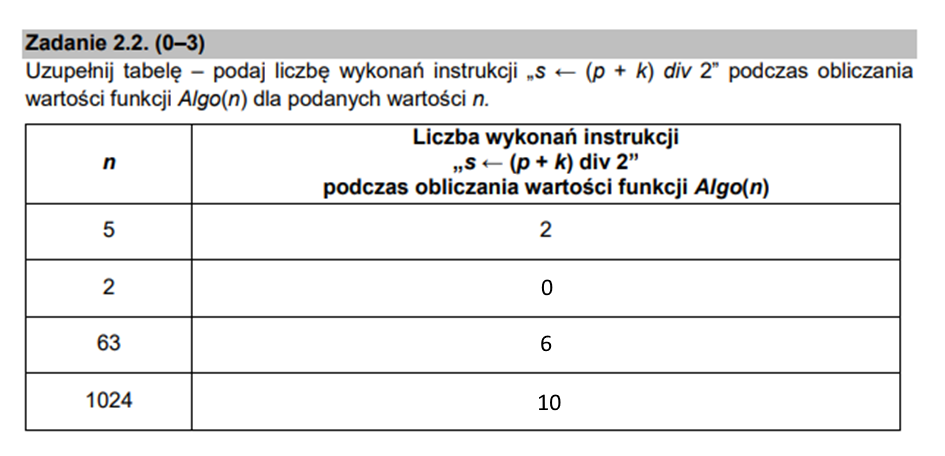
Próbna matura z informatyki 2021 zadanie 3 – pytania zamknięte
Zadanie trzecie składa się z 4 zamkniętych podpunktów. Uwaga na pomyłki. Udzielenie złej odpowiedzi w jakiejkolwiek części podpunktu oznacza zero za cały podpunkt.
Podpunkt 1
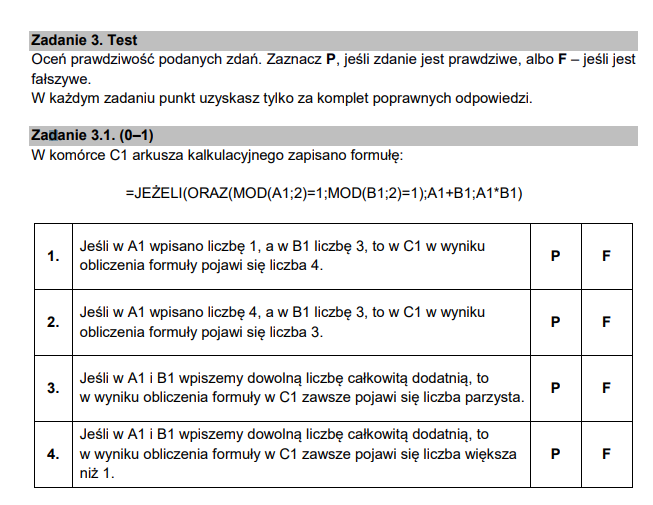
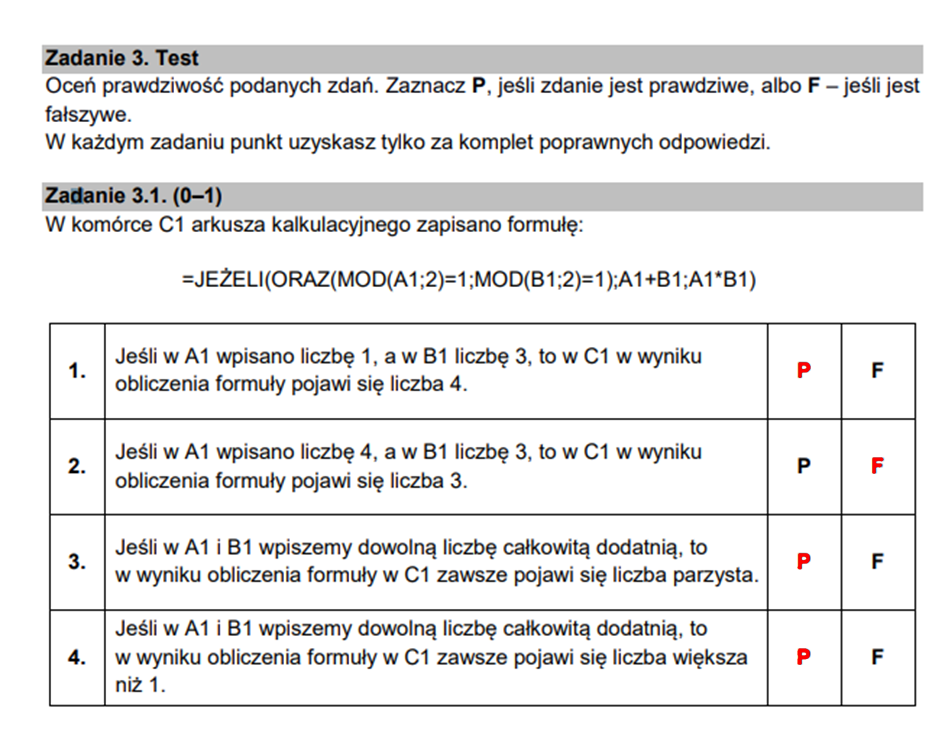
Przeanalizujmy powyższą formułę. Funkcja MOD działa jak modulo – zwraca resztę z dzielenia pierwszego argumentu przez drugi. Formuła ta zwróci więc sumę obu liczb, jeżeli obie są nieparzyste. W każdym innym wypadku formuła zwróci ich iloczyn. Znając działanie algorytmu łatwo więc odpowiedzieć na dwa pierwsze pytania – w pierwszym wypadku mamy dwie nieparzyste cyfry, więc wynikiem jest ich suma. W drugim wypadku mamy 4 i 3 – w wyniku powinno więc wyjść 12. Zastanówmy się nad dwoma pozostałymi pytaniami. Rozważmy wszystkie przypadki, dla całkowitych dodatnich A1 B2:
- A1 parzysta, B1 nieparzysta, wynik: ich iloczyn, a skoro jedna z nich jest parzysta, to wynik również będzie parzysty, ponieważ liczbę parzystą możemy zapisać jako 2n, a nieparzystą jako 2m + 1, to ich iloczyn wyniesie 4mn + 2n = 2(2mn + 1) – liczbę podzielną przez 2.
- A1 nieparzysta, B1 nieparzysta: suma. Suma dwóch liczb nieparzystych daje zawsze liczbę parzystą, ponieważ pierwszą liczbę nieparzystą możemy zapisać jako 2n + 1, a drugą jako 2m + 1, to ich suma da 2m + 2n + 2 = 2(m + n + 1) – liczbę podzielną przez 2.
- A1 nieparzysta, B2 parzysta – to samo co w pierwszym przypadku
Udowodniliśmy więc, że wynik formuły będzie zawsze parzysty. Czy wynik ten będzie zawsze większy od 1? Okazuje się, że tak. Spójrzcie na wzory. W każdym z przypadków otrzymujemy wynik suma/iloczyn niewiadomych + 1. Taka liczba by była mniejsza lub równa jeden, gdy suma/iloczyn niewiadomych by były mniejsze lub równe zero, a z zadania wynika że liczby A1 I B2 są całkowite > 0. Uzupełniamy więc tabelę:
Podpunkt 2

W podpunkcie tym wszystko raczej jasne – zwyczajna operacja logiczna na dwóch bitach. Całe wyrażenie zwróci 1, jeżeli oba nawiasy będą równe 1. Pierwszy nawias będzie równy jeden, gdy wewnętrzny zero, wewnętrzny będzie równy 0, gdy a = 1 i b = 1. Drugi nawias będzie równy jeden, gdy wewnętrzny będzie równy 0, wewnętrzny będzie równy zero, gdy a=1 i b=1. Podsumowując podane wyrażenie zwróci 1 wtedy, gdy oba wejścia są równe 1, w pozostałych wypadkach zwróci 0.

Podpunkt 3

W podpunkcie tym najprościej jest po prostu zamienić wartości binarne na dziesiętne:

Podpunkt 4
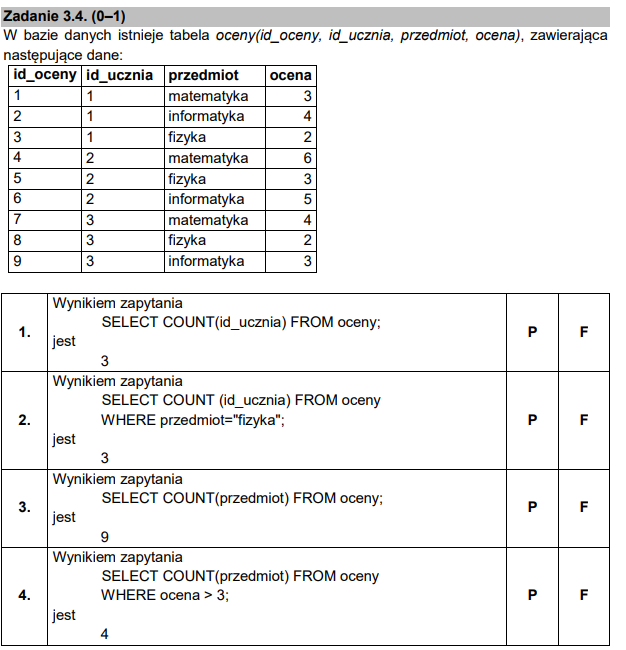
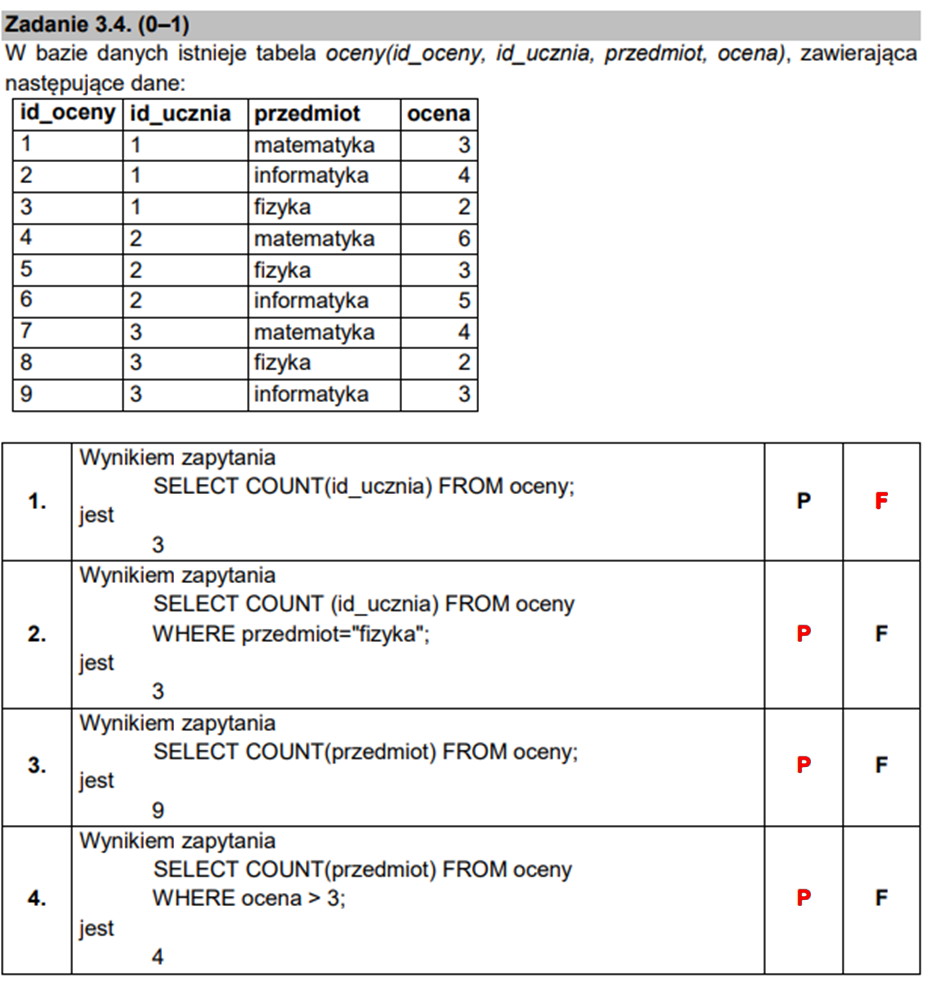
Nie mogło zabraknąć wiedzy z SQL. W podpunkcie tym trzeba było uważać na pułapkę zastawioną przez CKE. Funkcja agregująca COUNT nie zlicza unikalnych wartości – zlicza je wszystkie dla danego warunku.
Próbna matura z informatyki 2021 rozwiązania – część praktyczna
Praktyka jest niewątpliwie trudniejszą częścią egzaminu maturalnego z informatyki, trzeba tutaj bowiem wykazać się umiejętnością rozwiązywania bardziej złożonych problemów, a co więcej jesteśmy ograniczeni przez czas. Próbna matura nie jest tutaj wyjątkiem. Przejdźmy zatem do rozwiązywania drugiej części próbnej matury z informatyki.
Próbna matura z informatyki 2021 zadanie 4 – galerie handlowe

Zadanie to narzuca nam użycie napisanego przez nas programu. Oznacza to, że użycie jakiegokolwiek innego sposobu z automatu daje nam 0 punktów – nawet, jeżeli wynik jest poprawny. W kolejnych podpunktach przedstawimy więc rozwiązania w trzech dostępnych na maturze językach: C++, Javie oraz Pythonie. Pamiętajcie również, że możecie sprawdzić działanie waszego programu otwierając plik „galerie_przyklad.txt” i porównując jego wynik z podanym przez CKE.
Podpunkt 1

W podpunkcie tym najłatwiej będzie stworzyć mapę zawierająca nazwę kraju jako klucz oraz liczbę miast jako wartość. Następnie wystarczy przeiterować plik wiersz po wierszu, sprawdzając, czy dane państwo znajduje się w mapie. Jeżeli nie, to je dodajemy, w przeciwnym wypadku zwiększamy po prostu przypisaną krajowi ilość miast o jeden. Na koniec iterujemy poprzez obiekt mapy, drukując wynik zadania do pliku wyjściowego. Co ciekawe to pierwszy raz, gdy CKE oczekuje zapisania danych wyjściowych programu do pliku.
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
#include <iostream> #include <fstream> #include <map> //wymagany import!! using namespace std; bool isNumber(string s){ //funckja pomocnicza, sprawdzajaca czy dany tekst jest liczba for(char c : s){ //jezeli chociaz jeden znak w tekscie nie bedzie cyfra if(!isdigit(c)){ return false; //to oznacza ze tekst nie jest liczba } } return true; //w przecwinym wypadku tekst jest liczba } int main() { fstream file; ofstream solution("C:\\wynik4_1.txt"); //otwieramy plik wyjsciowy file.open("galerie.txt", ios_base::in); //otwieramy plik zrodlowy if(!file || !solution){ //jezeli nie uda sie otworzyc ktoregokolwiek z pliku, zwroc blad perror("Nie udalo sie otworzyc plikow"); return 1; } map<string, int> map; //tworzymy mape przechowujaca panstwa i ilosc miast string s; //zmienna przechowujaca wyraz bool isCountryCode = true; //zmienna pomocnicza sprawdzajaca czy aktualny tekst jest symbolem panstwa string country; //zmienna przechowujaca nazwe aktualnego panstwa while(file >> s){ //zczytujemy wszystkie pojedyncze wyrazy do if(!isNumber(s)){ //jezeli tekst nie jest liczba if(isCountryCode){ //sprawdzamy czy jest to kod kraju country = s; //jezeli tak, to go zapisujemy if(map.find(s) == map.end()){ //jezeli nie ma takiego panstwa w mapie, dodajemy je map[country] = 0; } isCountryCode = false; //przelaczamy zmienna na false - nastepny tekst bedzie nazwa miasta } else { map[country]++; //natrafilismy na miasto, wiec zwiekszamy ilosc miast w panstwie o 1 isCountryCode = true; //przelaczamy zmienna na true - nastepny tekst bedzie kodem panstwa } } else { continue; //nie sprawdzamy pomieszczen w tym podpunkcie - pomijamy liczb } } file.close(); //na koniec zamykamy plik for (auto const& element : map){ //zapisujemy wynik dzialania programu do pliku wyjsciowego solution << element.first << " " << element.second << endl; } solution.close(); //na koniec zamykamy plik system("pause"); return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
package matura; import java.io.BufferedReader; import java.io.BufferedWriter; import java.io.File; import java.io.FileReader; import java.io.FileWriter; import java.util.HashMap; import java.util.Map.Entry; public class Main { public static void main(String[] args) { try { //otaczamy kod w try/catch - dzieki temu wszelkie bledy z plikami zostana zraportowane File f = new File("C://galerie.txt"); //wskazujemy sciezke pliku zrodlowego BufferedReader br = new BufferedReader(new FileReader(f)); //otwieramy plik przy uzyciu BufferedReader i FileReader, aby moc z niego czytac File f2 = new File("C://java/wynik4_1.txt"); //wskazujemy sciezke pliku wyjsciowego if(!f2.exists()) { f2.createNewFile(); //tworzymy plik, jeżeli nie istnieje } BufferedWriter wr = new BufferedWriter(new FileWriter(f2)); //otwieramy plik przy uzyciu BufferedWriter i FileWrited, aby moc do niego zapisywac String line; //zmienna pomocnicza przechowujaca aktualny wiersz HashMap<String, Integer> citiesMap = new HashMap<String, Integer> (); //mapa przechowujaca panstwa i liczbe miast while((line = br.readLine()) != null) { //dopoki nie napotkamy konca pliku String country = line.split(" ")[0]; //pobieramy nazwe panstwa z aktualnej linijki - dzielimy ja spacjami i wybieramy pierwszy wyraz if(citiesMap.containsKey(country)) { //jezeli panstwo jest juz zapisane citiesMap.put(country, citiesMap.get(country) + 1); //zwiekszamy ilosc miast w nim o 1 } else { citiesMap.put(country, 1); //w przeciwnym wypadku dodajemy je do mapy } } br.close(); //po zakonczonej pracy z plikiem nalezy go zamknac for(Entry<String, Integer> entry : citiesMap.entrySet()) { wr.write(entry.getKey() + " " + entry.getValue() + "\n"); //zapisujemy wszystkie wartosci z mapy } wr.close(); //po zakonczonej pracy z plikiem nalezy go zamknac } catch (Exception e) { e.printStackTrace(); } } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
inputFile = open("C:\\galerie.txt", "r") #otwieramy plik zrodlowy w trybie read outputFile = open("C:\\python\\wynik4_1.txt", "w") #otwieramy plik wyjsciowy w trybie write countries = {} #tworzymy mape przechowujaca nazwy panstw i ilosc miast for line in inputFile: #iterujemy poprzez kazdy wiersz w pliku zrodlowym country = line.split(" ")[0] #pobieramy pierwszy wyraz - nazwe panstwa if countries.__contains__(country): #jezeli to panstwo jest juz zapisane countries[country] += 1 #zwiekszamy ilosc maist o 1 else: countries[country] = 1 #w przeciwnym wypadku zapisujemy je for country in countries: #nastepnie iterujemy poprzez wyniki outputFile.write(country + " " + str(countries[country]) + "\n") #zapisujemy je do pliku inputFile.close() #zamykamy plik zrodlowy outputFile.close() #zamykamy plik wyjsciowy |
Wynikiem działania programów powinno być:
A 1
B 1
BG 1
CZ 1
D 15
DK 1
E 6
F 2
FIN 1
GB 5
GR 1
H 1
HR 1
I 6
IRL 1
LT 1
LV 1
NL 2
RO 1
S 1
Podpunkt 2


W podpunkcie tym musimy obliczyć łączną powierzchnie każdej z galerii, a także ilość znajdujących się w niej lokali. Dodatkowo musimy ze wszystkich miast wybrać to, które ma najmniejszą oraz największą powierzchnię całkowitą. W tym celu dobrym pomysłem jest stworzenie oddzielnej klasy/struktury, która przechowa nam informacje o wymiarach lokalu. Następnie iterując poprzez wiersze stworzymy instancje obiektu lokalu, aby zawrzeć w nim informacje na temat aktualnego lokalu. Jednocześnie możemy również policzyć całkowitą powierzchnie danej galerii, a także zapisać ją, jeżeli jej pole jest dotychczas największe/najmniejsze. Mogłoby się wydawać, że użycie oddzielnej klasy/struktury jest tu zbyteczne, jednak pozwala na lepszą organizację danych, a także przyda nam się ona w następnym podpunkcie.
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 |
#include <iostream> #include <fstream> using namespace std; struct Room{ //tworzymy strukture pomocnicza, przechowujaca dane o pomieszczeniach int x = -1; int y = -1; }; bool isNumber(string s){ //funckja pomocnicza, sprawdzajaca czy dany tekst jest liczba for(char c : s){ //jezeli chociaz jeden znak w tekscie nie bedzie cyfra if(!isdigit(c)){ return false; //to oznacza ze tekst nie jest liczba } } return true; //w przecwinym wypadku tekst jest liczba } int main() { fstream file; ofstream solutionA("C:\\wynik_4_2a.txt"), solutionB("C:\\wynik_4_2b.txt"); //otwieramy pliki wyjsciowe w trybie in file.open("galerie.txt", ios_base::in); //otwieramy plik zrodlowy if(!file || !solutionA || !solutionB){ //jezeli nie uda sie otworzyc ktoregokolwiek z pliku, zwroc blad perror("Nie udalo sie wczytac plikow"); return 1; } string s, city, maxAreaCity, minAreaCity; //tworzymy zmienne pomocnicze przechowujace nazwy aktualnego miasta, maista o najwiekszej powierzchni i o najmniejszej powierzchni bool isCity = false; //zmienna pomocnicza Room currentRoom; //aktualne pomieszczenie int totalArea = 0; //calkowita powierzchnia int totalRooms = 0; //ilosc wszystkich pomieszczen int minTotalArea = INT_MAX; //najmniejsza powierzchnia int maxTotalArea = -1; //najwieksza powierzchnia while(file >> s){ //zczytujemy wszystkie wyrazy do zmiennej s if(s == "0"){ //jezeli natrafimy na 0, - czyli koniec pomieszczen, kontynuujemy continue; } else if(!isNumber(s)){ //jezeli wyraz nie jest liczba if(!isCity){ //jezeli nie jest miastem, to pomijamy go i przelaczamy zmienna pomocznicza - nastepny wyraz bedzie nazwa miasta isCity = true; continue; } else { //jezeli natrafilismy na miasto if(totalArea != 0){ //zapisujemy dane poprzedniego miasta do pliku solutionA << city << " " << totalArea << " " << totalRooms << endl; if(totalArea > maxTotalArea){ //sprawdzamy tez, czy jego pole jest wieksze od max maxTotalArea = totalArea; maxAreaCity = city; } if(totalArea < minTotalArea){ //sprawdzamy, czy jego pole jest mniejsze od min minTotalArea = totalArea; minAreaCity = city; } } city = s; //w przeciwnym wypadku resetujemy zmienne totalArea = 0; totalRooms = 0; isCity = false; } }else{ if(currentRoom.x == -1){ //jezeli nie mamy jeszcze pierwszego wymiaru currentRoom.x = stoi(s); //ustawiamy go }else { totalArea += currentRoom.x * stoi(s); //w przeciwnym wypadku liczymy pole i dodajemy je do powierzchni calkowitej totalRooms++; currentRoom = Room(); } } } if(totalArea != 0){ //musimy jeszcze sprawdzic ostatnie miasto solutionA << city << " " << totalArea << " " << totalRooms << endl; if(totalArea > maxTotalArea){ maxTotalArea = totalArea; maxAreaCity = city; } if(totalArea < minTotalArea){ minTotalArea = totalArea; minAreaCity = city; } } solutionB << maxAreaCity << " " << maxTotalArea << endl; //na koniec zapisujemy wyniki do pliku b: solutionB << minAreaCity << " " << minTotalArea << endl; //zapisujemy najwieksze i najmniejsze miasto file.close(); //zamykamy wszystkie pliki solutionA.close(); solutionB.close(); system("pause"); return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 |
package matura; import java.io.BufferedReader; import java.io.BufferedWriter; import java.io.File; import java.io.FileReader; import java.io.FileWriter; public class Zad2 { public static void main(String[] args) { try { //otaczamy kod w try/catch - dzieki temu wszelkie bledy z plikami zostana zraportowane File f = new File("C://galerie.txt"); //wskazujemy sciezke pliku zrodlowego BufferedReader br = new BufferedReader(new FileReader(f)); //otwieramy plik przy uzyciu BufferedReader i FileReader, aby moc z niego czytac File f2 = new File("C://java/wynik4_2a.txt"); //wskazujemy sciezke pliku wyjsciowego a File f3 = new File("C://java/wynik4_2b.txt"); //wskazujemy sciezke pliku wyjsciowego b if(!f2.exists()) { f2.createNewFile(); //tworzymy plik a, jeżeli nie istnieje } if(!f3.exists()) { f3.createNewFile(); //tworzymy plik b, jeżeli nie istnieje } BufferedWriter wr = new BufferedWriter(new FileWriter(f2)); //otwieramy plik a przy uzyciu BufferedWriter i FileWrited, aby moc do niego zapisywac String line; //zmienna pomocnicza przechowujaca aktualny wiersz int total = 0; //zmienna pomocnicza przechowujaca calkowita powierzchnie aktualnej galerii int max = Integer.MIN_VALUE; //zmienna pomocnicza przechowujaca najwieksza powierzchnie String maxCity = ""; //zmienna pomocnicza przechowujaca miasto z galeria o najwiekszej powierzchni int min = Integer.MAX_VALUE; //zmienna pomocnicza przechowujaca najmniejsza powierzchnie String minCity = ""; //zmienna pomocnicza przechowujaca miasto z galeria o najmniejszej powierzchni String city = ""; //zmienna pomocnicza przechowujaca aktualne miasto int roomsCount = 0; //zmienna pomocnicza przechowujaca ilosc pomieszcen w aktualnej galerii while((line = br.readLine()) != null) { //dopoki nie napotkamy konca pliku if(total > 0) { //jezeli mamy juz powierzchnie jakies galerii wr.write(city + " " + total + " " + roomsCount + "\n"); //zapisujemy ja do pliku a, wraz z iloscia pomieszczen if(total > max) { //jezeli jej powierzchnia jest wieksza od maksymalnej maxCity = city; //zapisujemy jej dane max = total; } if(total < min) { //jezeli jej powierzchnia jest wmniejsza od minimalnej minCity = city; //zapisujemy jej dane min = total; } } String[] splitted = line.split(" "); //dzielimy wiersz spacjami city = splitted[1]; //pobieramy nazwe miasta - drugi wyraz total = 0; //resetujemy zmienne roomsCount = 0; //pomocnicze int x = -1; //ustawiamy zmienna pomocnicza przechowujaca pierwszy wymiar pomieszczenia - wartosc ujemna oznacza, ze jeszcze takiej nie znalezlismy for(int i=2; i < splitted.length; i++) { //petla wewnetrzna iterujaca poprzez wszystkie liczby w wierszu if(x == -1) { //jezeli jeszcze nie mamy pierwszego wymiaru x = Integer.parseInt(splitted[i]); //zapisujemy go if(x == 0) //jezeli napotkalismy 0 - koniec pomieszczen { break; //przerywamy dzialanie wewnetrznej petli } } else { //jezeli mamy juz x total += x * Integer.parseInt(splitted[i]); //mnozymy go przez aktualny wymiar i dodajemy wynik do powierzhchni calkowitej roomsCount++; //zwiekszamy ilosc pomieszczen o 1 x = -1; //resetujemy pierwszy wymiar } } } if(total > 0) { //po dzialaniu petli rowniez nalezy sprawdzic ostatnie miasto: wr.write(city + " " + total + "\n"); if(total > max) { maxCity = city; max = total; } if(total < min) { minCity = city; min = total; } } br.close(); //po zakonczonej pracy z plikiem nalezy go zamknac wr.close(); //po zakonczonej pracy z plikiem a nalezy go zamknac wr = new BufferedWriter(new FileWriter(f3)); //otwieramy plik a przy uzyciu BufferedWriter i FileWrited, aby moc do niego zapisywac wr.write(maxCity + " " + max + "\n"); //zapisujemy miasto o najwiekszej powierzchni wr.write(minCity + " " + min + "\n"); //zapisujemy miasto o najmniejszej powierzchni wr.close(); } catch (Exception e) { e.printStackTrace(); } } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
inputFile = open("C:\\galerie.txt", "r") #otwieramy plik zrodlowy w trybie read outputFile = open("C:\\python\\wynik4_2a.txt", "w") #otwieramy plik wyjsciowy a w trybie write outputFile2 = open("C:\\python\\wynik4_2b.txt", "w") #otwieramy plik wyjsciowy b w trybie write maxCityName = "" #zmienna przechowujaca nazwe miasta o najwiekszej powierzchni maxCity = -1 #zmienna przechowujaca najwieksza powierzchnie minCity = 9999999 #zmienna przechowujaca najmniejsza powierzchnie minCityName = "" #zmienna przechowujaca nazwe miasta o najmniejszej powierzchni for line in inputFile: #iterujemy poprzez kazdy wiersz w pliku zrodlowym total = 0 #tworzymy zmienne pomocnicze roomsCount = 0 #przechowujace dane o aktualnym miescie splitted = line.split(" ") #dzielimy wiersz na pojedyncze wyrazy city = splitted[1] #pobieramy drugi wyraz - nazwe miasta x = -1 #stawiamy zmienna pomocnicza przechowujaca pierwszy wymiar pomieszczenia - wartosc ujemna oznacza, ze jeszcze takiej nie znalezlismy for i in range(2, len(splitted)): #iterujemy poprzez wszystkie wymiary w wierszu if x == -1: #jezeli nie mamy jeszcze pierwszego wymiaru x = int(splitted[i]) #zapisujemy go if x == 0: #jezeli napotkamy 0 break #przerywamy dzialanie wewnetrznej petli else: #w przeciwnym wypadku total += x * int(splitted[i]) #dodajemy pole do calkowitej powierzchni roomsCount += 1 #zwiekszamy ilosc pomeiszczenm x = -1 #resetujemy pierwszy wymiar outputFile.write(city + " " + str(total) + " " + str(roomsCount) + "\n") #po zliczeniu pola zapisujemy je w pliku a if maxCity < total: #jezeli galeria miala wieksza powierzchnie niz ta najwieksza maxCity = total #zapisujemy jej dane maxCityName = city if minCity > total: #jezeli galeria miala mniejsza powierzchnie niz ta najmniejsza minCityName = city #zapisujemy jej dane minCity = total outputFile2.write(maxCityName + " " + str(maxCity) + "\n") #na koniec zapisujemy najwieksze outputFile2.write(minCityName + " " + str(minCity) + "\n") #i najmniejsze miasto do pliku b inputFile.close() #zamykamy plik zrodlowy outputFile.close() #zamykamy plik wyjsciowy a outputFile2.close() #zamykamy plik wyjsciowy b |
Wynikiem działania algorytmu powinno być:
Londyn 3628 58
Berlin 3777 59
Madryt 2217 34
Rzym 3678 51
Paryz 3889 62
Bukareszt 1957 33
Wieden 2694 42
Hamburg 3518 52
Budapeszt 3598 64
Barcelona 4059 60
Monachium 1734 31
Mediolan 1958 35
Sofia 3631 59
Praga 2622 40
Bruksela 4316 64
Birmingham 1826 25
Kolonia 2104 31
Neapol 3352 48
Turyn 2646 39
Marsylia 3444 56
Sztokholm 2133 33
Walencja 3981 68
Zagrzeb 2177 31
Leeds 2952 44
Amsterdam 3371 60
Sewilla 4305 70
Ryga 1745 30
Frankfurt 3515 57
Palermo 2733 43
Ateny 4435 65
Saragossa 3480 50
Genua 3386 56
Stuttgart 1718 32
Dortmund 3697 57
Rotterdam 3184 49
Essen 4760 67
Glasgow 3731 68
Dusseldorf 3737 63
Wilno 1620 28
Helsinki 3597 56
Malaga 3757 57
Brema 2948 44
Sheffield 2324 36
Hanower 3532 53
Lipsk 1871 29
Kopenhaga 3765 60
Drezno 1900 26
Dublin 1986 31
Norymberga 4178 69
Duisburg 3948 61
oraz:
Essen 4760
Wilno 1620
Podpunkt 3

Tutaj przyda nam się klasa/struktura lokalu utworzona w poprzednim podpunkcie. Stworzymy również obiekt miasta, a w nim funkcję, która doda unikalny lokal do listy. Dzięki temu wszystkie dane będą odpowiednio uporządkowane, a my będziemy mieli do nich łatwy wgląd. Następnie standardowo iterujemy poprzez plik, tworząc obiekty miast, a w nich listę obiektów lokali, która zawiera jedynie te o unikalnym polu. Iterując jednocześnie sprawdzimy, czy ilość unikalnych lokali w danym mieście jest najmniejsza/największa spośród wszystkich.
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 |
#include <iostream> #include <fstream> #include <vector> //wymagany import!! using namespace std; struct Room{ //tworzymy strukture pomocnicza, przechowujaca dane o pomieszczeniach int x = -1; int y = -1; }; struct City{ //stworzymy strukture pomocnicza, ktora przechowa inforamcje o miastach string name = ""; //nazwa miasta vector<Room> rooms; //unikalne pomieszczenia void addRoom(int x, int y){ //funkcja dodajaca pomieszczenie tylko wtedy, gdy nie ma pomiezczenia o takim polu w vectorze for (const auto& element : rooms){ if(element.x * element.y == x * y){ return; } } Room r; r.x = x; r.y = y; rooms.push_back(r); } }; bool isNumber(string s){ //funckja pomocnicza, sprawdzajaca czy dany tekst jest liczba for(char c : s){ //jezeli chociaz jeden znak w tekscie nie bedzie cyfra if(!isdigit(c)){ return false; //to oznacza ze tekst nie jest liczba } } return true; //w przecwinym wypadku tekst jest liczba } int main() { fstream file; ofstream solution("C:\\wynik_4_3.txt"); //otwieramy plik wyjsciowy file.open("galerie.txt", ios_base::in); //otwieramy plik zrodlowy if(!file || !solution){ //jezeli nie uda sie otworzyc ktoregokolwiek z pliku, zwroc blad perror("Nie udalo sie wczytac plikow"); return 1; } string s, maxAreaCity, minAreaCity; //tworzymy zmienne pomocnicze dla max i min miasta City city, maxCity, minCity; bool isCity = false; //zmienna pomocnicza int x = -1; int y = -1; unsigned int maxDifferentRooms = 0; //zmienna przechowujaca max ilosc roznych pomieszczen unsigned int minDifferentRooms = INT_MAX; //zmienna przechowujaca min ilosc roznych pomieszczen while(file >> s){ //zczytujemy wszystkie wyrazy do zmiennej s if(s == "0"){//jezeli natrafimy na 0, - czyli koniec pomieszczen, kontynuujemy continue; } else if(!isNumber(s)){ //jezeli wyraz nie jest liczba if(!isCity){ //jezeli nie jest miastem, to pomijamy go i przelaczamy zmienna pomocznicza - nastepny wyraz bedzie nazwa miasta isCity = true; continue; } else {//jezeli natrafilismy na miasto if(city.name != ""){ //sprawdzamy, czy poprzednie miasto (o ile bylo znalezione) nie spelnia wymagan zadania: if(city.rooms.size() > maxDifferentRooms){ maxDifferentRooms = city.rooms.size(); maxCity = city; } if(city.rooms.size() < minDifferentRooms){ minDifferentRooms = city.rooms.size(); minCity = city; } } city = City(); //nastepnei resetujemy wartosci city.name = s; isCity = false; } }else{ if(x == -1){ //jezeli nie mamy jeszcze pierwszego wymiaru x = stoi(s); //ustawiamy go }else { y = stoi(s); city.addRoom(x, y); //w przeciwnym wypadku probujemy dodac unikalne pomieszczenie x = -1; y = -1; } } } if(city.name != ""){ //musimy jeszcze sprawdzic ostatnie miasto if(city.rooms.size() > maxDifferentRooms){ maxDifferentRooms = city.rooms.size(); maxCity = city; } if(city.rooms.size() < minDifferentRooms){ minDifferentRooms = city.rooms.size(); minCity = city; } } solution << maxCity.name << " " << maxCity.rooms.size() << endl; //na koniec zapisujemy wyniki do pliku solution << minCity.name << " " << minCity.rooms.size() << endl; solution.close(); //zamykamy pliki file.close(); system("pause"); return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 |
package matura; import java.io.BufferedReader; import java.io.BufferedWriter; import java.io.File; import java.io.FileReader; import java.io.FileWriter; import java.util.ArrayList; class City{ //tworzymy pomocnicza, lokalna klase miasta private ArrayList<Integer> uniqueRooms; //lista przechowujaca unikalne pomieszczenia private String name; //nazwa miasta public City(String Name) { //konstruktor przyjmujacy nazwe miasta jako argument name = Name; uniqueRooms = new ArrayList<Integer>(); } public void addRoom(int x, int y) { //funckja dodajaca unikalne pomieszczenia if(uniqueRooms.contains(x*y)) //jezeli pomieszczenie o takim polu zostalo juz dodane { return; //wyjdz z funkcji } uniqueRooms.add(x*y); // w przeciwnym wypadku dodaj unikalne pomieszczenie do listy } public int getCount() { //funkcja pomocnicza dajaca dostep do prywatnego pola - ilosc unikalnych pomieszczen return uniqueRooms.size(); } public String getName() { //funkcja pomocnicza dajaca dostep do prywatnego pola - nazwa miasta return name; } } public class Zad3 { public static void main(String[] args) { try { //otaczamy kod w try/catch - dzieki temu wszelkie bledy z plikami zostana zraportowane File f = new File("C://galerie.txt"); //wskazujemy sciezke pliku zrodlowego BufferedReader br = new BufferedReader(new FileReader(f)); //otwieramy plik przy uzyciu BufferedReader i FileReader, aby moc z niego czytac File f2 = new File("C://java/wynik4_3.txt"); //wskazujemy sciezke pliku wyjsciowego if(!f2.exists()) { f2.createNewFile(); //tworzymy plik a, jeżeli nie istnieje } BufferedWriter wr = new BufferedWriter(new FileWriter(f2)); //otwieramy plik a przy uzyciu BufferedWriter i FileWrited, aby moc do niego zapisywac String line; //zmienna pomocnicza przechowujaca aktualny wiersz City maxCity = new City(""); //zmienna pomocnicza przechowujaca miasto z galeria o najwiekszej ilosci pomieszczen roznych typow City minCity = new City(""); //zmienna pomocnicza przechowujaca miasto z galeria o najmniejszej ilosci pomieszczen roznych typow City city = new City(""); //zmienna pomocnicza przechowujaca aktualne miasto while((line = br.readLine()) != null) { //dopoki nie napotkamy konca pliku if(city.getCount() > 0) { //jezeli mamy juz jakas galerii if(city.getCount() > maxCity.getCount()) { //jezeli ilosc unikalnych pomieszczen jest wieksza od maksymalnej maxCity = city; //zapisujemy jej dane } else if(city.getCount() < minCity.getCount()) { //jezeli ilosc unikalnych pomieszczen jest wieksza od maksymalnej minCity = city; //zapisujemy jej dane } else if(minCity.getCount() == 0) { //jezeli nie znalezlismy jeszcze zadnej galerii o najmniejszej ilosci roznych pomieszczen minCity = city; //zapisujemy dane aktualnej galerii } } String[] splitted = line.split(" "); //dzielimy wiersz spacjami city = new City(splitted[1]); //pobieramy nazwe miasta - drugi wyraz int x = -1; //ustawiamy zmienna pomocnicza przechowujaca pierwszy wymiar pomieszczenia - wartosc ujemna oznacza, ze jeszcze takiej nie znalezlismy for(int i=2; i < splitted.length; i++) { //petla wewnetrzna iterujaca poprzez wszystkie liczby w wierszu if(x == -1) { //jezeli jeszcze nie mamy pierwszego wymiaru x = Integer.parseInt(splitted[i]); //zapisujemy go if(x == 0) //jezeli napotkalismy 0 - koniec pomieszczen { break; //przerywamy dzialanie wewnetrznej petli } } else { //jezeli mamy juz x city.addRoom(x, Integer.parseInt(splitted[i])); x = -1; //resetujemy pierwszy wymiar } } } if(city.getCount() > 0) { //musimy sprawdzic tez ostatnia galerie if(city.getCount() > maxCity.getCount()) { //jezeli ilosc unikalnych pomieszczen jest wieksza od maksymalnej maxCity = city; //zapisujemy jej dane } else if(city.getCount() < minCity.getCount()) { //jezeli ilosc unikalnych pomieszczen jest wieksza od maksymalnej minCity = city; //zapisujemy jej dane } } br.close(); //po zakonczonej pracy z plikiem nalezy go zamknac wr.write(maxCity.getName() + " " + maxCity.getCount() + " \n"); wr.write(minCity.getName() + " " + minCity.getCount() + " \n"); wr.close(); //po zakonczonej pracy z plikiem a nalezy go zamknac } catch (Exception e) { e.printStackTrace(); } } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
class City: #tworzymy pomocnicza klase miasta uniqueRooms = [] #zmieanna przechowujaca pola unikalnych pomieszczen name = "" #nazwa miasta def __init__(self, Name): #konstruktor klasy self.uniqueRooms = [] #inicjalizujacy zmienne self.name = Name def addRoom(self, x1, y1): #funkcja dodajaca pomieszczenie tylko wtedy, gdy jest ono unikalne w danym miescie val = x1 * y1 if not self.uniqueRooms.__contains__(val): self.uniqueRooms.append(val) def getCount(self): #funkcja zwracajaca ilosc unikalnych pomieszczen return len(self.uniqueRooms) inputFile = open("C:\\galerie.txt", "r") #otwieramy plik zrodlowy w trybie read outputFile = open("C:\\python\\wynik4_3.txt", "w") #otwieramy plik wyjsciowy w trybie write maxCity = City("") #zmienna przechowujaca nazwe miasta o najwiekszej ilosci roznych pomieszczen minCity = City("") #zmienna przechowujaca nazwe miasta o najmniejszej ilosci roznych pomieszczen city = City("") for line in inputFile: #iterujemy poprzez kazdy wiersz w pliku zrodlowym splitted = line.split(" ") #dzielimy wiersz na pojedyncze wyrazy city = City(splitted[1]) #tworzymy isntancje naszej klasy pomocniczej x = -1 #stawiamy zmienna pomocnicza przechowujaca pierwszy wymiar pomieszczenia - wartosc ujemna oznacza, ze jeszcze takiej nie znalezlismy for i in range(2, len(splitted)): #iterujemy poprzez wszystkie wymiary w wierszu if x == -1: #jezeli nie mamy jeszcze pierwszego wymiaru x = int(splitted[i]) #zapisujemy go if x == 0: #jezeli napotkamy 0 break #przerywamy dzialanie wewnetrznej petli else: #w przeciwnym wypadku city.addRoom(x, int(splitted[i])) #dodajemy pomieszczenie do miasta x = -1 #resetujemy pierwszy wymiar if maxCity.getCount() < city.getCount(): #jezeli galeria miala wieksza ilosc roznych pomieszczen niz ta najwieksza maxCity = city #zapisujemy jej dane if minCity.getCount() > city.getCount(): #jezeli galeria miala mniejsza ilosc roznych pomieszczen niz ta najmniejsza minCity = city #zapisujemy jej dane if minCity.getCount() == 0: #jezeli nie znalezlismy jeszcze galerii o najmniejszej powierzchni minCity = city #zapisujemy aktualna outputFile.write(maxCity.name + " " + str(maxCity.getCount()) + "\n") #na koniec zapisujemy do pliku nazwy miast outputFile.write(minCity.name + " " + str(minCity.getCount()) + "\n") #o najwiekszych i najmniejszych ilosciach unikalnych pomieszczen inputFile.close() #zamykamy plik zrodlowy outputFile.close() #zamykamy plik wyjsciowy |
Powyższe programy drukują następujący wynik:
Berlin 35
Kolonia 18

Próbna matura z informatyki 2021 zadanie 5 – telefony

W zadaniu tym mamy uporządkowany zbiór informacji o telefonach wykonywanych przez daną firmę. Jak pewnie się domyślacie użyjemy tutaj Excela – podobnie jak w maju, próbna matura z informatyki wymaga użycia tego programu. Poniżej pokazałem jak importować dane:
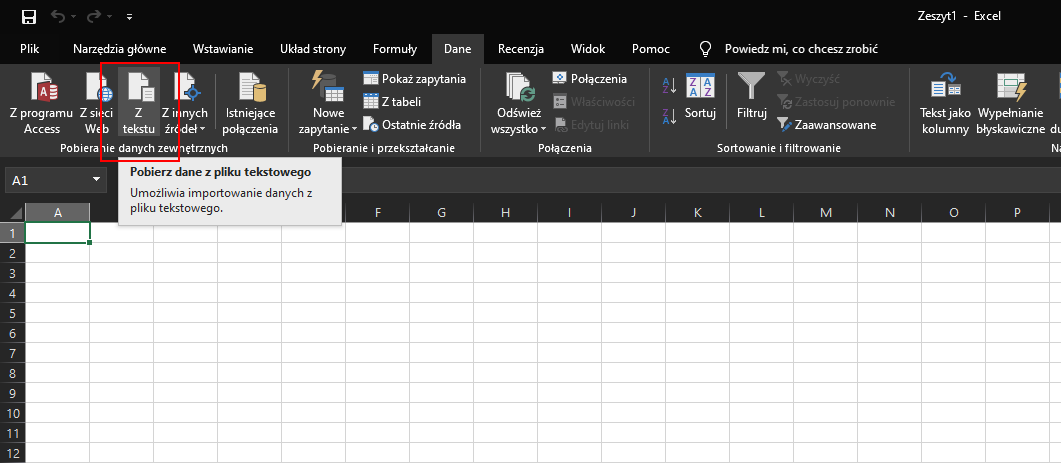
Z zakładki Dane wybieramy Z tekstu, a następnie wybieramy plik z danymi.
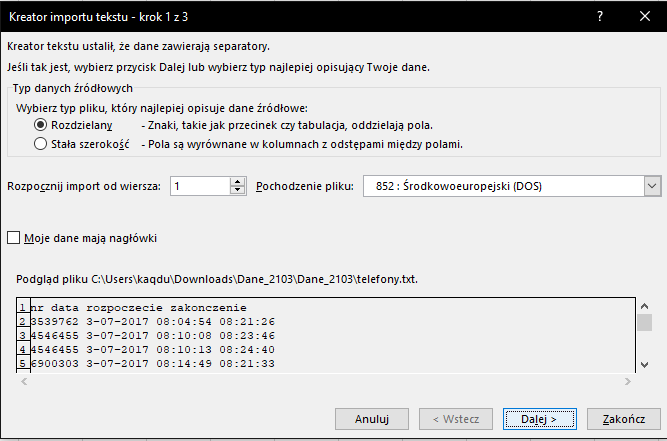
W okienku, które wyskoczyło kliknij Dalej
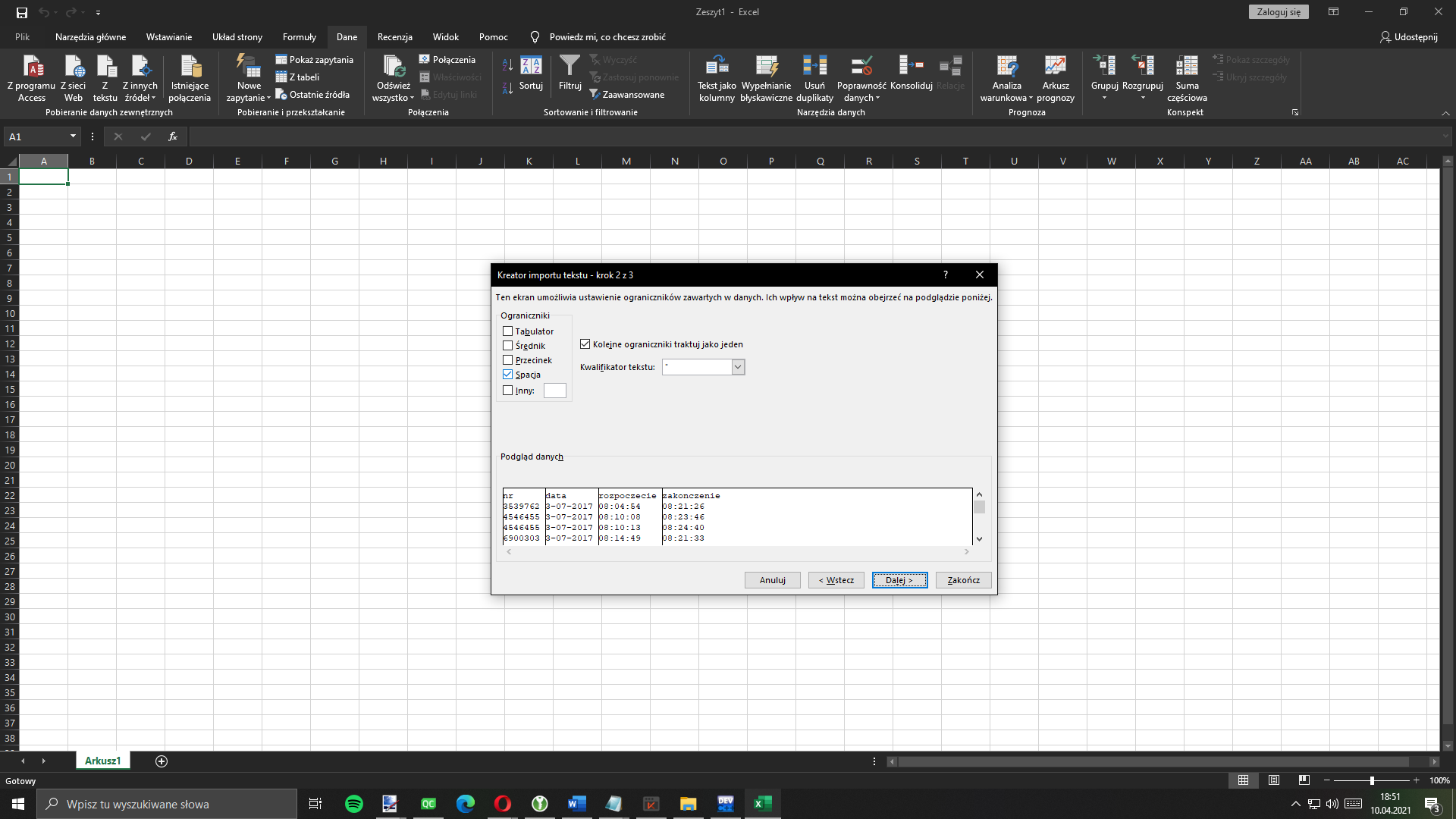
Następnie z ograniczników wybierz Spację i kliknij Dalej. W następnych okienkach nic nie zmieniaj i kliknij Zakończ.
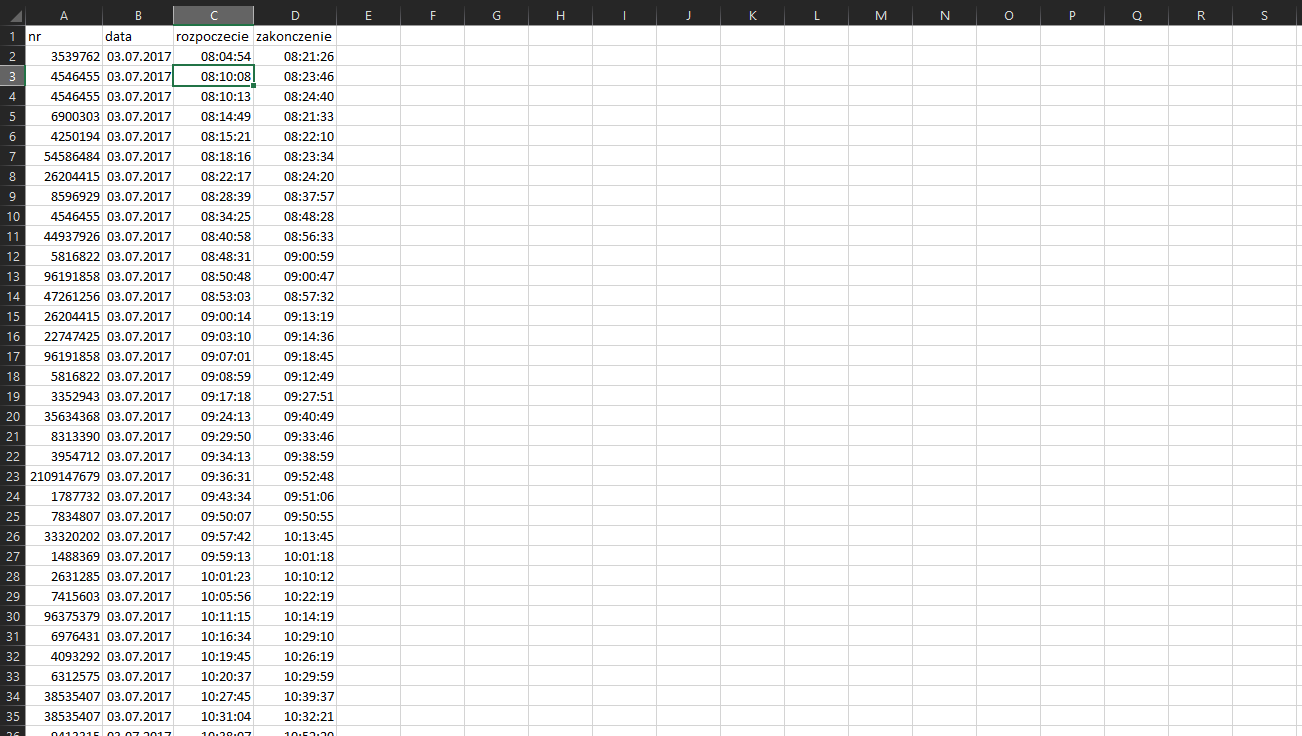
Mając zaimportowane dane możemy przystąpić do rozwiązywania podpunktów.
Podpunkt 1

Do wykonania tego podpunktu skorzystamy ze sumy częściowej. W tym celu przy użyciu skrótu Ctrl+A zaznaczymy wszystkie dane, a następnie posortujemy je według numeru telefonu:
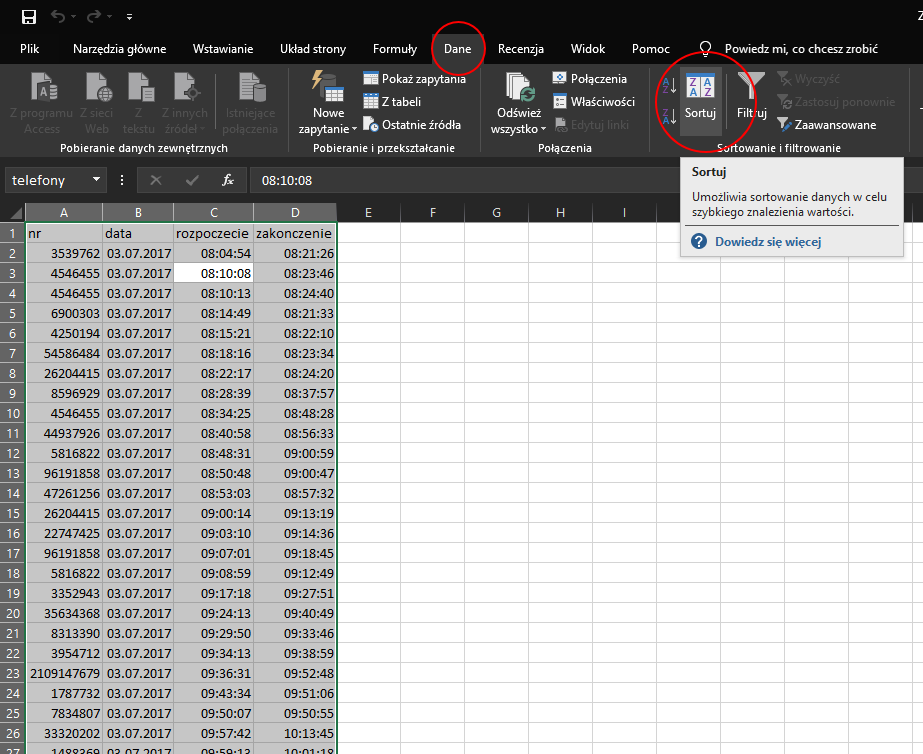
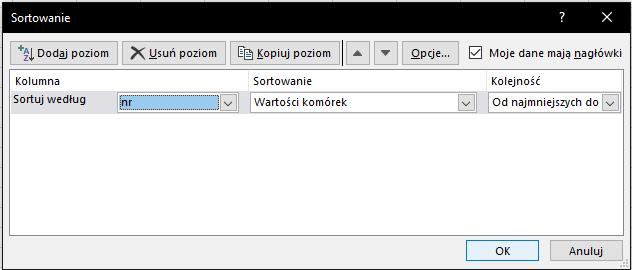
Następnie z grupy Konspekt wybieramy Suma częściowa i uzupełniamy tak, jak na zdjęciu poniżej:
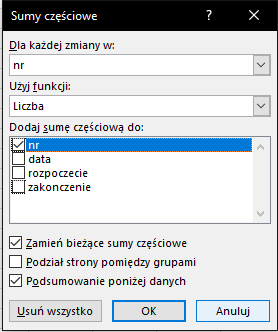
Następnie z grupy Konspekt wybierz Ukryj szczegóły. Mamy już ilość połączeń dla każdego numeru. Teraz wystarczy znaleźć 3 największe. W tym celu zaznacz w całości kolumny zawierające numer i ilość połączeń. Z zakładki Narzędzia główne z menu Znajdź i zaznacz wybierz Przejdź do – specjalne… i wybierz Tylko widoczne komórki. Dzięki temu skopiujesz sam wynik działania sumy częściowej, a następnie będziesz mógł go wkleić w oddzielnym arkuszu i posortować:
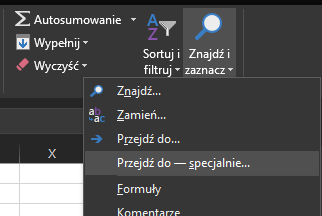
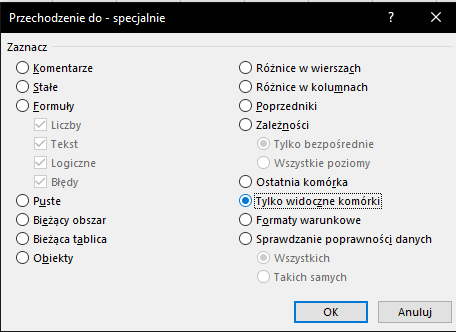
Skopiuj zaznaczone kolumny i wklej w nowym arkuszu. Następnie zaznacz wszystko i zakładki dane wybierz Sortuj:
Wybieramy sortowanie od największych do najmniejszych. Oto rozwiązanie:
Podpunkt 2

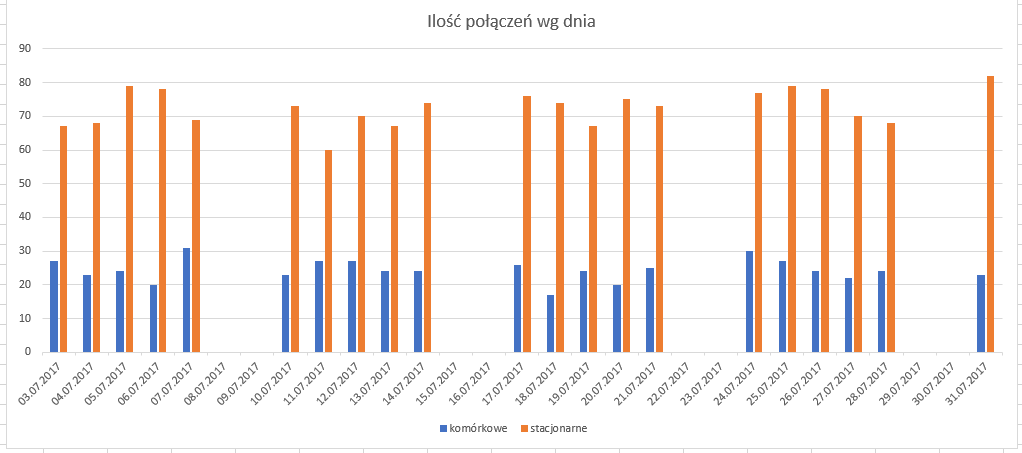
Aby wykonać ten podpunkt do naszych danych dodamy dwie kolumny: pierwsza, która będzie informowała o tym, czy numer jest stacjonarny, a druga o tym, czy jest komórkowy. Następnie posortujemy dane najpierw według stacjonarnych, skopiujemy dane do oddzielnego arkusza i ponownie skorzystamy ze sumy częściowej. To samo wykonamy dla numerów komórkowych. Następnie połączone wyniki obu sum częściowych zestawimy w oddzielnej tabeli i na jej podstawie utworzymy wykres. Oto jak to zrobić:
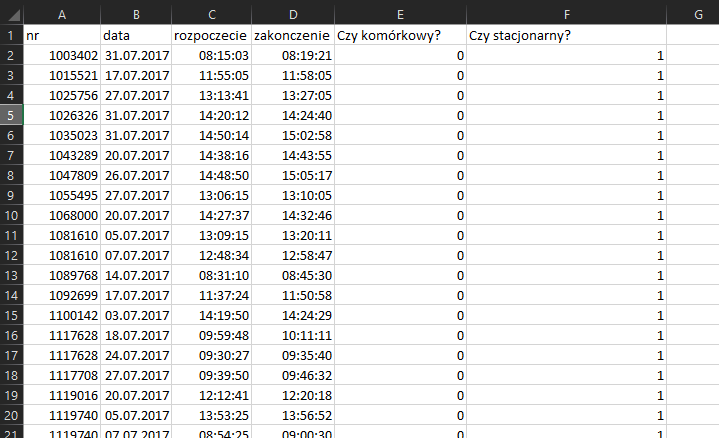
Utworzyliśmy dwie nowe kolumny. Kolumna sprawdzająca, czy jest to numer komórkowy ma formułę ogólną =JEŻELI(DŁ(A2)=8;1;0) – jeżeli długość numeru jest równa 8 zwróci jeden, w przeciwnym wypadku 0. Analogiczną formułę zastosowaliśmy w kolumnie obok, z tym że tam sprawdzamy czy długość jest równa 7.
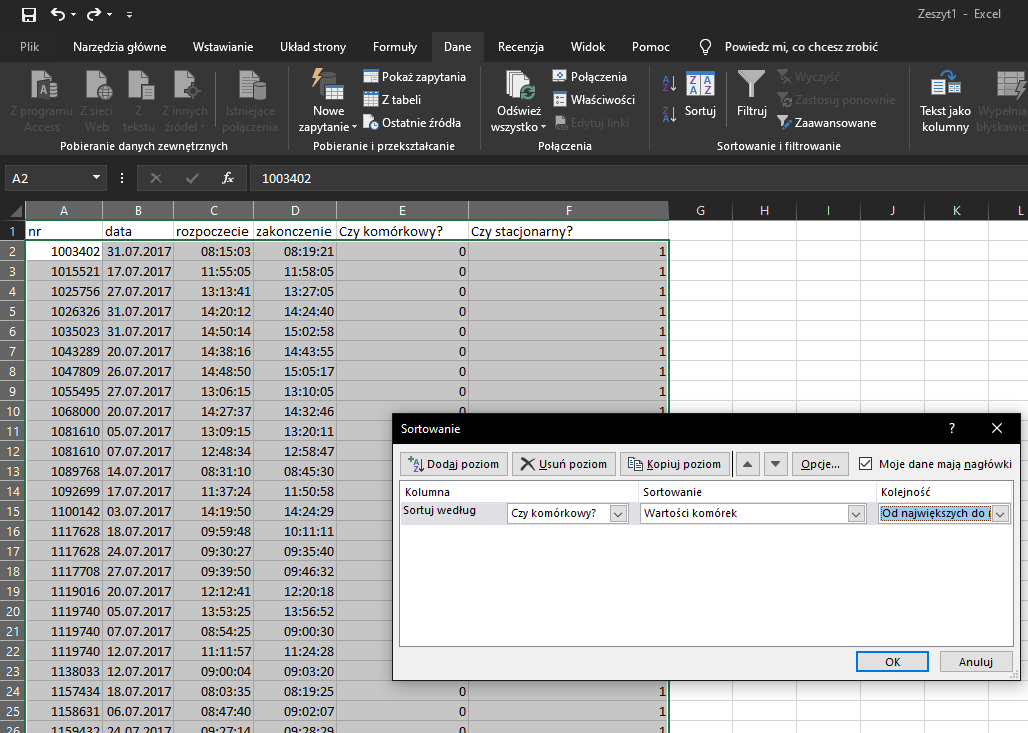
Następnie sortujemy dane według numerów komórkowych. Następnie posortowane dane, dla których kolumna Czy komórkowy? Przyjmuje wartość 1 kopiujemy do nowego arkusza. Następnie wklejone dane musimy posortować według daty. Potem możemy skorzystać ze sumy częściowej:
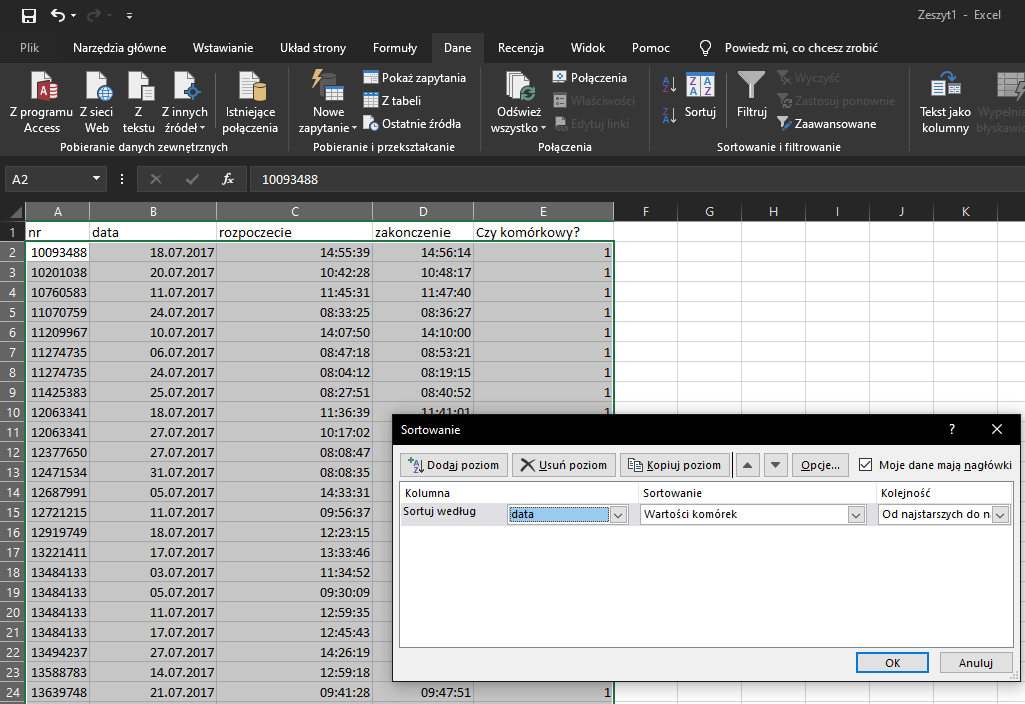
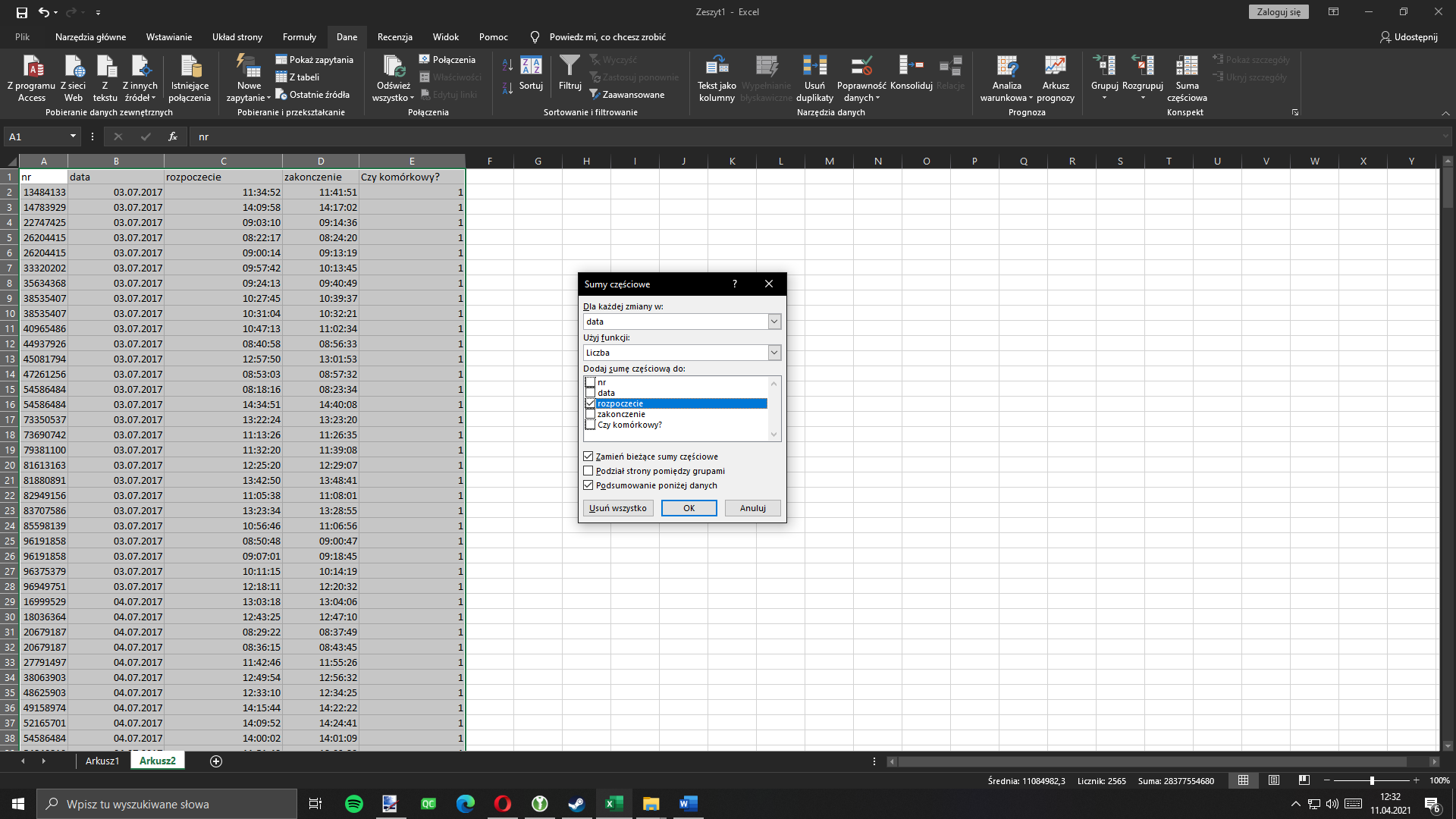
Następnie, tak jak w pierwszym podpunkcie, ukrywamy szczegóły i kopiujemy tylko widoczne komórki do oddzielnego arkusza:
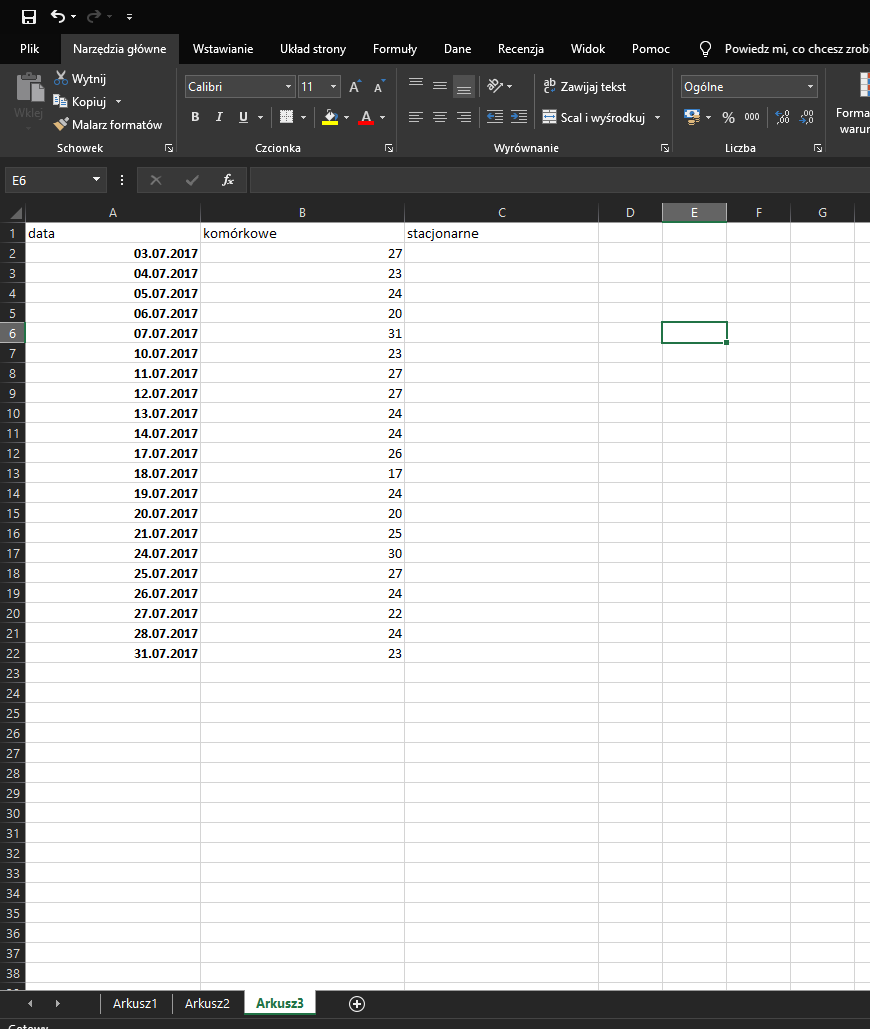
Powyższe kroki powtarzamy dla numerów stacjonarnych, wklejając wynik sumy częściowej do tego samego arkusza, co wynik sumy częściowej dla komórkowych:
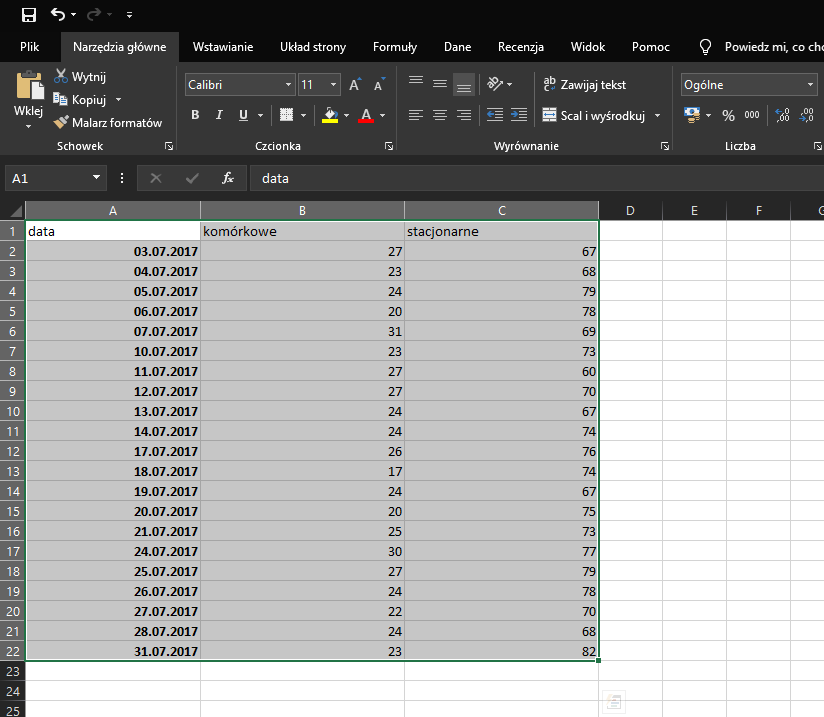
Następnie pozostaje nam już tylko wykonać wykres na podstawie danych, które mamy. Pamiętajcie o odpowiednim zatytułowaniu wykresu!
Podpunkt 3

W tym podpunkcie stworzymy oddzielną kolumnę, która sprawdzi warunek z zadania. Następnie skorzystamy z formuły SUMA oraz SUMA.JEŻELI, a także odpowiedniej funkcji matematycznej, aby zaokrąglić wynik:
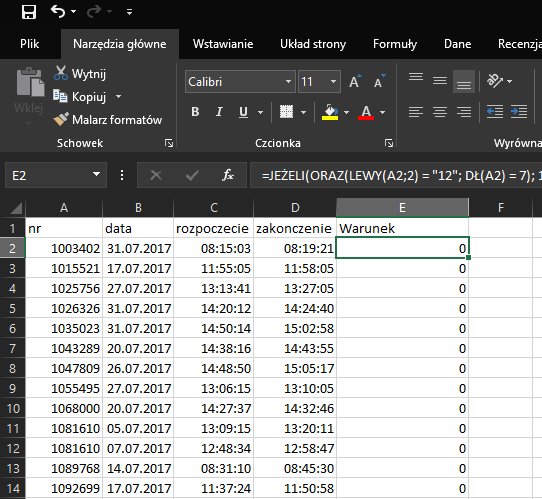
Formuła =JEŻELI(ORAZ(LEWY(A2;2) = „12”; DŁ(A2) = 7); 1; 0) sprawdza, czy pierwsze dwa znaki w komórce są równe 12, a także czy numer jest stacjonarny.Jeżeli tak, to zwróci jeden, w przeciwnym wypadku zero.
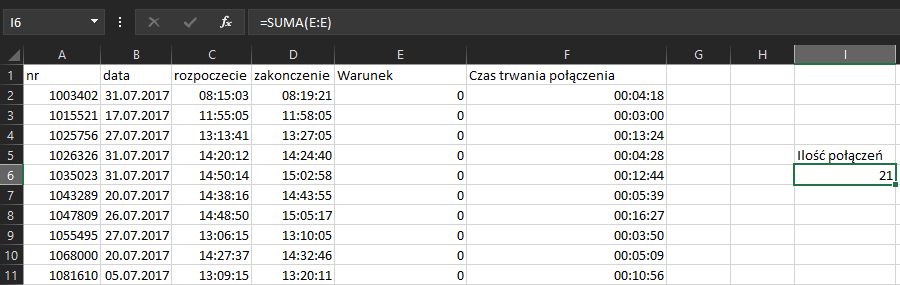
Aby obliczyć łączną ilość połączeń wystarczy teraz tylko zsumować wszystkie wartości warunku z kolumny.
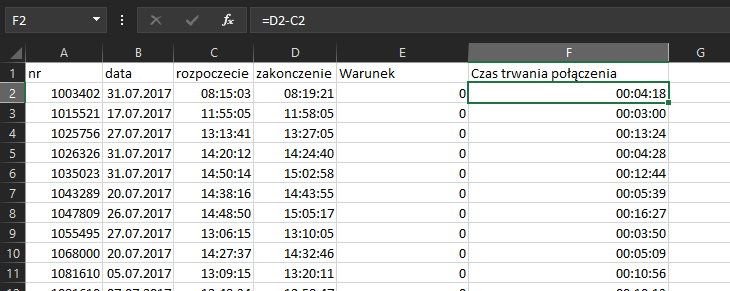
Tworzymy kolejną kolumnę, która obliczy nam czas trwania danego połączenia o formule =D2-C2.
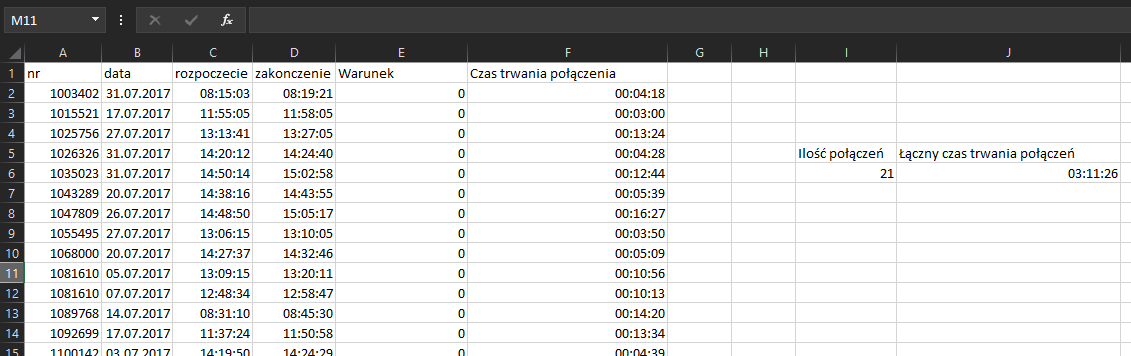
Łączny czas połączeń obliczymy korzystając z formuły =SUMA.JEŻELI(E:E;”=1″;F:F), która zliczy wszystkie wartości z kolumny F dla wierszy spełniających podany warunek w kolumnie E. Musimy jeszcze tylko zaokrąglić łączny czas do pełnych minut w górę:
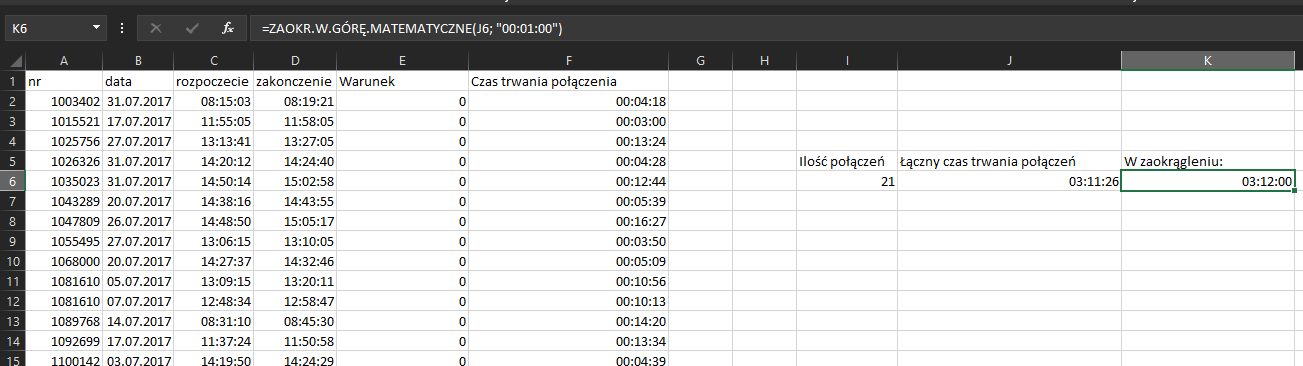
Korzystamy z formuły =ZAOKR.W.GÓRĘ.MATEMATYCZNE(J6; „00:01:00”) i otrzymujemy wynik: 21 połączeń trwających łącznie w zaokrągleniu do pełnych minut 3h i 12min lub 192 min.
Podpunkt 4

W podpunkcie tym ponownie stworzymy kolumnę, która policzy czas trwania połączenia w minutach. Następnie utworzymy kolumnę, która zwróci typ numeru telefonu dla danego połączenia. W kolejnych kolumnach zawrzemy informacje o pakietach rozmów – zarówno z abonamentu, jak i dla komórkowych, stacjonarnych i zagranicznych.
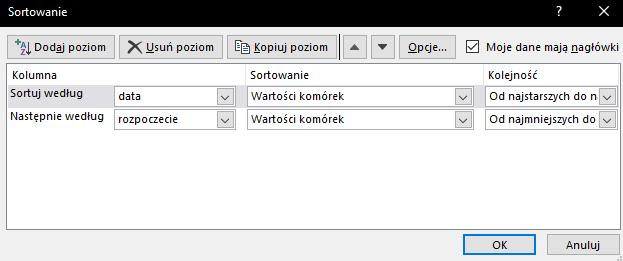
Najpierw posortujmy dane chronologicznie – najpierw wg daty, a następnie wg godziny rozpoczęcia.
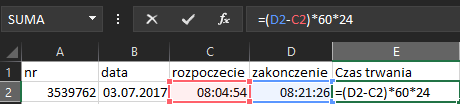
Kolejnym krokiem jest obliczenie czasu trwania połączenia. Mnożymy wynik razy 1440, aby otrzymać czas połączenia w minutach.

Następnie sprawdzamy typ telefonu – 0 dla stacjonarnego, 1 dla komórkowego, 2 dla zagranicznego, a 3 dajemy w razie, gdyby CKE zrobiło nam niespodziankę i dodało numer spoza kryteriów 😀
Formuła: =JEŻELI(DŁ(A2)=7;0;JEŻELI(DŁ(A2)=8;1;JEŻELI(DŁ(A2>=10);2;3)))

Następnie tworzymy kolumnę, która będzie obliczała ile pakietu rozmów z abonamentu zostało. Zaczynamy od wartości 800 pomniejszoną o czas trwania pierwszej rozmowy.

W kolejnych wierszach zmniejszamy wartość abonamentu o czas trwania rozmowy, jeżeli jest to rozmowa z telefonem komórkowym/stacjonarnym. Jeżeli limit został już wyczerpany, to komórka przyjmie po prostu wartość 0.
Formuła: =JEŻELI(G3>0; JEŻELI(LUB(F4=0;F4=1); G3-E4; G3);0)

Kolejnym krokiem jest stworzenie kolumn obliczających pakiet minut dla danego typu telefonu. Najpierw trzeba oczywiście sprawdzić, czy połączenie jest z danego typu. Następnie sprawdzamy, czy pakiet komórkowy/stacjonarny został już wykorzystany. Jeżeli tak, to trzeba sprawdzić, czy jego wartość jest mniejsza od zera. Jeżeli tak, to trzeba tą wartość również odjąć od pakietu, który właśnie się zaczyna. Następnie pakiet ten należy również pomniejszyć o ilość minut z aktualnego połączenia. Jeżeli w poprzedniej rozmowie pakiet został wykorzystany, trzeba go odnowić, dodając 100 minut.
Formuła dla połączeń stacjonarnych: =JEŻELI(F3=0;JEŻELI(G3>0;H2; JEŻELI(G3<0; H2+G3;JEŻELI(H2<=0; 100-E3+H2; H2-E3)));JEŻELI(H2 < 0; 100+H2; H2))

Formuła dla połączeń komórkowych jest analogiczna – zmienia się jedynie sprawdzany typ telefonu i odpowiednie komórki: =JEŻELI(F3=1;JEŻELI(G3>0;I2; JEŻELI(G3<0; I2+G3;JEŻELI(I2<=0; 100-E3+I2; I2-E3)));JEŻELI(I2 <= 0; 100+I2; I2))

W kolejnej kolumnie obliczamy koszt połączenia, jeżeli jest ono zagraniczne. Liczy się każda zaczęta minuta, więc wystarczy zaokrąglić ilość minut w górę.
Formuła: =JEŻELI(F2=2; ZAOKR.W.GÓRĘ.MATEMATYCZNE(E2); 0)
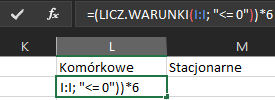
Możemy przejść do zliczania kosztów. Sprawdzamy ile razy pakiet minut komórkowych osiągnął wartość ujemną – czyli ile razy został wykorzystany. Daną wartość mnożymy przez koszt za minutę.
Formuła: =(LICZ.WARUNKI(I:I; „<= 0”))*6
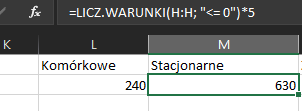
Formuła jest analogiczna dla połączeń stacjonarnych – zmienia się jedynie sprawdzana kolumna oraz koszt za minutę: =LICZ.WARUNKI(H:H; „<= 0”)*5
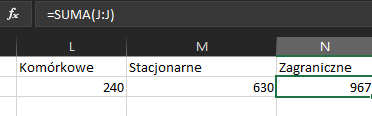
Dla połączeń zagranicznych wystarczy tylko zsumować obliczone wcześniej koszty połączeń: =SUMA(J:J)

Na koniec trzeba jeszcze pamiętać o koszcie abonamentu. Możemy już zliczyć wszystkie koszty otrzymując wynik 1867.
Próbna matura z informatyki 2021 zadanie 6 – wyścigi


W ostatnim zadaniu mamy kilka powiązanych ze sobą zbiorów informacji. Od razu nasuwa nam się więc Microsoft Access – próbna matura z informatyki nie mogłaby się obejść bez tego zadania. Przy imporcie trzeba jednak uważać na odpowiednie typu danych, a także na relacje. Przedstawimy go najpierw krok po kroku:
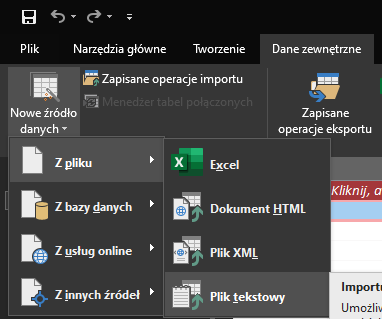
Z zakładki Dane zewnętrzne wybierz Nowe źródło danych > Plik tekstowy, a następnie wybieramy plik tabeli, który chcemy zaimportować.
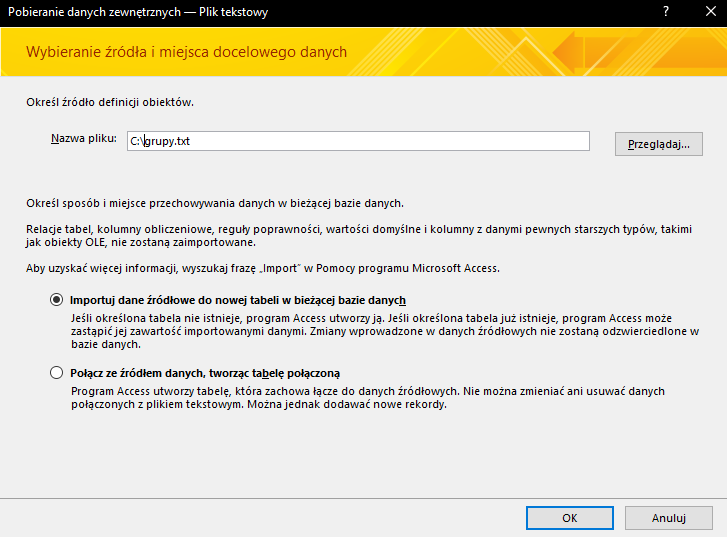
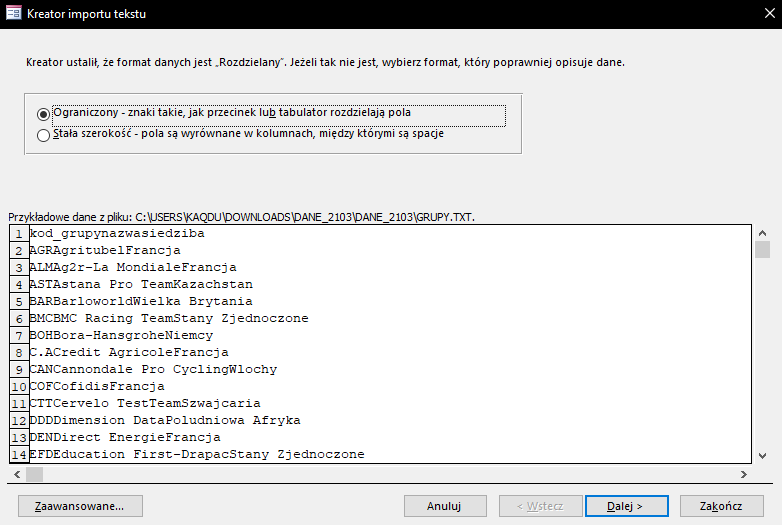
W następnym okienku klikamy dalej.
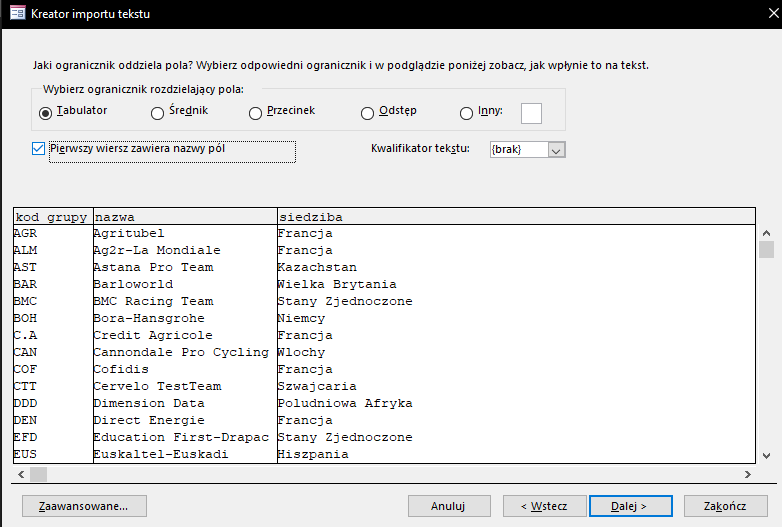
W kolejnym zaznaczamy Pierwszy wiersz zawiera nazwy pól.
W następnych oknach musimy wybrać typy pól oraz klucze podstawowe/obce. Wszystko zostało opisane poniżej:
- Dla tabeli grupy ustaw indeksowanie bez duplikatów na kolumnie kod_grupy, a w następnym oknie wybierz ją jako klucz podstawowy.
- Dla tabeli zawodnicy ustaw indeksowanie bez duplikatów na kolumnie id_zawodnika, a typ kolumny data ustaw na data i godzina. UWAGA:aby zapobiec błędom importu musisz jeszcze wejść w Zaawansowane, a następnie zmienić format daty na RMD, a także ogranicznik daty na myślnik
- Dla tabeli startujacy ustaw indeksowanie bez duplikatów na kolumnie id_startu, a także indeksowanie z duplikatami na kolumnach id_zawodnika, oraz kod_grupy. Klucz podstawowy ustaw na kolumnie id_startu.
- Dla tabeli czasy ustaw indeksowanie bez duplikatów na kolumnie id_startu. Kolumnę tą wybierz również jako klucz podstawowy.
Mając już tabele możemy je połączyć relacjami wchodząc w Narzędzia bazy danych > Relacje. Po połączeniu powinny one wyglądać tak:
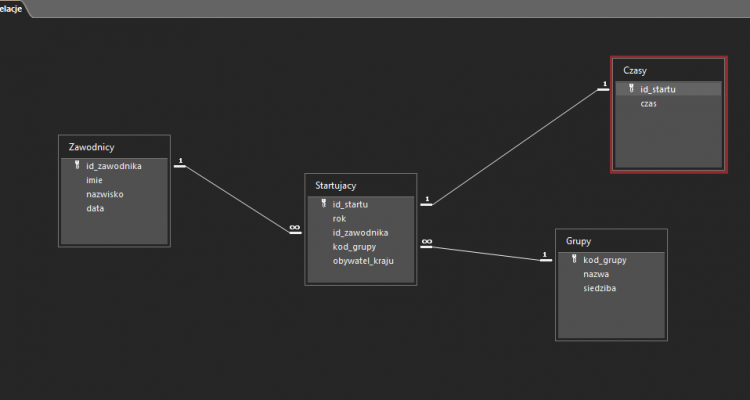
I to by było na tyle – możemy zacząć rozwiązywać zadanie.
Podpunkt 1

Dosyć prosta kwerenda niewymagająca od nas większego wysiłku. Nic dziwnego, że tylko jeden punkt, ale to zawsze dodatkowe 2% do naszego końcowego wyniku 😀
W zapytaniu tym posortujemy czasy rosnąco, a następnie ograniczymy ilość wyników do jednego. W ten sposób otrzymamy tylko jeden, najlepszy wynik spośród wszystkich:
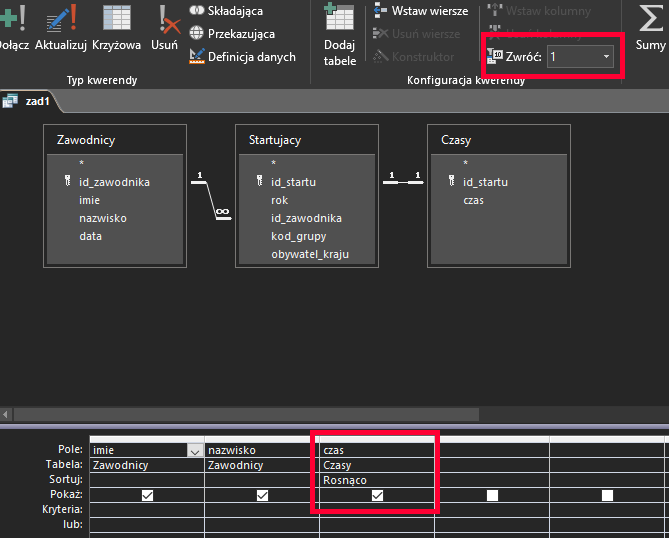
Oto wynik:

Podpunkt 2

Nieco bardziej złożony podpunkt, ale nadal nie wymaga on od nas użycia dodatkowych, pomocniczych kwerend. Wystarczy skorzystać z funkcji agregującej COUNT, a następnie posortować wyniki malejąco i ograniczyć je do jednego. Tak to się prezentuje w programie Access:
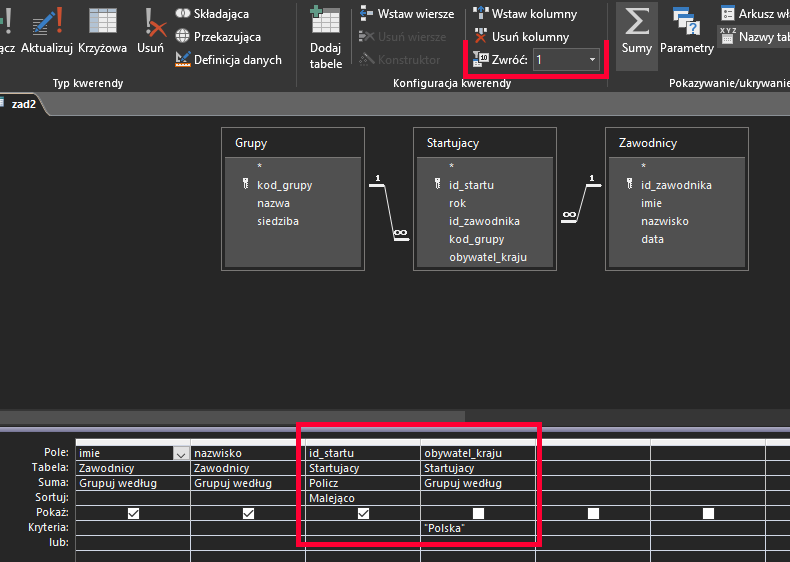
A tak wygląda wynik tego zapytania:
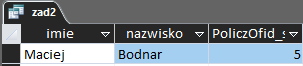
Podpunkt 3

W podpunkcie tym skorzystamy z dwóch kwerend pomocniczych. Pierwsza z nich wyznaczy wiek najmłodszego zawodnika dla każdego roku. Druga obliczy wiek dla każdego zawodnika w poszczególnych latach. Finalna kwerenda zestawi dwie powyższe, zwracając najmłodszych zawodników dla każdego roku wyścigów.
W pierwszej kwerendzie pomocniczej posługujemy się wyrażeniem, które zawiera funkcję Minimum. Zwróć uwagę, że w wyrażeniu tym obliczamy wiek dla każdego ze startujących, odejmując rok ich urodzenia (który z kolei jest zwracany dzięki funkcji Year) od aktualnego roku. Dodatkowo korzystamy też tutaj z grupowania. Domyślnie nie jest ono widoczne, więc musisz kliknąć Sumy w prawym górnym rogu zakładki Projektowanie:
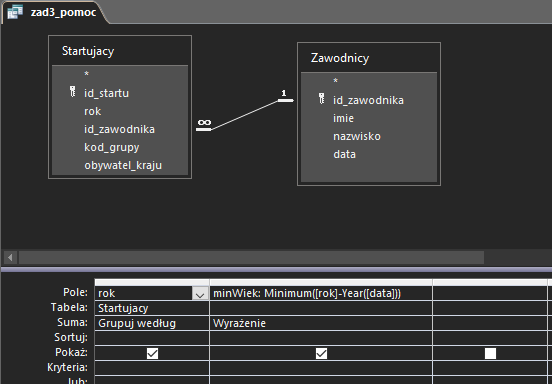
W następnej pomocniczej kwerendzie obliczamy wiek każdego z zawodników, przy pomocy prostego wyrażenia:
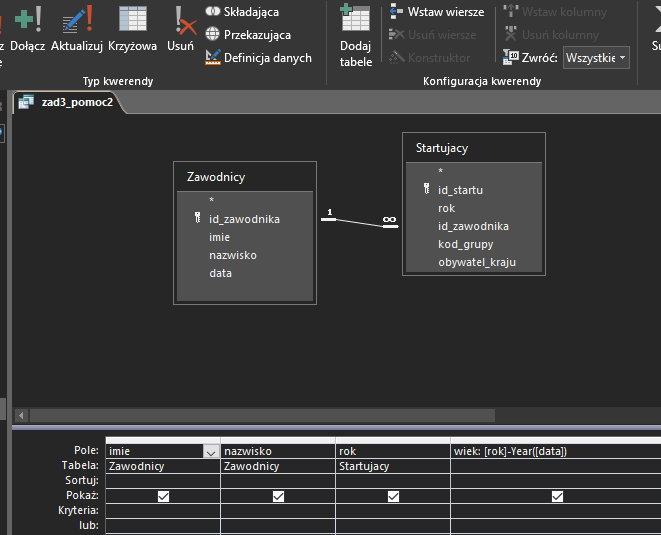
W ostatniej, finalnej kwerendzie łączymy dwie poprzednie, poprzez kryteria. Dodatkowo sortujemy dane, aby wynik był łatwiejszy do odczytania:
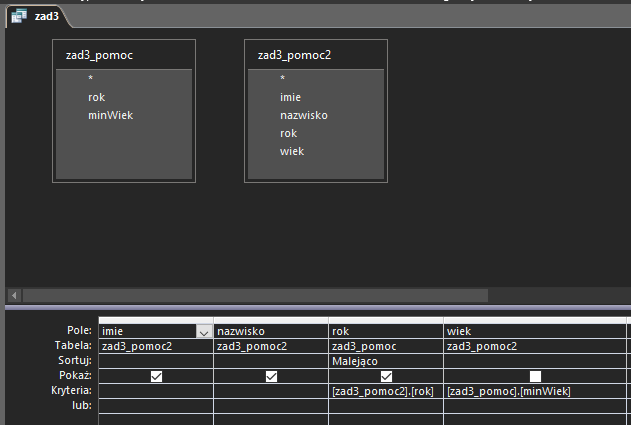
Tak wygląda odpowiedź:
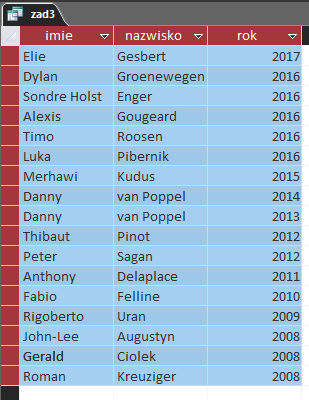
Podpunkt 4

W podpunkcie tym ponownie skorzystamy z dwóch pomocniczych kwerend. Pierwsza z nich obliczy liczbę startujących zawodników dla każdego roku. Druga za pomocą relacji LEFT JOIN obliczy ilu zawodników nie ukończyło wyścigu w danym roku. Na koniec w finalnej kwerendzie możemy wybrać rok, w którym takich zawodników było najwięcej.
Pierwsza kwerenda korzysta z funkcji agregującej COUNT. Zliczamy dzięki niej ilu zawodników wystartowało w każdym roku:
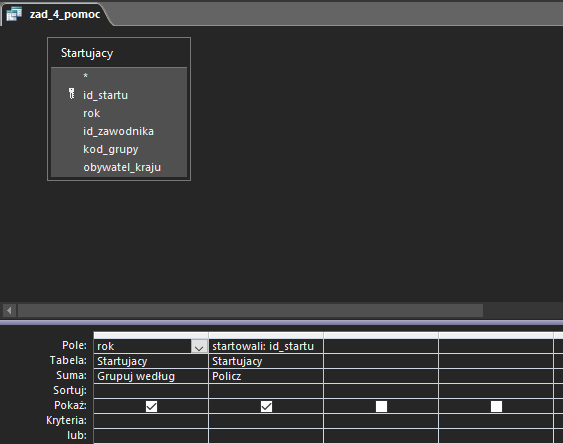
W kolejnej kwerendzie ponownie korzystamy z funkcji zliczającej:
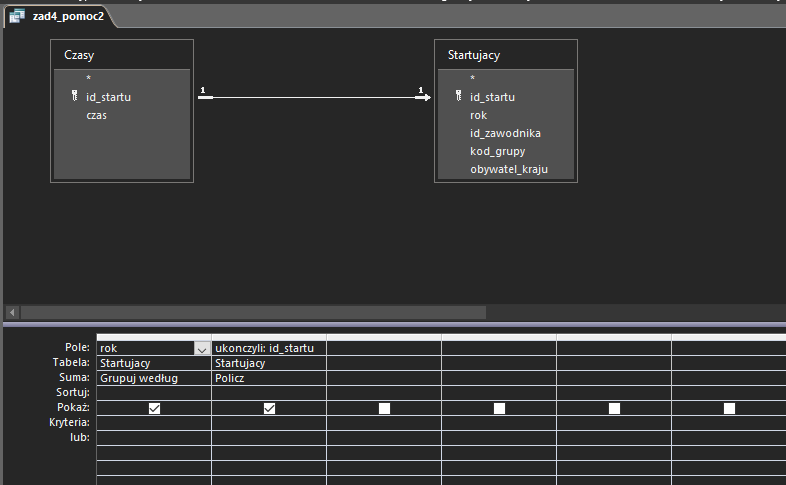
Tym razem jednak musimy zmienić typ relacji na LEFT JOIN – dzięki temu wybrane zostaną jedynie te rekordy, które nie istnieją w tabeli Czasy. Jak to zrobić? Kliknij prawym na strzałkę relacji łączącą dwie tabele, a następnie wybierz Właściwości sprzężenia i zaznacz trzecią opcję:
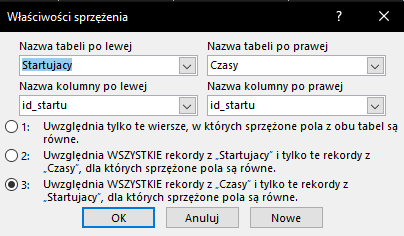
Następnie w finalnej kwerendzie możemy łączymy obie kwerendy pomocnicze poprzez kryteria, a następnie sortujemy wyniki malejąco i ograniczamy je do jednego rekordu, aby uzyskać rok o największej liczbie zawodników, którzy nie ukończyli wyścigu:
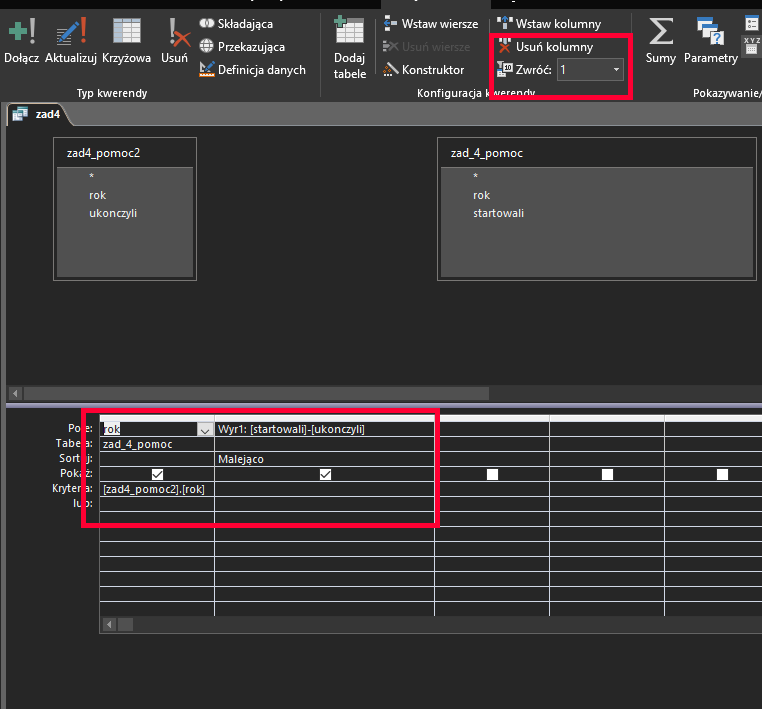
Oto wynik naszej finalnej kwerendy:
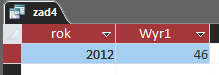
Podpunkt 5

W podpunkcie tym musimy podać dwie odpowiedzi. W tym celu ponownie skorzystamy z dwóch pomocniczych zapytań. Pierwsze z nich wybierze wszystkie unikalne narodowości dla danej grupy w każdym roku. Druga zliczy ile unikalnych narodowości wchodziło w skład jednej grupy.
Projekt pierwszej z kwerend wygląda następująco:
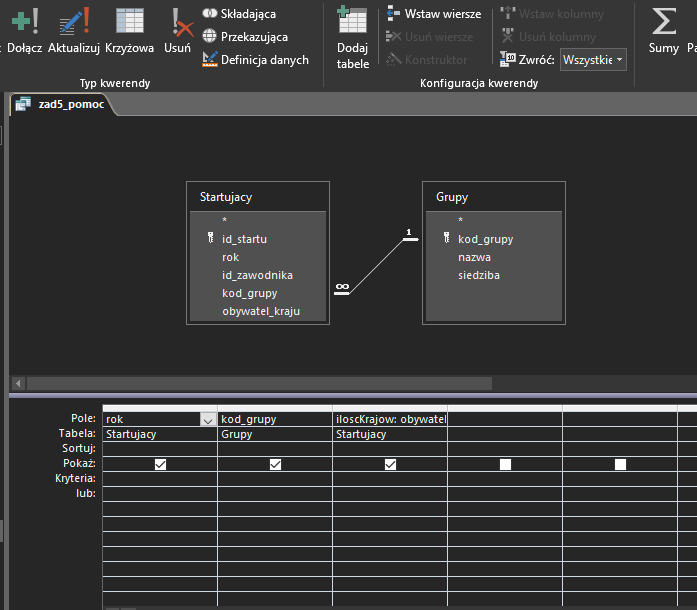
Aby jednak kraje nie powtarzały się, trzeba wejść w widok SQL i dodać słowo kluczowe DISTINCT po SELECT:
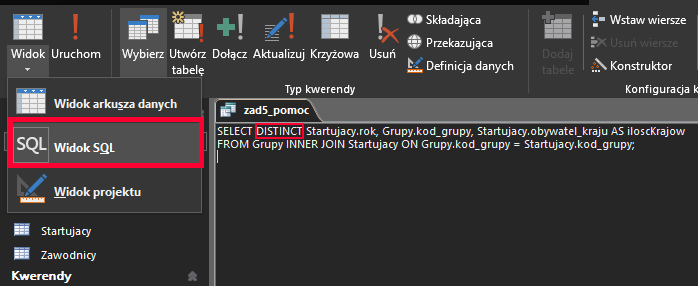
Teraz możemy wykorzystać tą kwerendę w następnej kwerendzie pomocniczej. Zliczy ona przy pomocy funkcji agregującej COUNT ile było unikalnych krajów w każdej grupie dla danego roku:
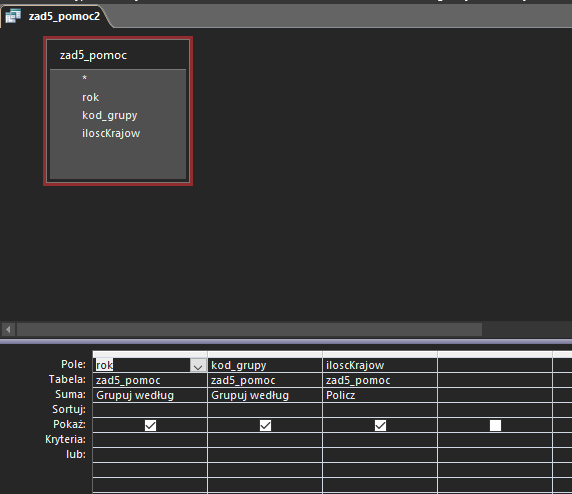
Mając już kwerendy pomocnicze możemy przejść do projektowania kwerend udzielających odpowiedzi na ten podpunkt. Zacznijmy od podania zestawienia lat i grup, w których wszyscy zawodnicy byli tej samej narodowości. Musimy zliczyć więc kraje z drugiej kwerendy pomocniczej, dla których liczba krajów była równa 1:
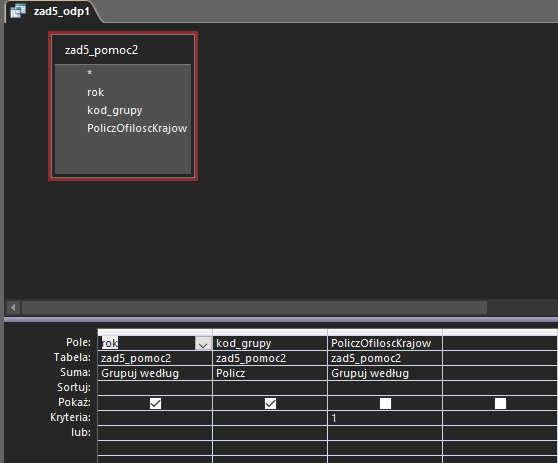
Kwerenda ta daje nam wynik:
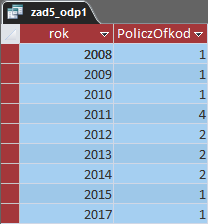
W następnym zapytaniu połączymy powyższą odpowiedź z kwerendą pomocniczą, a także z tabelą Grupy. W kwerendzie tej najpierw połączymy kolumny rok z obu kwerend przy użyciu kryterium. Następnie wybierzemy rok o największej ilości grup poprzez sortowanie malejące i ograniczenie wyników do jednego. Wyniki są od razu powiązane z tabelą grupy dzięki użyciu klucza obcego:
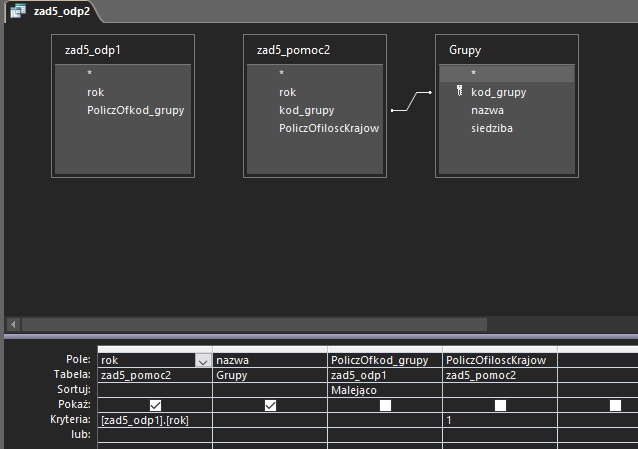
Drugą odpowiedzią jest więc poniższe zestawienie:
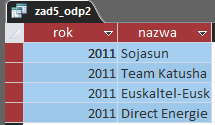
Podpunkt 6

W ostatnim zadaniu z Accessa ponownie stworzymy 3 kwerendy – dwie pomocnicze i ostatnią, dającą odpowiedź.
W pierwszej z nich powiążemy zawodnika z narodowościami, które deklarował podczas startu w wyścigu:
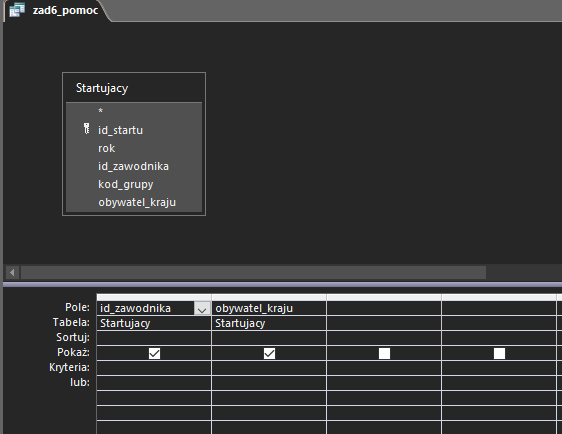
Aby jednak wyniki nie powtarzały się (bo ten sam zawodnik mógł przecież startować kilka razy jako np. Szwajcar) musimy znowu skorzystać ze słowa kluczowego DISTINCT w widoku SQL:
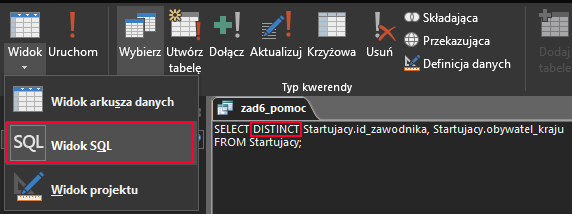
W kolejnym zapytaniu wybierzemy tych zawodników, dla których liczba narodowości jest większa niż jeden. W tym celu ponownie wykorzystamy funkcję agregującą COUNT:
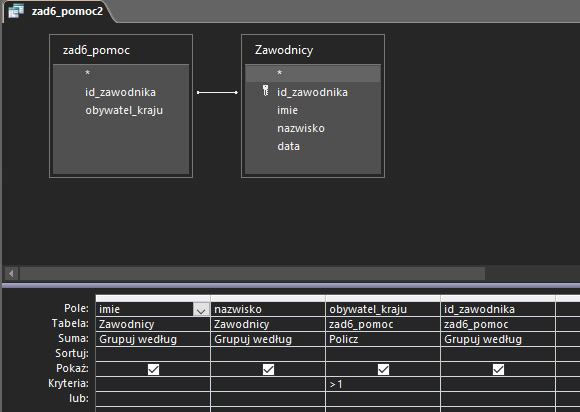
W ostatnim zapytaniu pozostaje nam już tylko powiązać wybranych przed chwilą zawodników z narodowościami deklarowanymi w tabeli startujący:
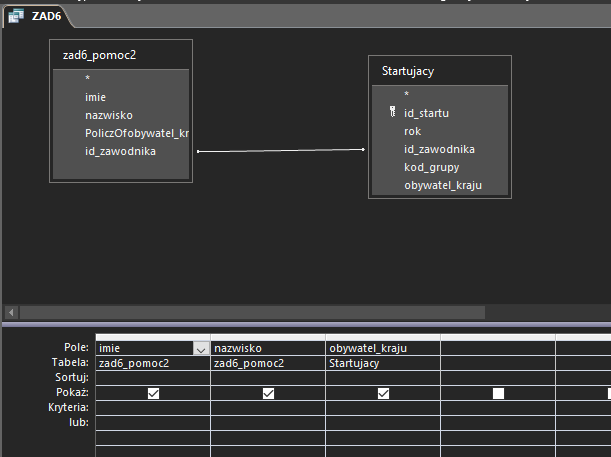
Z racji, że wybrani zawodnicy startowali kilka razy w tej samej narodowości, musimy ponownie skorzystać ze słówka DISTINCT w widoku SQL:

Tak zaprojektowana kwerenda generuje nam odpowiedź na ten podpunkt:
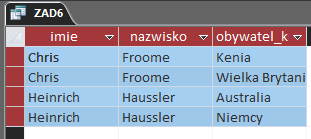
Podsumowanie
Jak więc sami widzicie tegoroczna próbna matura z informatyki nie była aż tak trudna. Przynajmniej nie tak trudna, jak jej majowe odpowiedniki z poprzednich lat. Niemniej jednak to wcale nie oznacza, że matura za miesiąc będzie łatwa, dlatego nie zwalniajcie z przygotowaniami. Powodzenia w nauce!






lel
says:Dobra robota, szacun!!