Nadszedł kolejny piątek, a wraz z nim kolejna część „Piątku z sortowaniem”. Czy jesteście gotowi na poznanie nowego algorytmu? Dziś pod lupę weźmiemy sortowanie kubełkowe (bucket sort). Bierzmy się do roboty.
Działanie
Algorytm sortowania kubełkowego jest znacznie przystępniejszy, od omawianego w poprzednim tekście sortowania binarnego. Jest on szczególnie przyjazny, w przypadku sortowania liczb całkowitych. Jak zwykle, wytłumaczmy na początku, w jaki sposób funkcjonuje ten algorytm.
Jego działanie, dzielimy na kilka prostych kroków. W pierwszym z nich, określamy dwa indeksy ymin i ymax, które mówią nam o najmniejszej i największej wartości, występującej w zbiorze. Wartości te przydadzą nam się głównie w implementacji tego algorytmu. Następnie przygotowujemy „kubełki” zliczające ilość wystąpień danych wartości w zborze. Ilość „kubełków”, możemy obliczyć ze wzoru ymin – ymax +1.
W kolejnym z kroków zliczamy liczbę wystąpień poszczególnych elementów, zwiększając wartość „kubełka” o indeksie, który odpowiada indeksowi rozpatrywanego elementu. Np. gdy natkniemy się na element o wartości 5, zwiększamy wartość „kubełeka” o indeksie 5.
W ostatnim kroku, tworzymy nowy zbiór. By tego dokonać, przechodzimy przez wszystkie liczniki, dodając do zbioru tyle poszczególnych elementów, ile ma wartość odpowiadającego mu kubełka. W ten właśnie prosty sposób otrzymamy posortowany zbiór wejściowy.

Przykład – liczby całkowite
Nic lepiej nie pomoże zrozumieć algorytmu, jak prosty przykład. Weźmy zbiór { 1, 5, 1, 5, 1, 2, 4, 5 }. W pierwszym kroku wyznaczmy ymin i ymax. Wynoszą one w tym przypadku 1 oraz 5. Tworzymy więc 5 „kubełków”:
B1 = 0, B2 = 0, B3 = 0, B4 = 0, B5 = 0
W kolejnym kroku liczymy ilość wystąpień poszczególnych elementów, zapisując je w kubełkach:
B1 = 3, B2 = 1, B3 = 0, B4 = 1, B5 = 3
Kończymy zapisując do nowego zbioru daną ilość elementów o wartościach indeksów kubełków. W ten sposób otrzymujemy: { 1,1,1,2,4,5,5,5 }. Zbiór ten odpowiada posortowanemu zbiorowi wejściowemu. By dodatkowo ułatwić zrozumienie tego procesu, spójrzcie na poniższą animację:
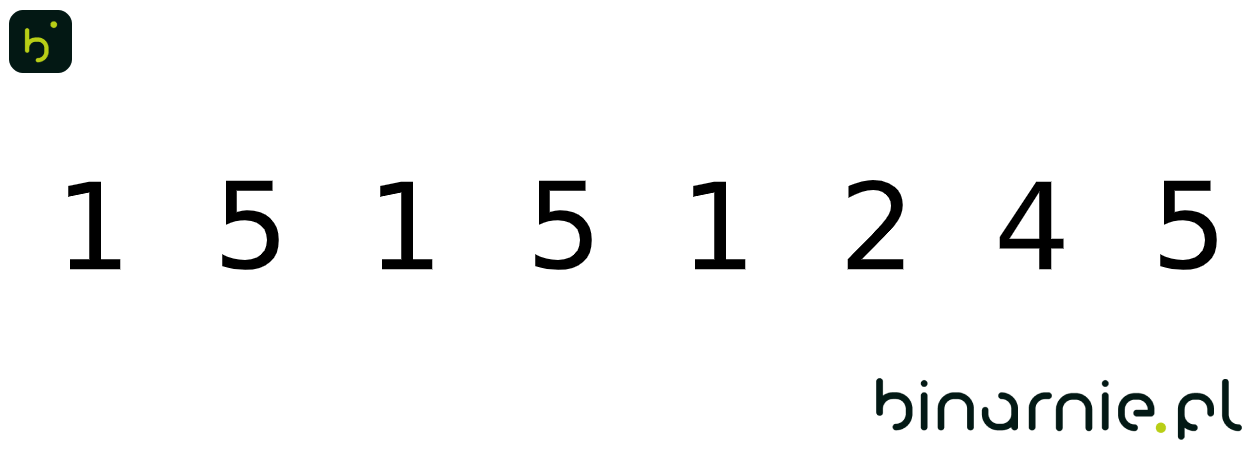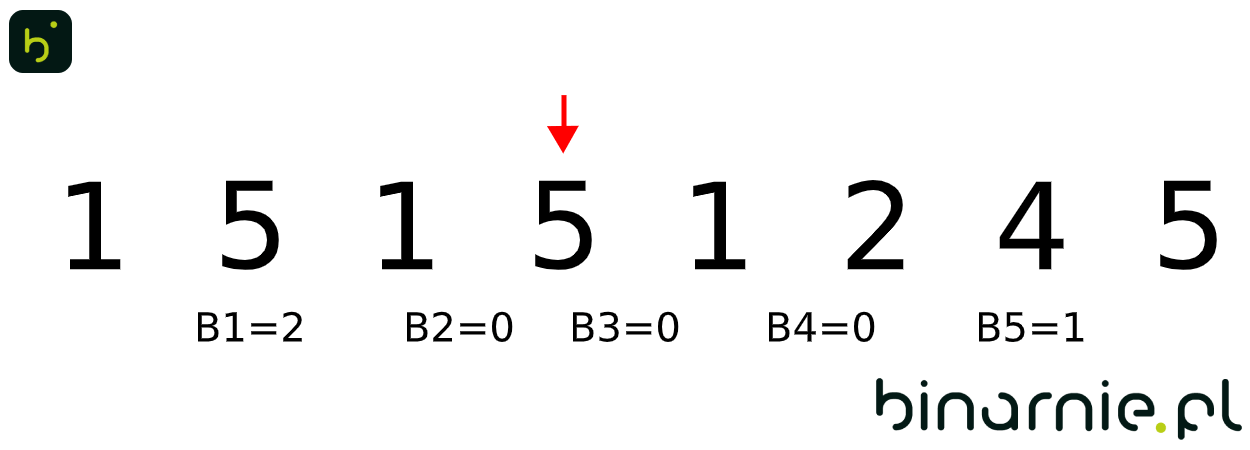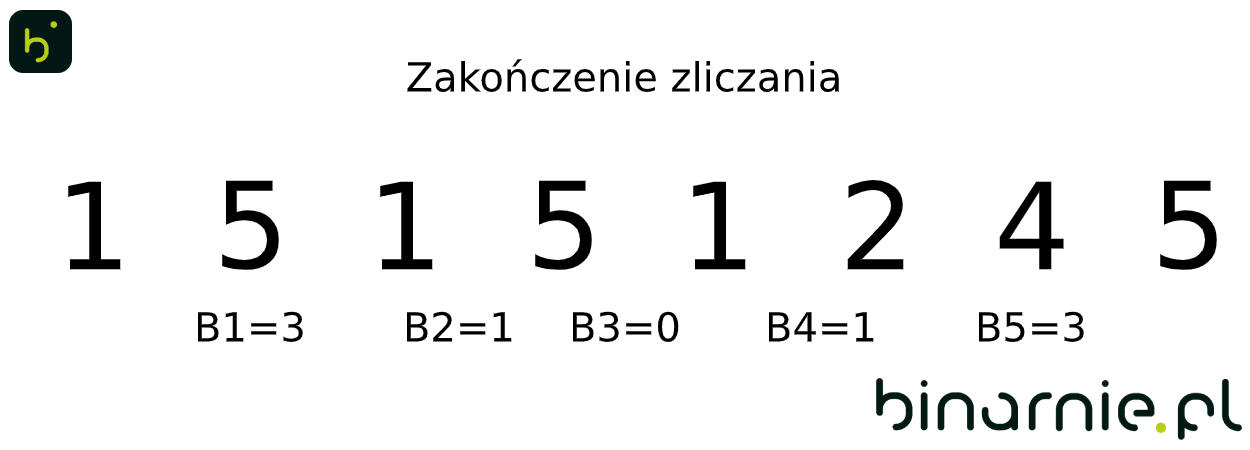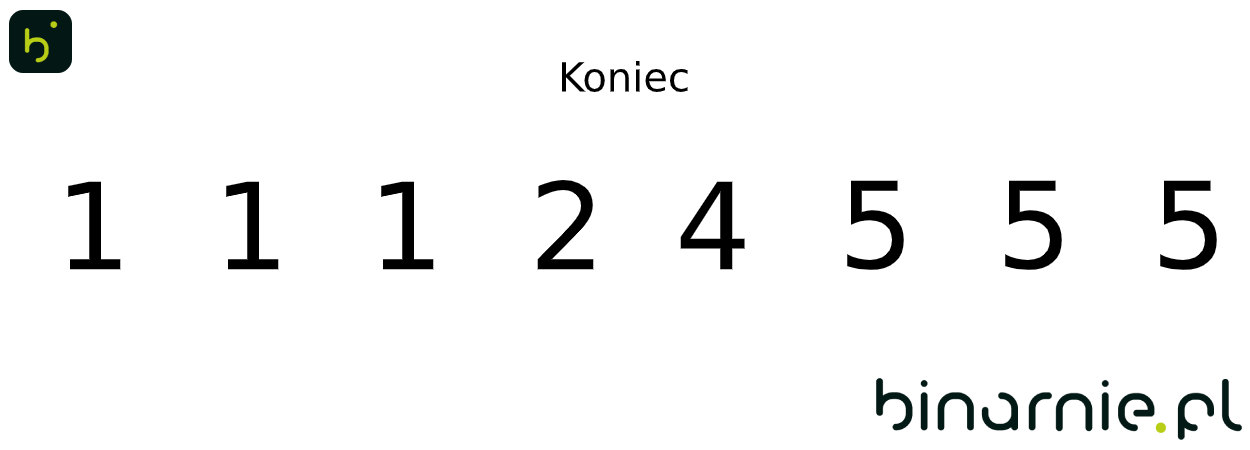
Sortowanie kubełkowe – implementacje
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 |
//program do sortowania n-elementowej tablicy //przy pomocy algorytmu sortowania kubełkowego //dla liczb całkowitych dodatnich //Jan Żwirek #include <iostream> using namespace std; void printTab(int *tab, int n); int* findMinAndMax(int* tab, int n); void bucketSort(int *tab, int n, int yMin, int yMax) { int* buckets = new int[yMax - yMin + 1]; //Wstawiamy początkowe wartości liczników for (int x = 0; x < (yMax - yMin + 1); x++) { buckets[x] = 0; } cout << endl << "Stworzono kubelki: " << endl; cout << "\t| "; for (int x = 0; x < (yMax - yMin + 1); x++) { cout << "B" << x+yMin << " | "; } cout << endl; for (int x = 0; x < n; x++) { //Zliczamy ilość wystąpień poszczególnych elementów buckets[tab[x] - yMin]++; } cout << endl << "Zliczono elementy: " << endl; cout << "\t| "; for (int x = 0; x < (yMax - yMin + 1); x++) { cout << "B" << x + yMin << "=" << buckets[x] <<" | "; } cout << endl; //Zapisujemy elementy w ilości podyktowanej przez kubełki //w tablicy int lastIndex = 0; for (int x = 0; x < (yMax - yMin + 1); x++) { int y; for (y = lastIndex; y < buckets[x] + lastIndex; y++) { tab[y] = x + yMin; } lastIndex = y; } } int main() { int n; cout << "Wprowadz liczbe elementow tablicy: "; cin >> n; //Dynamiczne tworzenie tablicy int *tab = new int[n]; cout << "\nWprowadz " << n << " liczb do posortowania" << endl; cout << "Zatwierdz kazda z nich klawiszem Enter:" << endl; for (int x = 0; x < n; x++) { cin >> tab[x]; } cout << endl << "Tablica przed posortowaniem:" << endl; printTab(tab, n); int* minAndMax = findMinAndMax(tab, n); cout << endl << "Minimalny element tablicy: " << minAndMax[0] << endl; cout << "Maksymalny element tablicy: " << minAndMax[1] << endl; cout << endl << "Rozpoczecie sortowania" << endl; bucketSort(tab, n, minAndMax[0], minAndMax[1]); cout << endl << "Oto tablica po sortowaniu:" << endl; printTab(tab, n); delete[] tab; delete[] minAndMax; system("pause"); return 0; } void printTab(int *tab, int n) { cout << endl << "\t| "; for (int x = 0; x < n; x++) { cout << tab[x] << " | "; } cout << endl << endl; } //Funkcja do wyszukiwania największej i //najmniejszej wartości w tablicy int* findMinAndMax(int* tab, int n) { int* minAndMax = new int[2]; minAndMax[0] = tab[0]; minAndMax[1] = tab[0]; for (int x = 0; x < n; x++) { if (tab[x] < minAndMax[0]) { minAndMax[0] = tab[x]; } if (tab[x] > minAndMax[1]) { minAndMax[1] = tab[x]; } } return minAndMax; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 |
package matura; import java.util.Scanner; public class Main { private static void printArray(int[] tab) { System.out.println(); for(int i = 0; i < tab.length; i++) { System.out.print(tab[i] + " | "); } System.out.println(); } private static int[] getMinMax(int[] arr) { int[] result = new int[2]; result[0] = arr[0]; // pierwszy element bedzie najmniejszym elementem result[1] = arr[0]; // drugi element bedzie najwiekszym elementem for(int i : arr) { if(result[0] > i) { //dokonujemy podmiany najwiekszego/najmniejszego elementu w przypadku gdy iterowana wartosc bedzie wieksza/mniejsza od przechowanej result[0] = i; } else if (result[1] < i) { result[1] = i; } } return result; } private static void bucketSort(int[] tab) { int[] results = getMinMax(tab); int yMax = results[1]; int yMin = results[0]; int[] buckets = new int[yMax - yMin + 1]; //Wstawiamy początkowe wartości liczników for (int x = 0; x < (yMax - yMin + 1); x++) { buckets[x] = 0; } System.out.println("Stworzono kubelki: "); for (int x = 0; x < (yMax - yMin + 1); x++) { System.out.print("B" + (x+yMin) + " | "); } System.out.println(); for (int x = 0; x < tab.length; x++) { //Zliczamy ilość wystąpień poszczególnych elementów buckets[tab[x] - yMin]++; } System.out.println("Zliczono elementy: "); for (int x = 0; x < (yMax - yMin + 1); x++) { System.out.print("B" + (x + yMin) + "=" + buckets[x] +" | "); } System.out.println(); //Zapisujemy elementy w ilości podyktowanej przez kubełki //w tablicy int lastIndex = 0; for (int x = 0; x < (yMax - yMin + 1); x++) { int y; for (y = lastIndex; y < buckets[x] + lastIndex; y++) { tab[y] = x + yMin; } lastIndex = y; } } public static void main(String[] args){ Scanner sc = new Scanner(System.in); //inicjalizujemy Scanner - obiekt pozwalajacy na wczytywanie zmiennych od uzytkownika System.out.println("Wprowadz liczbe elementow tablicy: "); int n = sc.nextInt(); int[] arr = new int[n]; for(int i = 0; i < n; i++) { System.out.println("Podaj element nr." + i + ": "); arr[i]= sc.nextInt(); //wczytujemy kolejne elementy tablicy } System.out.println("Oto wprowadzona tablica:"); printArray(arr); System.out.println(); bucketSort(arr); System.out.println(); System.out.println("Oto wprowadzona tablica po przesortowaniu:"); printArray(arr); sc.close(); //zwalniamy zasoby } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
def wypisz(tab): # tworzymy metode do wypiswania zawartosci naszej tablicy for el in tab: print(el, end=" | ") def minMax(tab): #tworzymy funkcje znajdujaca najwiekszy i najmniejszy element min = tab[0] #tworzymy zmienne pomocnicze max = tab[0] for el in tab: if el > max: # a nastepnie sprawdzamy czy sa one wieksz, lub mniejsze od iterowanej wartosci max = el if el < min: min = el array = [] array.append(min) #na koniec wrzucamy je w tablice array.append(max) return array def sortujKub(tab, n): minmax = minMax(tab) yMin = minmax[0] #wyznaczamy min i max z tablicy yMax = minmax[1] buckets = [0] * (yMax - yMin+1) #nastepnie tworzymy tablice przechowujaca kubelki print("Stworzono kubelki:") for x in range(yMax - yMin+1): print("B", (x+yMin), end=" | ") print() for x in range(n): buckets[tab[x]-yMin] += 1 #zliczamy nastepnie ilosc wystapien dla kazdego z kubelkow print("Zliczono elementy:") for x in range(yMax - yMin+1): print("B", (x+yMin), "=", buckets[x], end=" | ") print() lastIndex = 0 for x in range(yMax - yMin+1): #na koniec sortujemy podlug kubelkow tablice y = lastIndex while y < buckets[x] + lastIndex: tab[y] = x+yMin y += 1 lastIndex = y print("Podaj ilosc elementow tablicy:") a = int(input()) tablica = [] for i in range(a): print("Podaj element nr. ", (i + 1)) tablica.append(int(input())) print("Oto twoja tablica:") wypisz(tablica) sortujKub(tablica, a) print("Oto twoja tablica po sortowaniu:") wypisz(tablica) |
Przykład – liczby ułamkowe
Sortowanie kubełkowe nie służy jednak tylko i wyłącznie do sortowania liczb całkowitych. Można nim sortować także liczby typu float. Tu sprawa robi się jednak nieco bardziej skomplikowana. Podobnie jak w przypadku liczb całkowitych, tworzyć będziemy „kubełki”. Tym razem, nie będą one jedynie licznikami, a będą strukurami przechowującymi wartości w wyznaczonych zakresach. Przykładowo, kubełek o indeksie 0, będzie przechowywał liczby w zakresie [0, 1). Nie wystarczy nam więc jedynie dodać liczby do kubełków. W końcowym kroku należy posortować poszczególne kubełki, przy pomocy innego algorytmu sortowania np. sortowaniem przez wstawianie, który również omawialiśmy w „Piątku z sortowaniem”.
Poszczególne kroki będą więc wyglądać w następujący sposób:
- Wyznaczamy ymin i ymax
- Tworzymy kubełki będące podzakresami
- Dodajemy poszczególne elementy zbioru do kubełków
- Sortujemy wszystkie kubełki
- Zapisujemy po kolei elementy ze wszystkich kubełków
Przykład – ułamki
Weźmy zbiór {0.48, 0.27, 0.12, 0.21, 0.43, 0.25}. W pierwszej kolejności wyznaczymy ymin i ymax, wynoszące 0.12 i 0.48, a następnie stwórzmy kubełki:
B1 = {}, B2 = {}, B3 = {}, B4 = {}
Kolejno umieszczamy każdy z elementów w kubełku, którego zakres odpowiada wartości danego elementu:
B1 = {0.12}, B2 = {0.27, 0.21, 0.25}, B3 = {}, B4 = {0.48, 0.43}
Jak zapewne widzicie, kubełki wymagają sortowania. To więc właśnie zrobimy:
B1 = {0.12}, B2 = {0.21, 0.25, 0.27}, B3 = {}, B4 = {0.43, 0.48}
W ostatnim kroku, łączymy wszystkie kubełki w nowy zbiór, otrzymując posortowany zbiór wejściowy mający postać {0.12, 0.21, 0.25, 0.27, 0.43, 0.48}.
Spójrzmy więc na animację, obrazującą działanie algorytmu w podanym przypadku:
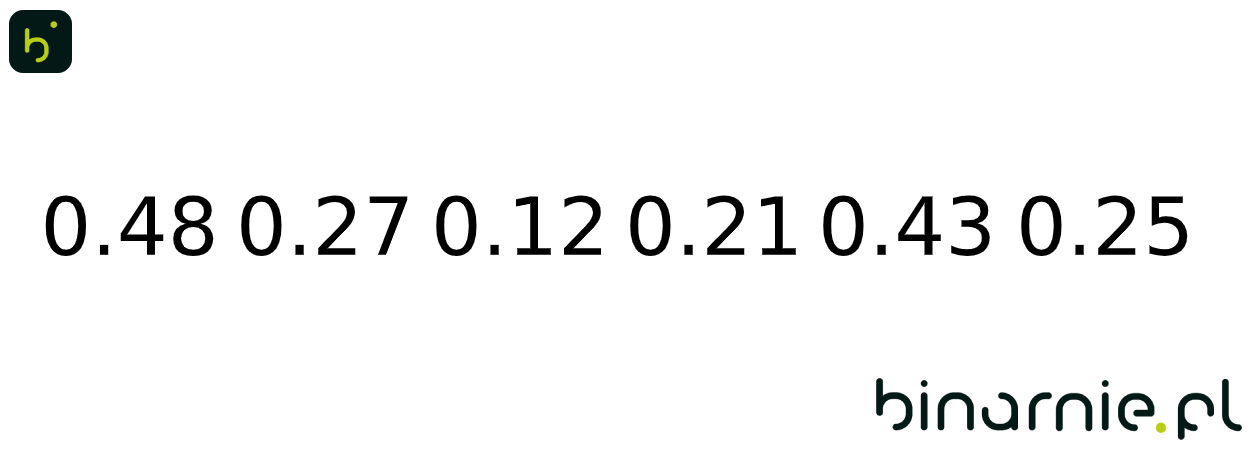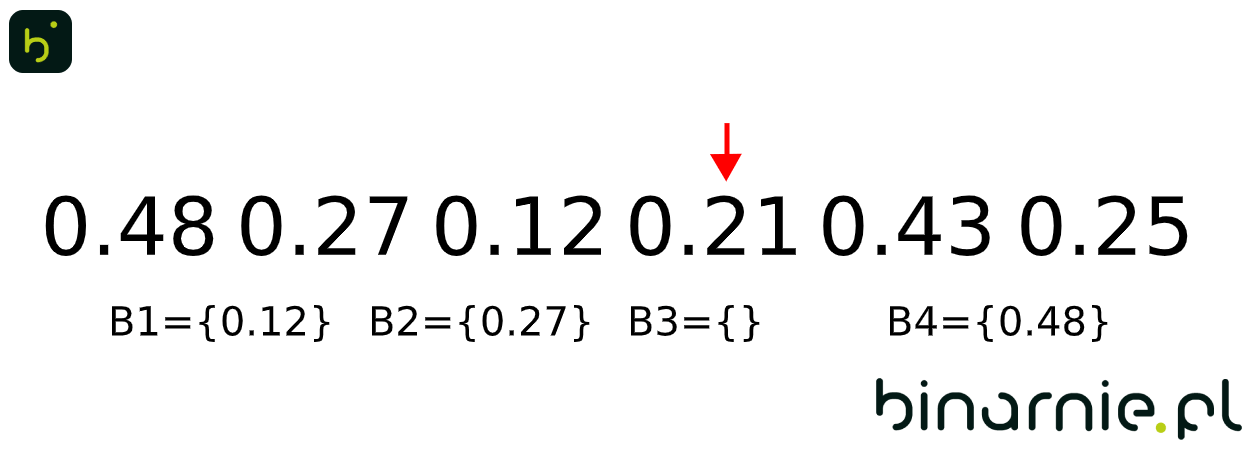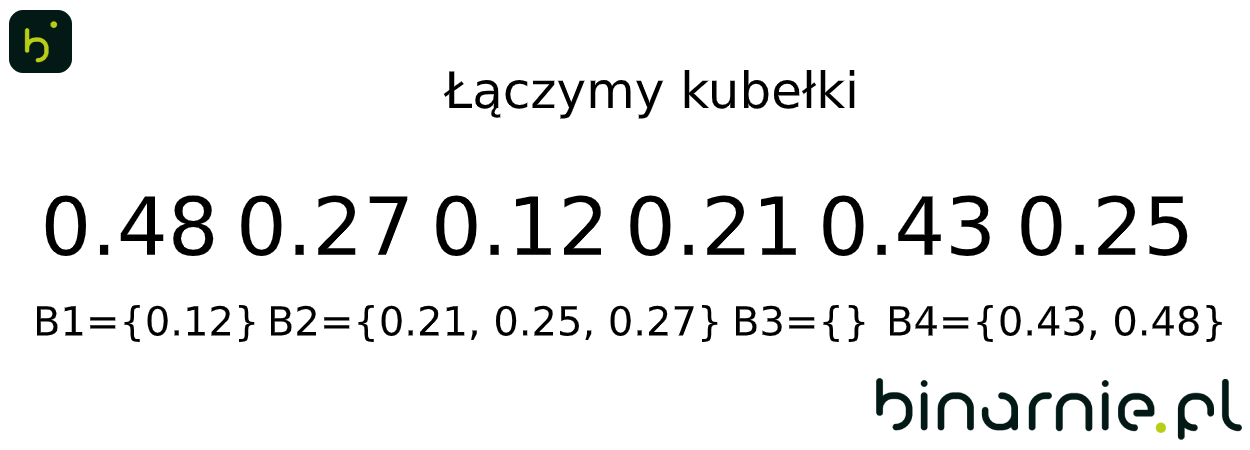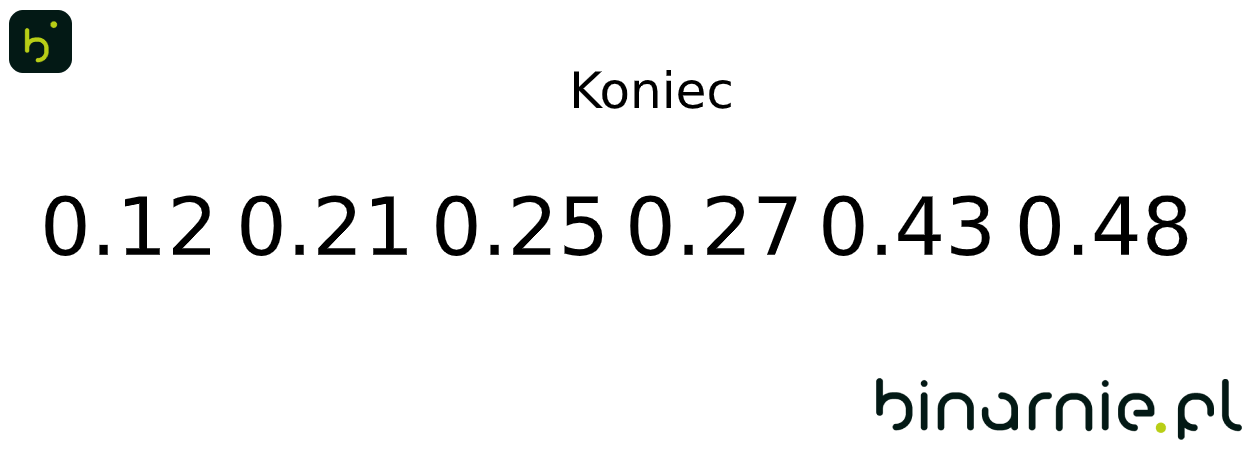
Sortowanie kubełkowe dla ułamków dziesiętnych – implementacje
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 |
//program do sortowania n-elementowej tablicy //przy pomocy algorytmu sortowania kubełkowego //dla liczb ułamkowych //Jan Żwirek #include "pch.h" #include <iostream> #include <vector> using namespace std; void printTab(float *tab, int n); void printVectors(vector<float> vectors[], int numberOfVectors, int yMinIndex); float* findMinAndMax(float* tab, int n); void insertionSort(vector<float> *tab, int n); void bucketSort(float *tab, int n, float yMin, float yMax) { int yMinIdex = yMin * 10; int yMaxIndex = yMax * 10; int numberOfBuckets = yMaxIndex - yMinIdex + 1; //Tworzymy odpowiednią ilość kubełków vector<float> * buckets = new vector<float>[numberOfBuckets]; cout << endl << "Stworzono kubelki: " << endl; cout << "\t| "; for (int x = 0; x < numberOfBuckets; x++) { cout << "B" << x + yMinIdex << " | "; } cout << endl; for (int x = 0; x < n; x++) { int insertIndex = (tab[x] * 10) - yMinIdex; buckets[insertIndex].push_back(tab[x]); } cout << endl << "Elementy w kubelkach: " << endl; printVectors(buckets, numberOfBuckets, yMinIdex); //Sortujemy kubełki korzystajac z wczesniej zaimplementowanego //i lekko zmodyfikowanego sortowania przez wstawianie for (int x = 0; x < numberOfBuckets; x++) { insertionSort(&buckets[x], buckets[x].size()); } cout << endl << "Kubelki po posortowaniu:" << endl; printVectors(buckets, numberOfBuckets, yMinIdex); //Zapisujemy elementy w ilości podyktowanej przez kubełki //w tablicy int lastIndex = 0; for (int x = 0; x < numberOfBuckets; x++) { int y; for (y = 0; y < buckets[x].size(); y++) { tab[y + lastIndex] = buckets[x].at(y); } lastIndex += y; } } int main() { int n; cout << "Wprowadz liczbe elementow tablicy: "; cin >> n; //Dynamiczne tworzenie tablicy float *tab = new float[n]; cout << "\nWprowadz " << n << " liczb do posortowania" << endl; cout << "Zatwierdz kazda z nich klawiszem Enter:" << endl; for (int x = 0; x < n; x++) { cin >> tab[x]; } cout << endl << "Tablica przed posortowaniem:" << endl; printTab(tab, n); float* minAndMax = findMinAndMax(tab, n); cout << endl << "Minimalny element tablicy: " << minAndMax[0] << endl; cout << "Maksymalny element tablicy: " << minAndMax[1] << endl; cout << endl << "Rozpoczecie sortowania" << endl; bucketSort(tab, n, minAndMax[0], minAndMax[1]); cout << endl << "Oto tablica po sortowaniu:" << endl; printTab(tab, n); delete[] tab; delete[] minAndMax; system("pause"); return 0; } void printTab(float *tab, int n) { cout << endl << "\t| "; for (int x = 0; x < n; x++) { cout << tab[x] << " | "; } cout << endl << endl; } //Funkcja do wyszukiwania największej i //najmniejszej wartości w tablicy float* findMinAndMax(float* tab, int n) { float* minAndMax = new float[2]; minAndMax[0] = tab[0]; minAndMax[1] = tab[0]; for (int x = 0; x < n; x++) { if (tab[x] < minAndMax[0]) { minAndMax[0] = tab[x]; } if (tab[x] > minAndMax[1]) { minAndMax[1] = tab[x]; } } return minAndMax; } void insertionSort(vector<float> *tab, int n) { for (int x = 1; x < n; x++) { //Wybieramy element który chcemy porównywać float selectedElement = tab->at(x); //Rozpoczynamy przesuwanie elementów szukając miesjca docelowego //dla wybranego przez nas elementu for (int y = x-1; y >= 0; y--) { if (selectedElement < tab->at(y)) { //Funkcja zamieniająca dwa elementy miejscami iter_swap(tab->begin() + y, tab->begin() + y + 1); } } } } void printVectors(vector<float> vectors[], int numberOfVectors, int yMinIndex) { cout << "\t| "; for (int x = 0; x < numberOfVectors; x++) { cout << "B" << x + yMinIndex << "= {"; for (float y : vectors[x]) { cout << y << ", "; } cout << "} | "; } cout << endl; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 |
package matura; import java.util.ArrayList; import java.util.Collections; import java.util.HashMap; import java.util.Scanner; public class Main { private static void printArray(float[] tab) { System.out.println(); for(int i = 0; i < tab.length; i++) { System.out.print(tab[i] + " | "); } System.out.println(); } private static float[] getMinMax(float[] arr) { float[] result = new float[2]; result[0] = arr[0]; // pierwszy element bedzie najmniejszym elementem result[1] = arr[0]; // drugi element bedzie najwiekszym elementem for(float i : arr) { if(result[0] > i) { //dokonujemy podmiany najwiekszego/najmniejszego elementu w przypadku gdy iterowana wartosc bedzie wieksza/mniejsza od przechowanej result[0] = i; } else if (result[1] < i) { result[1] = i; } } return result; } private static void insertionSort(ArrayList<Float> tab) { for (int x = 1; x < tab.size(); x++) { //Wybieramy element który chcemy porównywać float selectedElement = tab.get(x); //Rozpoczynamy przesuwanie elementów szukając miesjca docelowego //dla wybranego przez nas elementu for (int y = x-1; y >= 0; y--) { if (selectedElement < tab.get(y)) { //Funkcja zamieniająca dwa elementy miejscami Collections.swap(tab, y, y+1); } } } } private static void bucketSort(float[] tab) { float[] results = getMinMax(tab); int yMax = (int) (results[1] * 10); int yMin = (int) (results[0] * 10); int bucketsAmount = yMax - yMin + 1; HashMap<Integer, ArrayList<Float>> buckets = new HashMap<Integer, ArrayList<Float>>(); //Wstawiamy początkowe wartości liczników System.out.println("Stworzono kubelki: "); for (int x = 0; x < (yMax - yMin + 1); x++) { buckets.put(x, new ArrayList<Float>()); System.out.print("B" + (x+yMin) + " | "); } System.out.println(); for (int x = 0; x < tab.length; x++) { int insertIndex = (int) ((tab[x] * 10) - yMin); buckets.get(insertIndex).add(tab[x]); } System.out.println("Elementy w kubelkach: "); for (int x = 0; x < (yMax - yMin + 1); x++) { System.out.println("B" + (x + yMin) + "=" + buckets.get(x).size() +" | "); for(float element : buckets.get(x)) { System.out.println(element); } } System.out.println(); //Sortujemy kubełki korzystajac z wczesniej zaimplementowanego //i lekko zmodyfikowanego sortowania przez wstawianie for(int i = 0; i < bucketsAmount; i++) { insertionSort(buckets.get(i)); } System.out.println("Elementy w kubelkach po sortowaniu: "); for (int x = 0; x < (yMax - yMin + 1); x++) { System.out.println("B" + (x + yMin) + "=" + buckets.get(x).size() +" | "); for(float element : buckets.get(x)) { System.out.println(element); } } System.out.println(); //Zapisujemy elementy w ilości podyktowanej przez kubełki //w tablicy int lastIndex = 0; for (int x = 0; x < bucketsAmount; x++) { int y; for (y = 0; y < buckets.get(x).size(); y++) { tab[y + lastIndex] = buckets.get(x).get(y); } lastIndex += y; } } public static void main(String[] args){ Scanner sc = new Scanner(System.in); //inicjalizujemy Scanner - obiekt pozwalajacy na wczytywanie zmiennych od uzytkownika System.out.println("Wprowadz liczbe elementow tablicy: "); int n = sc.nextInt(); float[] arr = new float[n]; for(int i = 0; i < n; i++) { System.out.println("Podaj element nr." + i + ": "); arr[i]= sc.nextFloat(); //wczytujemy kolejne elementy tablicy } System.out.println("Oto wprowadzona tablica:"); printArray(arr); System.out.println(); bucketSort(arr); System.out.println(); System.out.println("Oto wprowadzona tablica po przesortowaniu:"); printArray(arr); sc.close(); //zwalniamy zasoby } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
def wypisz(tab): # tworzymy metode do wypiswania zawartosci naszej tablicy for el in tab: print(el, end=" | ") def insertionSort(tab): #wykorzystujemy lekko zmodyfikowany algoprytm sorotwania przez wstawianie for x in range(1, len(tab)): element = tab[x] y = x-1 while y >= 0: if element < tab[y]: pom = tab[y+1] tab[y+1] = tab[y] tab[y] = pom y -= 1 def minMax(tab): #tworzymy funkcje znajdujaca najwiekszy i najmniejszy element min = tab[0] #tworzymy zmienne pomocnicze max = tab[0] for el in tab: if el > max: # a nastepnie sprawdzamy czy sa one wieksz, lub mniejsze od iterowanej wartosci max = el if el < min: min = el array = [] array.append(min) #na koniec wrzucamy je w tablice array.append(max) return array def wypiszKubelek(kub, n): #pomocnicza funkcja do wypisywanai kubelkow i ich zawartosci print("B", n, "=", len(kub), end=" => ") for element in kub: print(element, end=" | ") print() def sortujKub(tab, n): minmax = minMax(tab) yMin = int(minmax[0] * 10) #wyznaczamy min i max z tablicy yMax = int(minmax[1] * 10) bucketsAmount = yMax - yMin + 1 #liczymy ilosc kubelkow buckets = {} #tworzymy mape przechowujaca kubelki i listy elementow print("Stworzono kubelki:") for x in range(bucketsAmount): #wypelniamy mape jednoczesnie wypisujac stworzone kubelki buckets[x] = [] print("B", (x+yMin), end=" | ") print() for x in range(n): #nastepnie przyporzadkowujemy elementy do odpowiednich kubelkow insertIndex = int(tab[x] * 10 - yMin) buckets[insertIndex].append(tab[x]) print("Elementy w kubelkach: ") for x in range(bucketsAmount): #wypisujemy kazdy kubelek uzytkownikowi, po czym od razu go sortujemy wypiszKubelek(buckets[x], x+yMin) insertionSort(buckets[x]) print() print("Elementy w kubelkach po przesortowaniu: ") for x in range(bucketsAmount): #nastepnie wypisujemy posortowane juz kubelki wypiszKubelek(buckets[x], x+yMin) print() lastIndex = 0 for x in range(bucketsAmount): #po czym mozemy przystapic do wstawiania ich w wyjsciowa tablice z = 0 for y in range(len(buckets[x])): tab[y+lastIndex] = buckets[x][y] z += 1 lastIndex += z print("Podaj ilosc elementow tablicy:") a = int(input()) tablica = [] for i in range(a): print("Podaj element nr. ", (i + 1)) tablica.append(float(input())) print("Oto twoja tablica:") wypisz(tablica) sortujKub(tablica, a) print("Oto twoja tablica po sortowaniu:") wypisz(tablica) |
Trochę teorii
Jest to niezwykle ciekawy algorytm, ze względu na swoją efektywność. Sortowanie kubełkowe, radzi sobie najlepiej ze zbiorami o dużej ilości elementów, lecz małym zakresie wartości. W przypadku zbioru stosunkowo małym zakresie, i dużej ilości elementów, algorytm ten będzie niezwykle efektywny, dążąc do optymistycznej złożoności O(n).
Niestety w pesymistycznym przypadku, ma on złożoność rzędu O(n2), czyli taką jak chociażby niesławne sortowanie bąbelkowe, którego opis znajdziecie tutaj.
Podsumowanie
Za nami kolejny algorytm sortowania, tym razem z dwoma implementacjami. Za tydzień spotykamy się ponownie, by poznać następny! Zapraszamy Was również na naszą facebookową grupę, na której znajdziecie materiały pomocnicze do matury z informatyki, dotyczące nie tylko algorytmów.






mike_Y
says:Cześć! Jestem uczniem liceum i akurat szukałem algorytmów sortujących ucząc się do matury. Trafiłem na twoją stronę. Przeczytałem artykuł, zrozumiałem algorytm, napisałem program, a następnie zdziwiłem się o ile jest krótszy od Twojego przykładowego. Czy to ja popełniłem gdzieś błąd? A może Ty napisałeś go specjalnie troszkę rozwleklej aby każdy go zrozumiał? Pozdrawiam!
Poniżej wklejam moje rozwiązanie problemu w Pythonie 🙂
from random import randrange as rr
from pprint import pprint as pp
tab = [rr(7) for i in range(20)]
print(tab)
def sortowanie_kubelkowe(tab):
dict = {letter: tab.count(letter) for letter in set(tab)}
tab.clear()
for value, number_of_appearance in dict.items():
for i in range(number_of_appearance):
tab.append(value)
return tab ,dict
print(sortowanie_kubelkowe(tab))
msy
says:Pominięto chyba najważniejsze zastosowanie sortowania kubełkowego – porządkowanie ciągów znaków, słów nad jakimś alfabetem i to dowolnej i różnej długości. Szczegóły w M.M.Sysło, Algorytmy, Helion 2016.