Czyżby nadszedł ten najbardziej wyczekiwany dzień tygodnia? Jak sami wiecie, wraz z nim obowiązkowo pojawia się kolejna część „Piątku z sortowaniem”. Po małym „spinoffie” z prezentacją gotowych metod sortowania w C++ i Javie, wracamy do klasyki. Tym razem dowiemy się czym jest sortowanie przez scalanie (merge sort). Jesteście gotowi?
Sortowanie przez scalanie – algorytm
Algorytm sortowania przez scalanie, to kolejny już z algorytmów, który opiera się na zasadzie „dziel i zwyciężaj”. Można wręcz powiedzieć, że wykorzystuje ją w dość bezpośrednim rozumieniu. Główna zasada działania polega na rekurencyjnym dzieleniu tablicy na podtablice. Dzielenie kończymy, w którym, każda z podtablic w danej grupie jest tablicą jednoelementową. Łączymy je kolejno porównując wartości ich elementów. Dokładny przebieg algorytmu wygląda następująco:
Jeśli indeks prawej części tablicy (r) jest większy od indeksu lewej (l) części tablicy wykonaj następujące kroki:
- Znajdź środkowy indeks tablicy (m), ze wzoru m=(l+r)/2 (resztę z dzielenia zaokrąglamy w dół)
- Wywołaj sortowanie przez scalanie dla podtablicy o indeksach od l do m
- Wywołaj sortowanie przez scalanie dla podtablicy o indeksach od m+1 do r
- Połącz podtablicę l – m i m+1 – r, przyrównując przy tym ich elementy – Jeśli element lewej tablicy na aktualnej pozycji jest mniejszy od tego na prawej, wstaw go do tablicy docelowej i zwiększ indeks lewej tablicy. W przeciwnym przypadku, wykonaj analogiczne działanie dla prawej tablicy.
Sortowanie przez scalanie – przykład
Aby lepiej zwizualizować sobie zasadę działania algorytmu, prześledźmy prosty przykład. Weźmy zbiór { 4, 2, 8, 6, 5, 1 }. W pierwszej kolejności wyznaczamy indeksy l,r i m:
l = 0
r = 5
m = 2
Następnie dzielimy zbiór wejściowy na dwie podtablice:
L = { 4, 2, 8 } P = { 6, 5, 1 }
Ponownie wykonujemy kolejne podziały lewej podtablicy, do momentu otrzymania następujących zbiorów:
L = ({ 4 }, { 2 }, { 8 }) P = { 6, 5, 1 }
Łączymy elementy lewej części podzbiorów, ustawiając je w porządku rosnącym:
L = { 2,4,8 } P = { 6, 5, 1 }
Wykonujemy podział dla prawej podtablicy:
L = { 2,4,8 } P = ({ 6 }, { 5 }, { 1 })
Łączymy elementy prawej części podtablicy:
L = { 2,4,8 } P = { 1, 5, 6 }
Łączymy obie podtablice:
{1, 2, 4, 5, 6, 8}
W taki sposób otrzymujemy posortowany zbiór wejściowy. By w pełni zrozumieć zasadę działania algorytmu, spójrzcie na poniższą animację:G
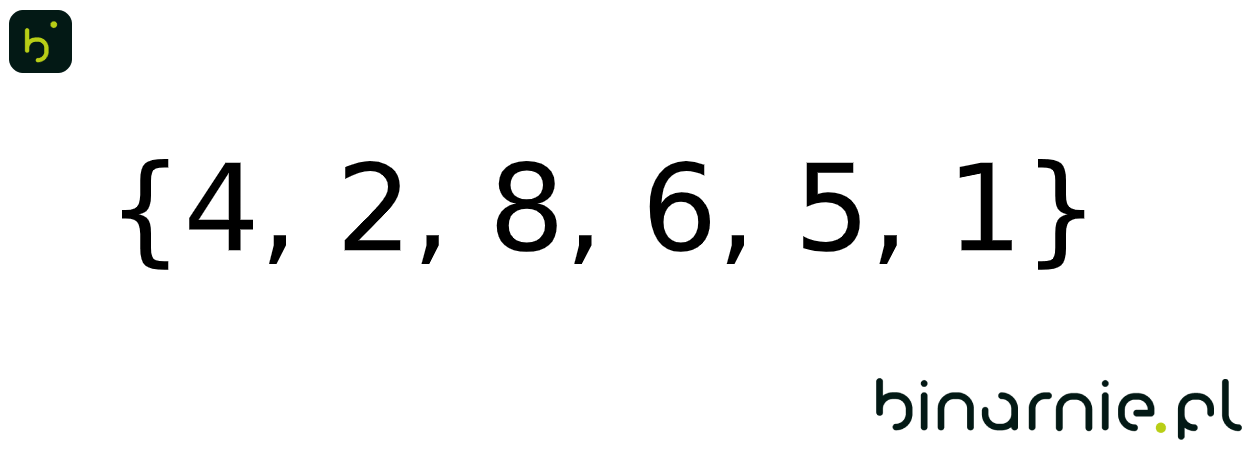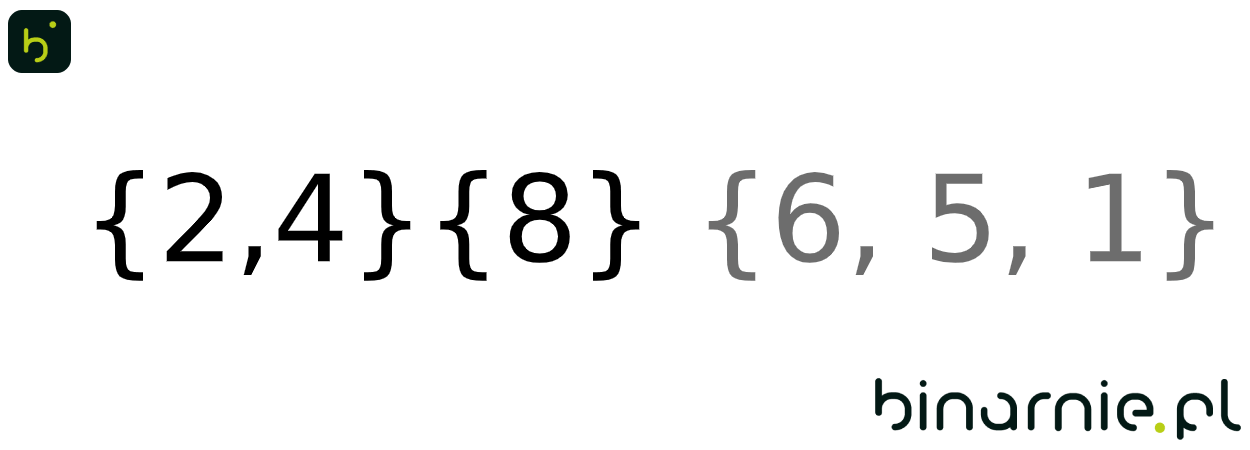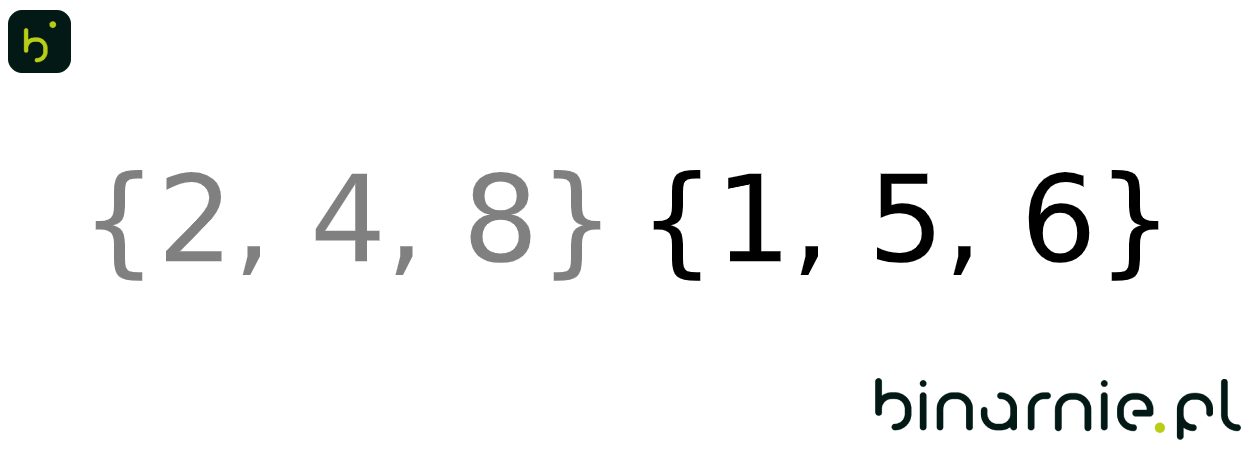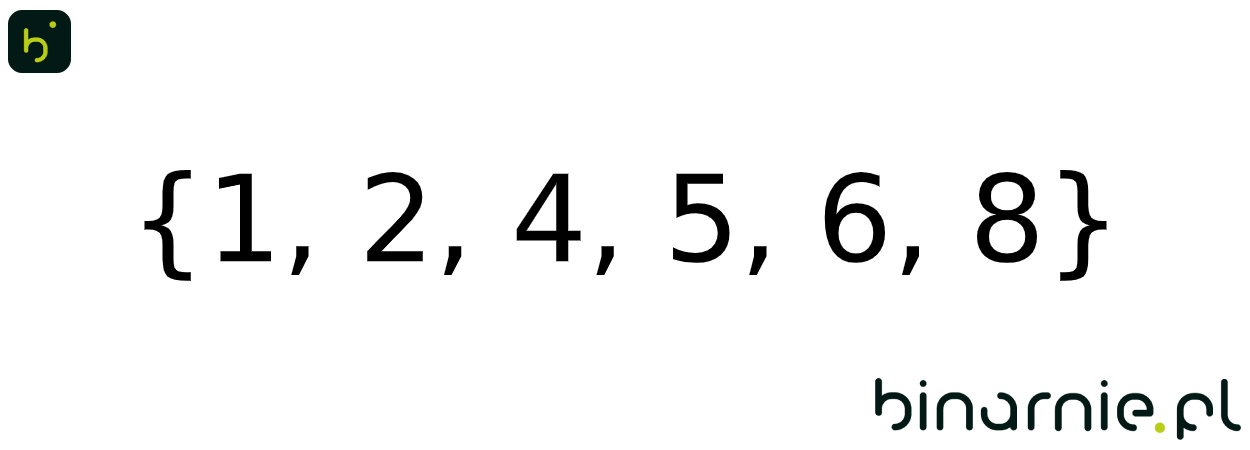
Sortowanie przez scalanie – implementacje
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 |
//program do sortowania n-elementowej tablicy //przy pomocy algorytmu sortowania przez scalanie //Jan Żwirek #include <iostream> using namespace std; void printTab(int* tab, int n); void merge(int* tab, int l, int m, int r) { int lSize = m - l + 1; int rSize = r - m; //Tablice pomocnicze int* tabL = new int[lSize]; int* tabR = new int[rSize]; // Kopiowanie danych do tablic pomocniczych for (int x = 0; x < lSize; x++) tabL[x] = tab[l + x]; for (int y = 0; y < rSize; y++) tabR[y] = tab[m + 1 + y]; int indexL = 0; int indexR = 0; int currIndex; //Łączenie tablic R i L for (currIndex = l; indexL < lSize && indexR < rSize; currIndex++) { if (tabL[indexL] <= tabR[indexR]) tab[currIndex] = tabL[indexL++]; else tab[currIndex] = tabR[indexR++]; } //Jeśli w tablicy tabL pozostały jeszcze jakieś elementy //kopiujemy je while (indexL < lSize) tab[currIndex++] = tabL[indexL++]; //Jeśli w tablicy tabR pozostały jeszcze jakieś elementy //kopiujemy je while (indexR < rSize) tab[currIndex++] = tabR[indexR++]; delete[] tabL; delete[] tabR; } void mergeSort(int* tab, int l, int r) { if (r > l) { int m = (l + r) / 2; mergeSort(tab, l, m); mergeSort(tab, m + 1, r); merge(tab, l, m, r); } } int main() { int n; cout << "Wprowadz liczbe elementow tablicy: "; cin >> n; //Dynamiczne tworzenie tablicy int* tab = new int[n]; cout << "\nWprowadz " << n << " liczb do posortowania" << endl; cout << "Zatwierdz kazda z nich klawiszem Enter:" << endl; for (int x = 0; x < n; x++) { cin >> tab[x]; } cout << endl << "Tablica przed posortowaniem:" << endl; printTab(tab, n); cout << endl << "Rozpoczecie sortowania" << endl; mergeSort(tab, 0, n-1); cout << endl << "Oto tablica po sortowaniu:" << endl; printTab(tab, n); delete[] tab; system("pause"); return 0; } void printTab(int* tab, int n) { cout << endl; for (int x = 0; x < n; x++) { cout << tab[x] << " | "; } cout << endl; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 |
package matura; import java.util.Scanner; public class Main { private static void printArray(int[] tab) { System.out.print("| "); for(int i = 0; i < tab.length; i++) { System.out.print(tab[i] + " | "); } System.out.println(); System.out.println(); } private static void merge(int[] tab, int l, int m, int r) { int lSize = m - l + 1; int rSize = r - m; //Tablice pomocnicze int[] tabL = new int[lSize]; int[] tabR = new int[rSize]; // Kopiowanie danych do tablic pomocniczych for (int x = 0; x < lSize; x++) tabL[x] = tab[l + x]; for (int y = 0; y < rSize; y++) tabR[y] = tab[m + 1 + y]; int indexL = 0; int indexR = 0; int currIndex; //Łączenie tablic R i L for (currIndex = l; indexL < lSize && indexR < rSize; currIndex++) { if (tabL[indexL] <= tabR[indexR]) tab[currIndex] = tabL[indexL++]; else tab[currIndex] = tabR[indexR++]; } //Jeśli w tablicy tabL pozostały jeszcze jakieś elementy //kopiujemy je while (indexL < lSize) tab[currIndex++] = tabL[indexL++]; //Jeśli w tablicy tabR pozostały jeszcze jakieś elementy //kopiujemy je while (indexR < rSize) tab[currIndex++] = tabR[indexR++]; } private static void mergeSort(int[] tab, int l, int r) { if (r > l) { int m = (l + r) / 2; mergeSort(tab, l, m); mergeSort(tab, m + 1, r); merge(tab, l, m, r); } } public static void main(String[] args){ Scanner sc = new Scanner(System.in); //inicjalizujemy Scanner - obiekt pozwalajacy na wczytywanie zmiennych od uzytkownika System.out.println("Wprowadz liczbe elementow tablicy: "); int n = sc.nextInt(); int[] arr = new int[n]; for(int i = 0; i < n; i++) { System.out.println("Podaj element nr." + i + ": "); arr[i]= sc.nextInt(); //wczytujemy kolejne elementy tablicy } System.out.println("Oto wprowadzona tablica:"); printArray(arr); System.out.println(); mergeSort(arr, 0, n-1); System.out.println(); System.out.println("Oto wprowadzona tablica po przesortowaniu:"); printArray(arr); sc.close(); //zwalniamy zasoby } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
def wypisz(tab): # tworzymy metode do wypiswania zawartosci naszej tablicy for el in tab: print(el, end=" | ") def scal(tab, n, m, r): #tworzymy funkcje scalajaca zbiory lsize = m - n + 1 #obliczamy wielkosci zbiorow rsize = r - m left = [0] * lsize #i tworzymy tablice pomocnicze right = [0] * rsize for x in range(lsize): #kopiujemy dane do tablic pomocniczych left[x] = tab[n + x] for y in range(rsize): right[y] = tab[m + y + 1] leftIndex = 0 #tworzymy pomocnicze zmienne przechowujace indexy rightIndex = 0 currIndex = n while leftIndex < lsize and rightIndex < rsize: #a nastepnie z ich pomoca laczymy prawa i lewa tablice if left[leftIndex] <= right[rightIndex]: tab[currIndex] = left[leftIndex] leftIndex += 1 else: tab[currIndex] = right[rightIndex] rightIndex += 1 currIndex += 1 while leftIndex < lsize: #jezeli w lewej tablicy zostaly jeszcze jakies elementy tab[currIndex] = left[leftIndex] #kopiujemy je do wyjsciowej currIndex += 1 leftIndex += 1 while rightIndex < rsize: #jezeli w prawej tablicy zostaly jeszcze jakies elementy tab[currIndex] = right[rightIndex] #kopiujemy je do wyjsciowej currIndex += 1 rightIndex += 1 def sortujScalanie(tab, l, r): if r > l: m = int((l + r) / 2) sortujScalanie(tab, l, m) sortujScalanie(tab, m + 1, r) scal(tab, l, m, r) print("Podaj ilosc elementow tablicy:") a = int(input()) tablica = [] for i in range(a): print("Podaj element nr. ", (i + 1)) tablica.append(int(input())) print("Oto twoja tablica:") wypisz(tablica) sortujScalanie(tablica, 0, a - 1) print("Oto twoja tablica po sortowaniu:") wypisz(tablica) |
Nieco teorii
Algorytm sortowania, został odkryty przez legendarnego matematyka i informatyka Johna von Neumanna. Jego złożoność czasowa ma wartość O(nlog(n)), co jest bardzo dobrym wynikiem. Jest on bardzo popularny w przypadku sortowania wszelkiego rodzaju list. Możliwe, że wiele z was wykorzystywało go, bez świadomości o jego istnieniu. Jest wykorzystywany m.in. w funkcji Collections.sort() w jęzuku Java.
Podsumowanie
Właśnie wspólnie poznaliśmy zasadę działania sortowania przez scalanie. Znajomość tego popularnego algorytmu, z pewnością przyda Wam się w zrozumieniu wielu funkcji sortowania.

Ku mojej wielkiej przykrości, muszę ogłosić koniec serii „Piątku z sortowaniem”. Nie oznacza to jednak końca pojawiania się materiałów na binarnie.pl! Szykujemy dla Was wiele ciekawych wpisów, które już niedługo ujrzą światło dzienne. Trzymajcie się i do zobaczenia już niedługo!






user2341
says:Ze wszystkich stron z algorytmami ta jest najmniej czytelna.