Repertuar sortowań jest bardzo szeroki i warto kojarzyć podstawowe z nich, zwłaszcza przygotowując się do matury. Tekst ten otwiera serię „Piątek z sortowaniem”, gdzie zapoznamy się z najpopularniejszymi algorytmami sortowania. W tej części dowiemy się jak działa sortowanie przez wybór.
Zasada działania
Algorytm selection sort nie należy do przesadnie skomplikowanych, więc nie trzeba się go obawiać. Sedno jego działania można ująć w jednym zdaniu – „Szukanie elementu minimalnego i przenoszenie go na początek”. Przejdźmy jednak do nieco bardziej szczegółowego opisu.
Algorytm rozpoczynamy, chcąc umieścić element minimalny całej tablicy, na samym jej początku. Przechodzimy więc przez całą tablicę, szukając go. Gdy już go odnajdziemy, zamieniamy go miejscami z elementem znajdującym się na zerowej pozycji. Wiemy już, że najmniejszy z elementów w naszym zbiorze, znajduje się na początku, więc zerowym miejscem w tablicy nie musimy się już przejmować.
Następny krok poszukiwania elementu minimalnego, zaczniemy więc nie od zerowej, a od pierwszej pozycji w tablicy, gdzie umieścimy kolejny minimalny element z rozpatrywanego podzbioru. Algorytm wykonujemy do momentu, gdy w kolejnej iteracji zaczynamy poszukiwanie minimalnego elementu na ostatniej pozycji tablicy. Otrzymujemy w ten sposób posortowany rosnąco zbiór.
W celu wizualizacji tego algorytmu, spójrzcie na poniższą animację:
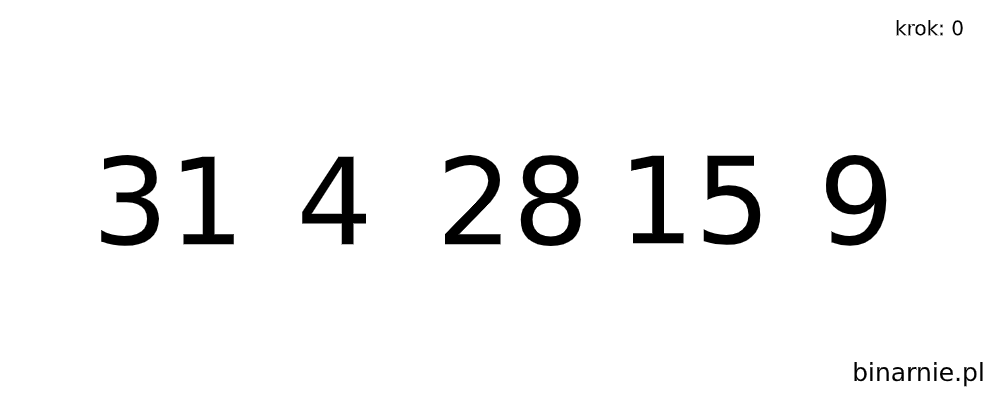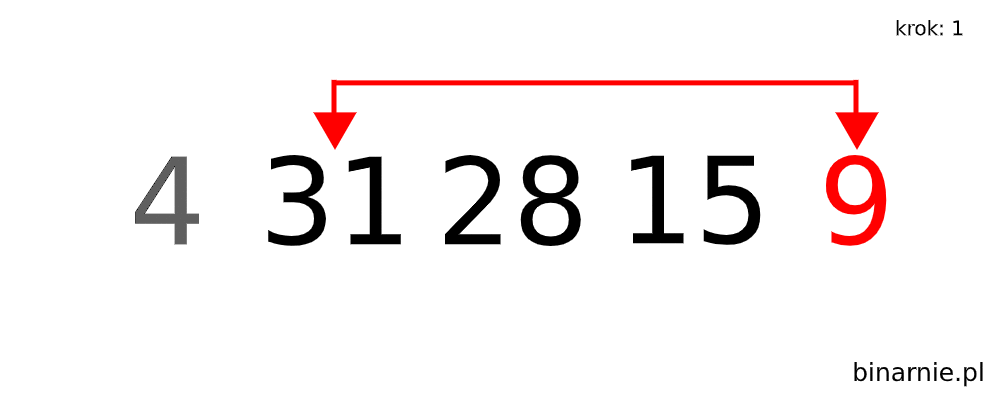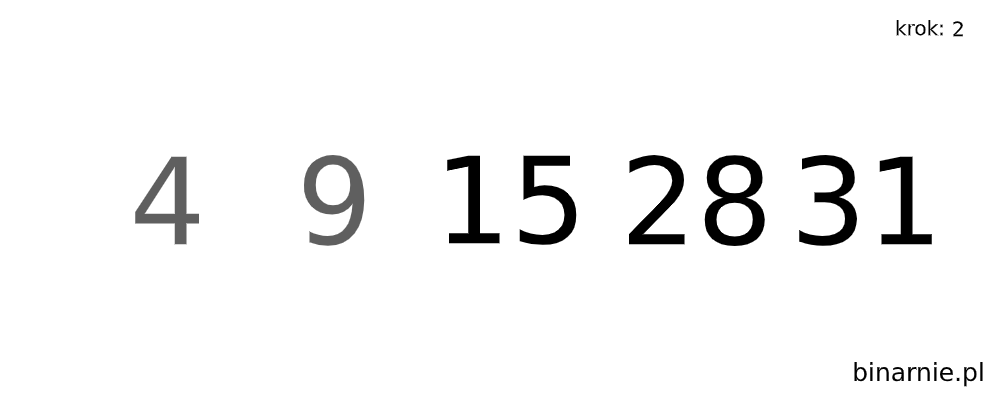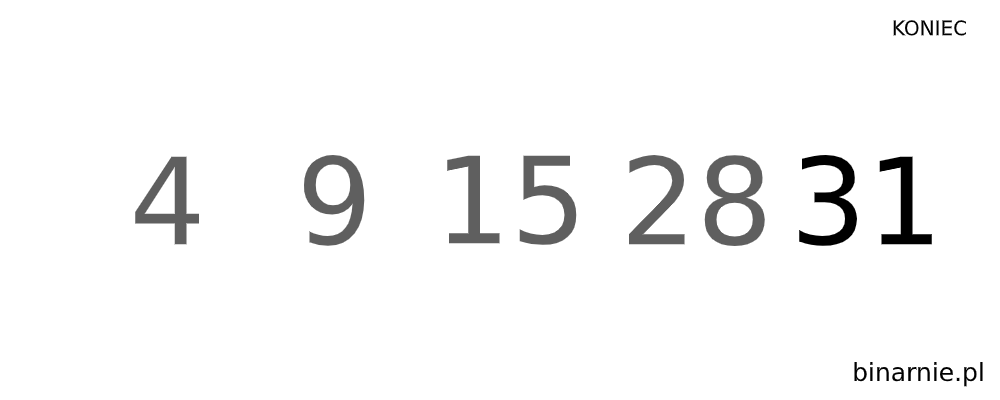
Sortowanie przez wybór -Implementacje
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 |
//program do sortowania n-elementowej tablicy //przy pomocy algorytmu sortowania przez wybór //Jan Żwirek #include <iostream> #include <algorithm> using namespace std; void printTab(int *tab, int n); void selectionSort(int *tab, int n) { int minElementPosition; for (int x = 0; x < n - 1; x++) { minElementPosition = x; for (int y = x + 1; y < n; y++) { //Sprawdzamy czy aktualnie wskazywanny element nie jest mniejszy, //od tego na pozycji minElementPosition if (tab[y] < tab[minElementPosition]) { minElementPosition = y; } } //Zamieniamy umiejscowienie elementu z pozycji minElementPosition, //tylko gdy jest na innej pozycji, niż oczekiwana if (x != minElementPosition) { cout << "\nKrok " << x << ": Wstawianie elementu minimalnego: " << tab[minElementPosition] << " na pozycje: " << x << endl; swap(tab[minElementPosition], tab[x]); printTab(tab, n); } } } int main() { int n; cout << "Wprowadz liczbe elementow tablicy: "; cin >> n; //Dynamiczne tworzenie tablicy int *tab = new int[n]; cout << "\nWprowadz " << n << " liczb do posortowania."; cout << "Zatwierdz kazda z nich klawiszem Enter:" << endl; for (int x = 0; x < n; x++) { cin >> tab[x]; } cout << endl << "Tablica przed posortowaniem:" << endl; printTab(tab, n); cout << endl << "Rozpoczecie sortowania" << endl; selectionSort(tab, n); cout << endl << "Oto tablica po sortowaniu:" << endl; for (int i = 0; i < n; i++) { cout << tab[i] << " "; } delete[] tab; system("pause"); return 0; } void printTab(int *tab, int n) { cout << endl; for (int x = 0; x < n; x++) { cout << tab[x] << " | "; } cout << endl; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
package matura; import java.util.Scanner; public class Main { private static void printArray(int[] tab) { System.out.println(); for(int i = 0; i < tab.length; i++) { System.out.print(tab[i] + " | "); } System.out.println(); } private static void selectionSort(int[] tab) { int minElementPosition; for (int x = 0; x < tab.length - 1; x++) { minElementPosition = x; for (int y = x + 1; y < tab.length; y++) { //Sprawdzamy czy aktualnie wskazywanny element nie jest mniejszy, //od tego na pozycji minElementPosition if (tab[y] < tab[minElementPosition]) { minElementPosition = y; } } //Zamieniamy umiejscowienie elementu z pozycji minElementPosition, //tylko gdy jest na innej pozycji, niż oczekiwana if (x != minElementPosition) { System.out.println("Krok " + x + ": Wstawianie elementu minimalnego: " + tab[minElementPosition] + " na pozycje: " + x); int pom = tab[x]; tab[x] = tab[minElementPosition]; tab[minElementPosition] = pom; printArray(tab); } } } public static void main(String[] args){ Scanner sc = new Scanner(System.in); //inicjalizujemy Scanner - obiekt pozwalajacy na wczytywanie zmiennych od uzytkownika System.out.println("Wprowadz liczbe elementow tablicy: "); int n = sc.nextInt(); int[] arr = new int[n]; for(int i = 1; i <= n; i++) { System.out.println("Podaj element nr." + i + ": "); arr[i-1]= sc.nextInt(); //wczytujemy kolejne elementy tablicy } System.out.println("Oto wprowadzona tablica:"); printArray(arr); selectionSort(arr); System.out.println("Oto wprowadzona tablica po przesortowaniu:"); printArray(arr); sc.close(); //zwalniamy zasoby } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
def wypisz(tab): #tworzymy metode do wypiswania zawartosci naszej tablicy for el in tab: print(el, end=" | ") def sortuj_wybor(tab, n): for x in range(n-1): #iterujemy poprzez wszsytkei elementy tablicy, poza ostatnim minimum = x #usatwiamy aktualny element jako ten najmniejszy for j in range(x+1, n): #a nastepnie szukamy elementow od niego mniejszych if tab[j] < tab[minimum]: minimum = j if x != minimum: #jezeli znajdziemy element jakkolwiek mniejszy print ("\nKrok ", (x+1), ": wstawianie elementu minimalnego ", tab[minimum], " na pozycje ", x) pom = tab[x] #dokonujemy jego zamiany tab[x] = tab[minimum] tab[minimum] = pom print("Podaj ilosc elementow tablicy:") a = int(input()) tablica = [] for i in range(a): print("Podaj element nr. ", (i+1)) tablica.append(int(input())) print("Oto twoja tablica:") wypisz(tablica) sortuj_wybor(tablica, a) print("Oto twoja tablica po sortowaniu:") wypisz(tablica) |
Powyższe implementacje sortują tablicę rosnąco, nic nie stoi jednak na przeszkodzie, by wykorzystać powyższe kody do sortowania malejącego. By to zrobić należy jedynie zamienić warunek:
„if (tab[y] < tab[minElementPosition])”
w funkcji sortującej, na:
„if (tab[y] > tab[maxElementPosition])”
oraz zmienić nazwę zminnej
minElementPosition, na maxElementPosition .

Nieco matematyki
Algorytm sortowania przez wybieranie wykonuje zawsze n-1 przejść przez tablicę, gdzie n jest liczbą elementów zbioru.
Posiada on złożoność czasową rzędu: O(n2). Wartość ta jest taka sama jak złożoność, znanego ze swej niskiej efektywności, sortowania bąbelkowego, którego opis i implementacje znajdziecie w poniższym wpisie. Algorytm ten nie jest więc polecany do sortowania dużych zbiorów liczb, ponieważ potrafi się nieco „zakrztusić”.
Podsumowanie
Warto znać algorytm sortowania przez wybieranie, ucząc się do matury z informatyki. Inne treści, dzięki którym przygotujesz się do niej, znajdziesz w zakładce „Matura z informatyki”.






msy
says:Warto zaznaczyć, że sortowanie przez wybór ma ZAWSZE złożoność dokładnie n(n-1)/2, gdzie n jest liczbą sortowanych elementów. Sortowanie bąbelkowe jest O(n^2), ale np. dla ciągu uporządkowanego ma złożoność liniową, dokładnie n-1 porównań.