W informatyce każdą informację możemy przedstawić na wiele sposobów. Przykładem może być prosta konwersja z typu całkowitego int na typ tekstowy string. Zabieg taki jest czasem wymagany, aby mieć łatwiejszą kontrolę nad programem lub, po prostu, aby wyświetlić użytkownikowi dane w odpowiedniej formie. Zamiana sposobu zapisu informacji jest również powszechnie wykorzystywana w procesie kompresji danych. Dzisiaj omówimy więc wspólnie jeden z ważniejszych algorytmów kompresji bezstratnej, jakim jest kodowanie Hoffmana.
Czym jest kompresja danych?
Krótko mówiąc kompresja danych ma na celu zminimalizowanie redundancji i tym samym zmniejszenie rozmiaru pliku.

Za przykład weźmy 12-elementowy zbiór. Łatwo zauważyć, że składa się on z 3 rodzajów figur geometrycznych. Z pozoru może wydawać się mało rozbudowany, jednak gdyby go powtórzyć 1000-krotnie mielibyśmy już 12000 elementów. Taką ilość elementów ciężej już sobie wyobrazić. Co można zrobić, by uprościć przedstawienie zbioru? Zamiast wypisywać tą samą figurę wielokrotnie pod rząd, wystarczy zapisać ją raz i dopisać ilość jej wystąpień. Powyższy zbiór możemy więc uprościć do:

W ten sposób zredukowaliśmy ilość elementów do sześciu i mimo, że nadal trudno by było sobie wyobrazić sześciotysięczny ciąg elementów, to jednak byłoby ich dwukrotnie mniej, niż przed „kompresją”. Podsumowując kompresją możemy nazwać proces, którego celem jest zredukowanie wielkości zbioru danych, poprzez zastępowanie powtarzających się ciągów prostszymi symbolami.
Algorytmy kompresji danych możemy podzielić na stratne i bezstratne. Kompresja bezstratna oznacza, że po dekompresji (procesie odwrotnym do kompresji) stan pliku będzie identyczny, jak przed kompresją. Stosowana jest np. w formatach GIF, PNG, czy wszędzie tam, gdzie ważne jest, aby każdy szczegół pliku był zachowany. Kodowanie Hoffmana, o którym będziemy dzisiaj mówić, jest przykładem kompresji bezstratnej.
Kompresja stratna oznacza, że po kompresji pewne szczegóły pliku są nieodwracalnie tracone i po dekompresji zostaną one pominięte. Kompresję stratną spotyka się np. w plikach JPEG, MP3, czy MPEG.
Kodowanie Huffmana – zasada działania
Kodowanie Huffmana polega na zastępowaniu złożonych partii danych pojedynczymi, prostymi kodami (ciągami bitów). W efekcie dane wyjściowe są znacznie krótsze od wejściowych.
By zrozumieć istotę kodowania Huffmana, przejdźmy do przykładu. Weźmy ciąg znaków „programowanie”. Jak pewnie dobrze wiecie, w klasycznym kodowaniu ASCII każdy znak reprezentowany jest przez jeden bajt danych, czyli 8 bitów. Za pomocą ośmiu bitów można zapisać 256 znaków. W powyższym słowie zapisanym w formacie ASCII nie wykorzystaliśmy jednak ich wszystkich, a mimo to zajęliśmy łącznie 13 bajtów. Nie potrzebujemy więc aż 256 znaków. Nasz ciąg składa się z liter z podanego zbioru : {p, r, o, g, a, m, w, n, i, e}. Wykorzystujemy więc jedynie 10 znaków z 256. Oznacza to, że na pojedynczy znak wystarczą nam 4 bity (24 = 16 > 10), zamiast ośmiu. Zauważ jednak, że im więcej liter wykorzystamy w tekście, tym mniej efektywny będzie ten algorytm. Gdyby wykorzystać w pliku wszystkie 256 znaków, to jego działanie nie miałoby żadnego efektu.
Kodowanie Huffmana – algorytm
Jak działa kodowanie Huffmana? W przypadku zbiorów znaków w pierwszej kolejności sprawdzana jest ilość wystąpień każdej litery ze zbioru, a następnie przypisywane jest im odpowiednia wartość. Znaki występujące najczęściej dostają najkrótsze kody, zaś te występujące rzadziej – dłuższe. W tym celu wykorzystuje się drzewo binarne, w które wpisywane są znaki i ich częstotliwości wystąpień. Jeżeli nie wiesz czym jest drzewo binarne, to odsyłam Cię do tego wpisu.
Działanie algorytmu możemy rozpisać następująco:
- Pobierz tekst od użytkownika;
- Zlicz ilość wystąpień dla każdego znaku;
- Dla każdego znaku utwórz liście drzewa binarnego; wartością liścia jest ilość wystąpień dla danego znaku
- Wybierz dwa liście o najmniejszych wartościach
- Utwórz nowy liść, który będzie kontenerem dla wybranych liści; jego wartość jest sumą ich wartości; mniejszy element będzie dzieckiem po lewo, większy dzieckiem po prawo
- Powtarzaj kroki 4-5, aż nie pozostanie jeden element – korzeń drzewa.
Na poniższej animacji prześledzisz działanie kodowania Huffmana, dla słowa „banany”:

Kodowanie Huffmana – implementacja C++ Java Python
Mając schemat działania pozostało nam już tylko wcielić go w życie 🙂 Zanim przejdziemy do faktycznego kodowania, musimy najpierw przygotować sobie odpowiednie obiekty i funkcje.
Na początek utwórzmy obiekt liścia – będzie on budulcem naszego drzewa. Musimy w nim zawrzeć jego wartość, wskaźniki na potomne liście oraz znak jaki reprezentuje. Dobrze jest również stworzyć przyjmujący wszystkie te wartości jako argumenty. Dzięki temu zaoszczędzimy sobie nieco wysiłku. Proponuję również dodać metodę typu logicznego, która zwróci, czy dany liść nie jest kontenerem dla innych liści.
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
//Tworzymy strukturę liścia, który będzie podstawowym budulcem drzewa kodowania. //Definiujemy w niej wskaźniki na lewe dziecko i prawe dziecko, //jej wartość(ilość wystąpień/ich sumę), znak do kodowania, a także zakodowany znak. struct Node{ Node *left; Node *right; char character; int value; Node(char c, int v, Node* l=nullptr, Node* r=nullptr){ //tworzymy konstruktor struktury left = l; right = r; character = c; value = v; } ~Node(){ //pamiętajmy, że zawsze powinno się wyczyścić wszelkie zmienne delete right; //dlatego zwalniamy pamięc zajętą przez dwójkę dzieci delete left; //z racji, iż jest to ten sam destruktor, funkcja ta wywoła się również u usuniętych dzieci } bool isLeaf(){ return character != '\0'; //tworzymy funkcję pomocniczą, która wskażę, czy jest to liść zawierający jakiś znak } }; |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
class Node { //tworzymy pomocniczą klasę, która przyda nam się przy tworzeniu drzewa binarnego private int value; //przechowywana wartość private Character character = null; //przechowywany znak public Node left = null; //lewe dziecko danego liścia public Node right = null; //prawe dziecko danego liścia public Node(char letter, int val) { //tworzymy konstruktor liścia dla znaków value = val; character = letter; } public Node(int val) { //tworzymy konstruktor dla liści będących sumą dzieci value = val; } public int getValue() { //funkcja zwracająca wartość liścia return value; } public Character getCharacter() {//funkcja zwracająca znak liścia return character; } public boolean isLeaf() { //funkcja zwracająca, czy liść nie jest kontenerem return character != null; } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
class Node: value = 0 right = None left = None character = "" def isLeaf(self): #pomocnicza metoda, która pozwoli określić, czy liść przechowuje znak return self.character != "" def __init__(self, val, ch): #definiujemy konstruktor self.value = val self.character = ch |
Gdy mamy już obiekt-liść, to musimy stworzyć kolejny obiekt, który będzie efektywnie te liście porównywać. Obiekt ten będzie miał znaczący wpływ na strukturę drzewa:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
//Tworzymy strukturę, która pomoże nam przy tworzeniu drzewa kodowania. //Będzie ona porównywać dwa liście z drzewa/ struct comparator{ bool operator() (Node *a, Node *b){ if(a->value != b->value) //jeżeli liście są różnej wartości return a->value > b->value; //wykonaj zwykłe porównanie if(!a->isLeaf() && b->isLeaf()) //jeżeli są równe i drugi jest kontenerem, to zawsze będzie on uznawany jako większy return false; if(!b->isLeaf() && a->isLeaf()) //jeżeli są równe i drugi jest kontenerem, to zawsze będzie on uznawany jako większy return true; if(a->isLeaf() && b->isLeaf()) //jeżeli oba są liściami return a->character > b->character; //to decyduje kolejność alfabetyczna return true; // jeżeli żaden z powyższych warunków nie zostanie spełniony, zwracamy true } }; |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
class NodeComparator implements Comparator < Node > { //tworzymy pomocniczą klasę, która przyda się przy porównywaniu liści drzewa; korzystamy z interfejsu Comparator @Override public int compare(Node n1, Node n2) { if(n1.getValue() != n2.getValue()) //jeżeli liście są różnej wartości return n1.getValue() - n2.getValue(); //wykonaj zwykłe porównanie if(n1.isLeaf() && !n2.isLeaf()) //jeżeli są równe i drugi jest kontenerem, to zawsze będzie on uznawany jako większy return 1; if(n2.isLeaf() && !n1.isLeaf()) //jeżeli są równe i drugi jest kontenerem, to zawsze będzie on uznawany jako większy return -1; if(n1.isLeaf() && n2.isLeaf()) //jeżeli oba są liściami return n1.getCharacter() - n2.getCharacter(); //to decyduje kolejność alfabetyczna return -1; // jeżeli żaden z powyższych warunków nie zostanie spełniony, zwracamy -1 - mniejszość } } |
Python
W Pythonie poniższą funkcję należy dodać do ciała klasy Node:
|
1 2 3 4 5 6 7 8 9 10 11 |
#funkcja __lt__ pomoże nam przy tworzeniu priority_queue def __lt__(self, other): if self.value != other.value: #wykonujemy normalne porównanie, jeżeli liście są różne; return self.value < other.value if not self.isLeaf() and other.isLeaf(): # w przeciwnym wypadku ważniejsze są liście mające znak return True if self.isLeaf() and not other.isLeaf(): # w przeciwnym wypadku ważniejsze są liście mające znak return False if self.isLeaf() and other.isLeaf(): #jeżeli jednak oba maja znak, to decyduje kolejność alfabetyczna return ord(self.character[0]) < ord(other.character[0]) return True |
Mając już potrzebne obiekty możemy przystąpić do tworzenia drzewa. Stworzymy więc funkcję o argumencie tekstowym, która zwróci obiekt Node będący korzeniem drzewa. Zanim jednak w ogóle zaczniemy je budować, musimy najpierw zliczyć znaki i stworzyć na ich podstawie liście drzewa. Utworzone liście dodamy do obiektu typu Priority Queue, który będzie porównywać je przy pomocy przygotowanej wyżej funkcji. Priority Queue jest obiektem o podobnej zasadzie działania, co stos, z tą róznicą, że dane nie zawsze są wrzucane na „wierzch”. Zamiast tego przy dodawaniu dokonuje się porównania i na podstawie jego wyniku element jest umieszczany na odpowiedniej pozycji.
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
//Definiujemy metodę, która stworzy drzewo kodowania Huffmana, a następnie zwróci jego korzeń //Argumentem jest tekst, który chcemy zakodować Node * createHuffmanTree(string line){ map<char, int> counter; //korzystamy z obiektu map, aby zliczyć wystąpienia dla każdego znaku for(char c : line){ if(counter.find(c) == counter.end()){ //jeżeli znaku nie ma w mapie counter[c] = 1; //dodajemy go } else{ counter[c]++; //jeżeli jest, zwiększamy jego ilość wystąpień } } //Tworzymy obiekt priority_queue, który będzie przechowywać nieprzypisane elementy drzewa. //Obiekt priority_queue pozwoli nam stworzyć uporządkowaną listę liści drzewa - najmniejsze będą najwyżej. //Do porównywania elementów wykorzystujemy wcześniej zdefiniowaną strukturę comparator. priority_queue<Node*, vector<Node*>, comparator> nodes; for(auto entry : counter){ nodes.push(new Node(entry.first, entry.second)); //tworzymy liście drzewa, bazując na znakach i ich ilości wystąpień } } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
private static Node createHuffmanTree(String line) { HashMap < Character, Integer > occurences = new HashMap < Character, Integer > (); //tworzymy mapę, która przechowa ilość wystąpień dla każdego znaku for (char c: line.toCharArray()) { //następnie zliczamy je w pętli if (occurences.containsKey(c)) { occurences.put(c, occurences.get(c) + 1); } else { occurences.put(c, 1); } } NodeComparator nc = new NodeComparator(); //tworzymy instancję pomocniczej klasy PriorityQueue < Node > nodes = new PriorityQueue < Node > (occurences.size(), nc); //korzystamy z PriorityQueue - w uproszczeniu jest to lista, która zadba, aby nasze elementy były zawsze posortowane; korzysta ona z naszego Comparatora for (Entry < Character, Integer > entry: occurences.entrySet()) { //zamieniamy znaki i ich ilość wystąpień na liście, a następnie dodajemy je do utworzonej listy Node n = new Node(entry.getKey(), entry.getValue()); nodes.add(n); } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
#Definiujemy metodę, która stworzy drzewo kodowania Huffmana, a następnie zwróci jego korzeń #Argumentem jest tekst, który chcemy zakodować def createTree(text): occurences = {} for c in text: #zliczamy wystąpienia każdego znaku w tekście if occurences.__contains__(c): occurences[c] += 1 else: occurences[c] = 1 # Tworzymy obiekt PriorityQueue(), który będzie przechowywać nieprzypisane elementy drzewa. # Obiekt priority_queue pozwoli nam stworzyć uporządkowaną listę liści drzewa - najmniejsze będą najwyżej. nodes = PriorityQueue() for c in occurences.keys(): #tworzymy liście drzewa, bazując na znakach i ich ilości wystąpień, a następnei dodajmy do listy node = Node(occurences[c], c) nodes.put(node) |
Następnie łączymy dwa liście o najmniejszej wartości, tworząc tym samym liść-kontener, którego wartością będzie suma wartości tych dwóch liści. Następnie dodajemy go do listy pozostałych liści. Kroki te powtarzamy, aż na liście nie zostanie jeden element – korzeń naszego drzewa. Wtedy to możemy zwrócić go jako wynik naszej funkcji – drzewo jest już wtedy zbudowane.
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
//Definiujemy metodę, która stworzy drzewo kodowania Huffmana, a następnie zwróci jego korzeń //Argumentem jest tekst, który chcemy zakodować Node * createHuffmanTree(string line){ map<char, int> counter; //korzystamy z obiektu map, aby zliczyć wystąpienia dla każdego znaku for(char c : line){ if(counter.find(c) == counter.end()){ //jeżeli znaku nie ma w mapie counter[c] = 1; //dodajemy go } else{ counter[c]++; //jeżeli jest, zwiększamy jego ilość wystąpień } } //Tworzymy obiekt priority_queue, który będzie przechowywać nieprzypisane elementy drzewa. //Obiekt priority_queue pozwoli nam stworzyć uporządkowaną listę liści drzewa - najmniejsze będą najwyżej. //Do porównywania elementów wykorzystujemy wcześniej zdefiniowaną strukturę comparator. priority_queue<Node*, vector<Node*>, comparator> nodes; for(auto entry : counter){ nodes.push(new Node(entry.first, entry.second)); //tworzymy liście drzewa, bazując na znakach i ich ilości wystąpień } Node *root; //definiujemy zmienną, która docelowo będzie korzeniem naszego drzewa while(nodes.size() > 1){ //następnie iterujemy, dopóki w nodes nie zostanie ostatni element - korzeń drzewa Node *n1 = nodes.top(); //pobieramy pierwszy, najmniejszy element z priority queue nodes.pop(); //a następnie go usuwamy Node *n2 = nodes.top(); //ponawiamy powyższe kroki, aby uzyskać drugi, najmniejszy element nodes.pop(); if(n1->value == n2->value && !n1->isLeaf()){ //jeżeli oba liście mają tą samą wartość, a jeden z nich jest kontenerem, to powinien on być traktowany jako większy element Node *pom = n1; //dlatego w takiej sytuacji podmieniamy wskaźniki n1 = n2; n2 = pom; } root = new Node('\0', n1->value + n2->value, n1, n2); //tworzymy liść-kontener, który będzie przechowywać dwa powyższe elementy i sumę ich wartości nodes.push(root); //a następnie dodajemy go do priority queue } return root; //gdy w priority queue zostanie tylko jeden wyraz, to oznacza, że drzewo zostało zbudowane, a wyraz ten jest jego korzeniem; zwracamy go } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
private static Node createHuffmanTree(String line) { HashMap < Character, Integer > occurences = new HashMap < Character, Integer > (); //tworzymy mapę, która przechowa ilość wystąpień dla każdego znaku for (char c: line.toCharArray()) { //następnie zliczamy je w pętli if (occurences.containsKey(c)) { occurences.put(c, occurences.get(c) + 1); } else { occurences.put(c, 1); } } NodeComparator nc = new NodeComparator(); //tworzymy instancję pomocniczej klasy PriorityQueue < Node > nodes = new PriorityQueue < Node > (occurences.size(), nc); //korzystamy z PriorityQueue - w uproszczeniu jest to lista, która zadba, aby nasze elementy były zawsze posortowane; korzysta ona z naszego Comparatora for (Entry < Character, Integer > entry: occurences.entrySet()) { //zamieniamy znaki i ich ilość wystąpień na liście, a następnie dodajemy je do utworzonej listy Node n = new Node(entry.getKey(), entry.getValue()); nodes.add(n); } Node rootNode = null; //zmienna pomocnicza przechowująca korzeń drzewa - finalnie ma być on liściem przechowującym wartość równą długości wpisanego wyrazu while (nodes.size() > 1) { //dopóki na liście nie pozostał jeden element(korzeń) Node n1 = nodes.peek(); //pobieramy najmniejszy element z listy nodes.poll(); //a następnie go usuwamy Node n2 = nodes.peek(); //ponownie pobieramy najmniejszy element z listy nodes.poll(); //i ponownie go usuwamy; w ten sposób pobraliśmy dwa najmniejsze elementy z listy Node parent = new Node(n1.getValue() + n2.getValue()); //tworzymy liść, który będzie przechowywał powyższe elementy if(n1.getValue() == n2.getValue() && !n1.isLeaf()) { /jeżeli oba liście mają tą samą wartość, a jeden z nich jest kontenerem, to powinien on być traktowany jako większy element Node pom = n1; //dlatego w takiej sytuacji podmieniamy wartości n1 = n2; n2 = pom; } rootNode = parent; // ustawiamy go tymczasowo jako korzeń parent.left = n1; // mniejszy element ustawamy jako jego lewe dziecko parent.right = n2;// większy jako jego prawe dziecko nodes.add(parent); //następnie dodajemy rodzica jako samodzielny element do listy } return rootNode; } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
#Definiujemy metodę, która stworzy drzewo kodowania Huffmana, a następnie zwróci jego korzeń #Argumentem jest tekst, który chcemy zakodować def createTree(text): occurences = {} for c in text: #zliczamy wystąpienia każdego znaku w tekście if occurences.__contains__(c): occurences[c] += 1 else: occurences[c] = 1 # Tworzymy obiekt PriorityQueue(), który będzie przechowywać nieprzypisane elementy drzewa. # Obiekt priority_queue pozwoli nam stworzyć uporządkowaną listę liści drzewa - najmniejsze będą najwyżej. nodes = PriorityQueue() for c in occurences.keys(): #tworzymy liście drzewa, bazując na znakach i ich ilości wystąpień, a następnei dodajmy do listy node = Node(occurences[c], c) nodes.put(node) rootNode = None #tworzymy zmienna przechowujaca docelowo korzen drzewa while nodes.qsize() > 1: #następnie iterujemy, dopóki w nodes nie zostanie ostatni element - korzeń drzewa n1 = nodes.get() #pobieramy pierwszy, najmniejszy element z PriorityQueue n2 = nodes.get() #pobieramy kolejny, najmniejszy element z PriorityQueue #jeżeli oba liście mają tą samą wartość, a jeden z nich jest kontenerem, to powinien on być traktowany jako większy element if n1.value == n2.value and not n1.isLeaf(): pom = n1 #dlatego w takiej sytuacji podmieniamy wskaźniki n1 = n2 n2 = pom parent = Node(n1.value + n2.value, "") #tworzymy liść-kontener, który będzie przechowywać dwa powyższe elementy i sumę ich wartości rootNode = parent #ustawiamy go na aktualny korzen parent.left = n1 #i dodajemy mu dzieci parent.right = n2 nodes.put(parent) #a następnie dodajemy go do PriorityQueue return rootNode #nasze drzewo jest gotowe - zwracamy korzeń |
Mamy już utworzone nasze drzewo. Możemy teraz zakodować jego wartości i stworzyć tablicę kodowania. W tym celu stworzymy funkcję rekurencyjną, która wykona się dla wszystkich elementów po lewo i po prawo dla każdego elementu. Jeżeli natrafimy na koniec drzewa, przerywamy rekurencję. Jeżeli temat rekurencji nie jest Ci do końca znany, rzuć okiem na wpis, w którym go wytłumaczyliśmy.
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
//Tworzymy rekurencyjną funkcję, która zakoduje elementy zależnie od ich pozycji w drzewie. //Jako argumenty podajemy korzeń drzewa, tekst pomocniczy przy rekurencji, a także mapę kodowania void encodeNodes(Node *node, string val, map<char, string> *map) { if(node == nullptr){ //warunek STOP funkcji rekurencyjnej: return; //jeżeli trafimy na koniec drzewa, przerywamy działanie } if(node->isLeaf()){ //jeżeli jest to liść przechowujący znak cout << node->character << " : " + val << endl; //to drukujemy go i jego zakodowaną wartość map->insert({node->character, val}); //a następnie dodajemy obie wartości do mapy } encodeNodes(node->left, val + '0', map); //wywołujemy jeszcze raz funkcję dla lewej strony drzewa - rekurencja encodeNodes(node->right, val + '1', map); //wywołujemy jeszcze raz funkcję dla prawej strony drzewa - rekurencja } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 |
private static void encodeValues(Node node, String txt, HashMap < Character, String > encodedValues) { //tworzymy rekurencyjną funkcję, która nada liścią odpowiednie wartości if (node == null) { return; } if (node.getCharacter() != null) { //jeżeli liść posiada swój znak System.out.println(node.getCharacter() + ":" + txt); encodedValues.put(node.getCharacter(), txt); //dodajemy jego zakodowaną wartość do tablicy } encodeValues(node.left, txt + "0", encodedValues); //wywołujemy funkcję rekurencyjnie encodeValues(node.right,txt + "1", encodedValues); //dla obu dzieci; w ten sposób całemu drzewu zostanie przypisana wartość } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 |
#tworzymy funkcję, która zakoduje drzewo #jednocześnie zakoduje ona podany przez użytkownika tekst def encodeValues(n, str, txt): if n is None: #jeżeli trafimy na koniec drzewa return txt #przerywamy rekurencję if n.isLeaf(): #jeżeli przechowuje on znak print(n.character + " : " + str) #to drukujemy go wraz z zakodowaną wartością txt = txt.replace(n.character, str) #a następnie podmieniamy znak w tekście z zakodowaną wartościa txt = encodeValues(n.left, str + "0", txt) #wykonujemy te same działania dla lewej części drzewa - rekurencja txt = encodeValues(n.right, str + "1", txt) #wykonujemy te same działania dla prawej części drzewa - rekurencja return txt #na koniec zwracamy zakodowany tekst |
Na sam koniec pozostało nam już tylko zakodowanie tekstu, przy użyciu utworzonej tablicy kodowania:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
int main(){ //pobieramy najpierw tekst od użytkownika cout << "Kodowanie Huffmana. Podaj tekst, który chcesz zakodować:" << endl; string line; getline(cin, line); //tworzymy drzewo bazując na tekście Node *root = createHuffmanTree(line); //kodujemy wartości w drzewie, drukujemy je i dodajemy do nowej mapy, która powiąże znaki z ich zakodowanymi wartościami cout<< "Oto tablica kodowania Huffmana:" << endl; map<char, string> encodedValues; encodeNodes(root, "", &encodedValues); //kodujemy tekst, bazując na utworzonej mapie kodowania string encodedLine = ""; for(char c : line){ encodedLine += encodedValues[c]; } cout << "Oto twoj tekst po zakodowaniu: " << encodedLine << endl; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
public static void main(String[] args) { System.out.println("Kodowanie Huffmana. Podaj tekst, który chcesz zakodować:"); Scanner sc = new Scanner(System.in); String line = sc.nextLine(); //pobieramy wiersz od użytkownika sc.close(); //pamiętając o zwalnianiu zasobów Node rootNode = createHuffmanTree(line); HashMap < Character, String > encodedValues = new HashMap < Character, String > (); //inicjalizujemy mapę, która przechowa tablicę kodowania System.out.println("Oto tablica kodowania:"); encodeValues(rootNode, "", encodedValues); //przypisujemy odpowiednie wartości gałęziom i liściom String output = ""; for (char c: line.toCharArray()) { output += encodedValues.get(c); //następnie kodujemy wyraz, korzystając z utworzonej tablicy kodowania } System.out.println(); System.out.println("Oto twój tekst zakodowany metodą Huffmana: " + output); } |
Python
|
1 2 3 4 5 |
word = input("Kodowanie Huffmana. Podaj tekst, który chcesz zakodować:").rstrip() rootNode = createTree(word) print("Oto tablica kodowania:") word = encodeValues(rootNode, "", word) print ("Oto tekst po zakodowaniu: " + word) |
Kodowanie Huffmana – odkodowanie
Powyższa procedura kodowania jest całkowicie odwracalna, o ile nadal mamy dostęp do drzewa lub tablicy kodowania. W pierwszym przypadku procedura jest prosta. Iterujemy poprzez każdy bit w kodzie. Jeżeli natrafimy na zero, idziemy w lewą stronę drzewa, jeżeli natomiast trafimy na jeden – wybieramy prawy liść. Gdy posiada on swój znak, to wstawiamy go w zmienną pomocniczą i wracamy na początek drzewa. Jeżeli jednak jest to kontener, to idziemy dalej, dopóki nie trafimy na liść zawierający znak. Czynności te powtarzamy do samego końca zakodowanego tekstu. W ich wyniku w zmiennej pomocniczej będzie znajdować się odkodowany tekst.
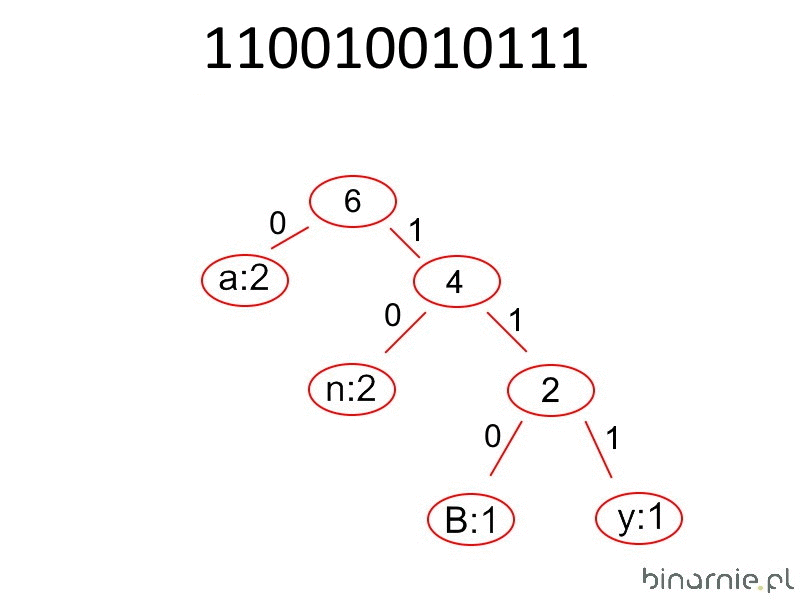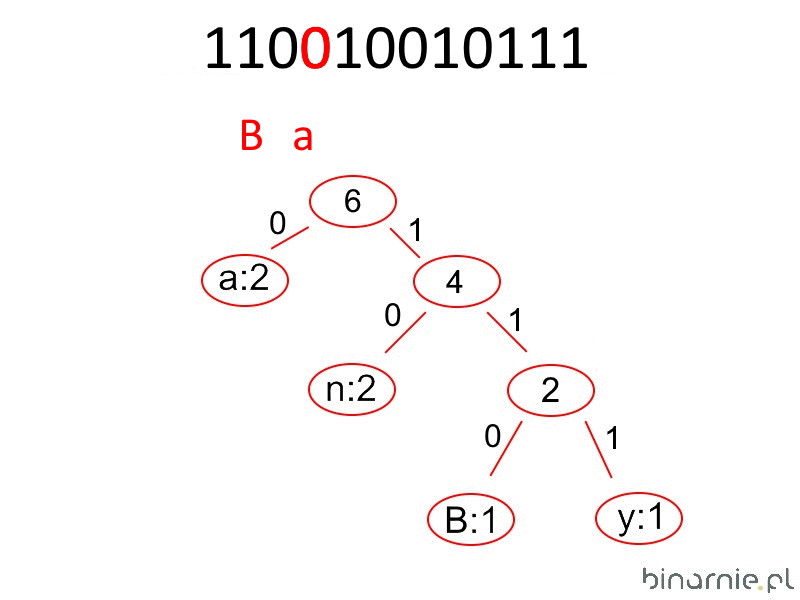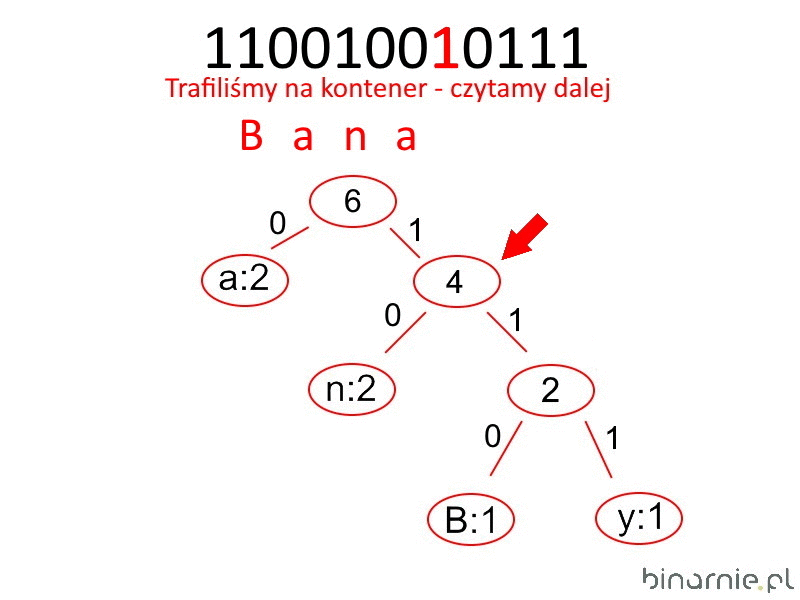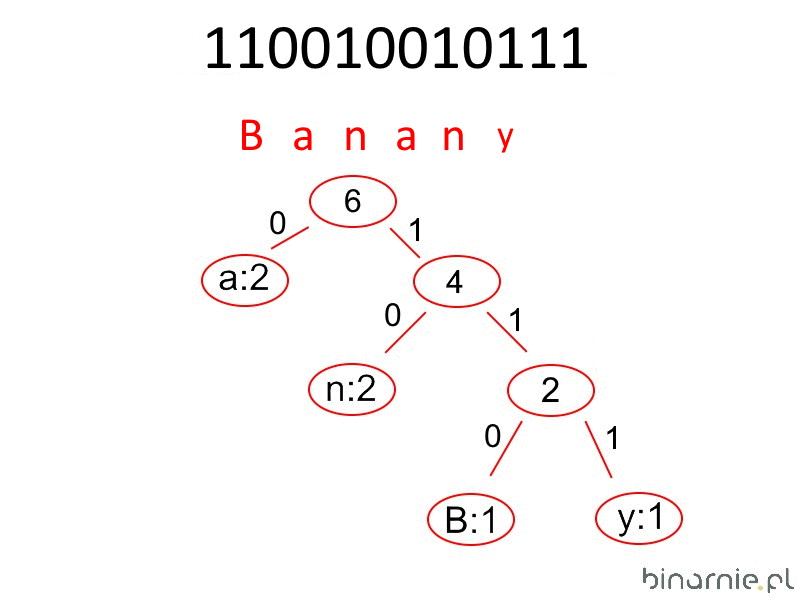
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
//Tworzymy funkcję, która odkoduje zakodowany tekst bazując na zbudowanym drzewie. string decode(Node *root, string encoded){ string decoded = ""; //zmienna pomocnicza Node *currentNode = root; //wskaźnik na aktualnie sprawdzany liść for(char c : encoded){ //iterujemy poprzez zakodowany tekst if(c == '0'){ //jeżeli iterowany znak jest zerem, to oznacza, że musimy iść w lewo if(currentNode->left->isLeaf()){ //jeżeli dziecko po lewo jest liściem przechowującym znak decoded += currentNode->left->character; //dodajemy ten znak do zmiennej pomocniczej currentNode = root; //a następnie wracamy na początek drzewa } else{ currentNode = currentNode->left; //jeżeli trafiliśmy na kontener, ustawiamy na niego wskaźnik } } else{ //jeżeli jest to inny znak (1), to przechodzimy na prawą stronę if(currentNode->right->isLeaf()){ //jeżeli dziecko po prawo jest liściem przechowującym znak decoded += currentNode->right->character;//dodajemy ten znak do zmiennej pomocniczej currentNode = root;//a następnie wracamy na początek drzewa } else{ currentNode = currentNode->right;//jeżeli trafiliśmy na kontener, ustawiamy na niego wskaźnik } } } return decoded; //na koniec zwracamy odkodowany tekst } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
private static String decode(Node root, String encoded){ String decoded = ""; //zmienna pomocnicza Node currentNode = root; //aktualnie sprawdzany liść for(char c : encoded.toCharArray()){ //iterujemy poprzez zakodowany tekst if(c == '0'){ //jeżeli iterowany znak jest zerem, to oznacza, że musimy iść w lewo if(currentNode.left.isLeaf()){ //jeżeli dziecko po lewo jest liściem przechowującym znak decoded += currentNode.left.getCharacter(); //dodajemy ten znak do zmiennej pomocniczej currentNode = root; //a następnie wracamy na początek drzewa } else{ currentNode = currentNode.left; //jeżeli trafiliśmy na kontener, ustawiamy go jako aktualny } } else{ //jeżeli jest to inny znak (1), to przechodzimy na prawą stronę if(currentNode.right.isLeaf()){ //jeżeli dziecko po prawo jest liściem przechowującym znak decoded += currentNode.right.getCharacter();//dodajemy ten znak do zmiennej pomocniczej currentNode = root;//a następnie wracamy na początek drzewa } else{ currentNode = currentNode.right;//jeżeli trafiliśmy na kontener, ustawiamy go jako aktualny } } } return decoded; //na koniec zwracamy odkodowany tekst } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
#definiujemy funkcję, która odkoduje tekst na bazie utworzonego drzewa def decode(root, text): decoded = "" #zmienna pomocnicza currNode = root #aktualnie rozważany element drzewa for char in text: #iterujemy poprzez znaki zakodowanego tekstu if char == '0': #jeżeli jest to 0, to oznacza, że musimy iśc na lewą stronę if currNode.left.isLeaf(): #jeżeli element po lewo jest liściem decoded += currNode.left.character #to dodajemy jego znak do zmiennej pomocniczej currNode = root #a następnie wracamy na początek drzewa else: currNode = currNode.left #jeżeli trafiliśmy na kontener, to od niego zaczniemy nast. iterację else: #jeżeli jest to 1, to oznacza, że musimy iśc na prawą stronę if currNode.right.isLeaf(): #jeżeli element po prawo jest liściem decoded += currNode.right.character #to dodajemy jego znak do zmiennej pomocniczej currNode = root #a następnie wracamy na początek drzewa else: currNode = currNode.right #jeżeli trafiliśmy na kontener, to od niego zaczniemy nast. iterację return decoded #zwracamy odkodowana wartosc |

Podsumowanie
W ten oto sposób udało nam się wspólnie zaimplementować kodowanie Huffmana. Z racji na swoją niską wydajność, praktycznie wcale nie korzysta się z niego samodzielnie. Wykorzystywany jest on jednak jako ostatni etap kompresji, najczęściej w połączeniu z kilkoma innymi metodami. Niemniej jednak jest to algorytm warty poznania i zrozumienia. Kto wie, może spotkacie się z nim na maturze? Poniżej znajdziecie pełną implementację kodowania Huffmana:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 |
#include <iostream> #include <queue> #include <string> #include <map> #include <vector> #include <algorithm> using namespace std; //Tworzymy strukturę liścia, który będzie podstawowym budulcem drzewa kodowania. //Definiujemy w niej wskaźniki na lewe dziecko i prawe dziecko, //jej wartość(ilość wystąpień/ich sumę), znak do kodowania, a także zakodowany znak. struct Node{ Node *left; Node *right; char character; int value; Node(char c, int v, Node* l=nullptr, Node* r=nullptr){ //tworzymy konstruktor struktury left = l; right = r; character = c; value = v; } ~Node(){ //pamiętajmy, że zawsze powinno się wyczyścić wszelkie zmienne delete right; //dlatego zwalniamy pamięc zajętą przez dwójkę dzieci delete left; //z racji, iż jest to destruktor, funkcja ta wywoła się również u usuniętych dzieci } bool isLeaf(){ return character != '\0'; //tworzymy funkcję pomocniczą, która wskażę, czy jest to liść zawierający jakiś znak } }; //Tworzymy strukturę, która pomoże nam przy tworzeniu drzewa kodowania. //Będzie ona porównywać dwa liście z drzewa/ struct comparator{ bool operator() (Node *a, Node *b){ if(a->value != b->value) //jeżeli liście są różnej wartości return a->value > b->value; //wykonaj zwykłe porównanie if(!a->isLeaf() && b->isLeaf()) //jeżeli są równe i drugi jest kontenerem, to zawsze będzie on uznawany jako większy return false; if(!b->isLeaf() && a->isLeaf()) //jeżeli są równe i drugi jest kontenerem, to zawsze będzie on uznawany jako większy return true; if(a->isLeaf() && b->isLeaf()) //jeżeli oba są liściami return a->character > b->character; //to decyduje kolejność alfabetyczna return true; // jeżeli żaden z powyższych warunków nie zostanie spełniony, zwracamy true } }; //Definiujemy metodę, która stworzy drzewo kodowania Huffmana, a następnie zwróci jego korzeń //Argumentem jest tekst, który chcemy zakodować Node * createHuffmanTree(string line){ map<char, int> counter; //korzystamy z obiektu map, aby zliczyć wystąpienia dla każdego znaku for(char c : line){ if(counter.find(c) == counter.end()){ //jeżeli znaku nie ma w mapie counter[c] = 1; //dodajemy go } else{ counter[c]++; //jeżeli jest, zwiększamy jego ilość wystąpień } } //Tworzymy obiekt priority_queue, który będzie przechowywać nieprzypisane elementy drzewa. //Obiekt priority_queue pozwoli nam stworzyć uporządkowaną listę liści drzewa - najmniejsze będą najwyżej. //Do porównywania elementów wykorzystujemy wcześniej zdefiniowaną strukturę comparator. priority_queue<Node*, vector<Node*>, comparator> nodes; for(auto entry : counter){ nodes.push(new Node(entry.first, entry.second)); //tworzymy liście drzewa, bazując na znakach i ich ilości wystąpień } Node *root; //definiujemy zmienną, która docelowo będzie korzeniem naszego drzewa while(nodes.size() > 1){ //następnie iterujemy, dopóki w nodes nie zostanie ostatni element - korzeń drzewa Node *n1 = nodes.top(); //pobieramy pierwszy, najmniejszy element z priority queue nodes.pop(); //a następnie go usuwamy Node *n2 = nodes.top(); //ponawiamy powyższe kroki, aby uzyskać drugi, najmniejszy element nodes.pop(); if(n1->value == n2->value && !n1->isLeaf()){ //jeżeli oba liście mają tą samą wartość, a jeden z nich jest kontenerem, to powinien on być traktowany jako większy element Node *pom = n1; //dlatego w takiej sytuacji podmieniamy wskaźniki n1 = n2; n2 = pom; } root = new Node('\0', n1->value + n2->value, n1, n2); //tworzymy liść-kontener, który będzie przechowywać dwa powyższe elementy i sumę ich wartości nodes.push(root); //a następnie dodajemy go do priority queue } return root; //gdy w priority queue zostanie tylko jeden wyraz, to oznacza, że drzewo zostało zbudowane, a wyraz ten jest jego korzeniem; zwracamy go } //Tworzymy rekurencyjną funkcję, która zakoduje elementy zależnie od ich pozycji w drzewie. //Jako argumenty podajemy korzeń drzewa, tekst pomocniczy przy rekurencji, a także mapę kodowania void encodeNodes(Node *node, string val, map<char, string> *map) { if(node == nullptr){ //warunek STOP funkcji rekurencyjnej: return; //jeżeli trafimy na koniec drzewa, przerywamy działanie } if(node->isLeaf()){ //jeżeli jest to liść przechowujący znak cout << node->character << " : " + val << endl; //to drukujemy go i jego zakodowaną wartość map->insert({node->character, val}); //a następnie dodajemy obie wartości do mapy } encodeNodes(node->left, val + '0', map); //wywołujemy jeszcze raz funkcję dla lewej strony drzewa - rekurencja encodeNodes(node->right, val + '1', map); //wywołujemy jeszcze raz funkcję dla prawej strony drzewa - rekurencja } //Tworzymy funkcję, która odkoduje zakodowany tekst bazując na zbudowanym drzewie. string decode(Node *root, string encoded){ string decoded = ""; //zmienna pomocnicza Node *currentNode = root; //wskaźnik na aktualnie sprawdzany liść for(char c : encoded){ //iterujemy poprzez zakodowany tekst if(c == '0'){ //jeżeli iterowany znak jest zerem, to oznacza, że musimy iść w lewo if(currentNode->left->isLeaf()){ //jeżeli dziecko po lewo jest liściem przechowującym znak decoded += currentNode->left->character; //dodajemy ten znak do zmiennej pomocniczej currentNode = root; //a następnie wracamy na początek drzewa } else{ currentNode = currentNode->left; //jeżeli trafiliśmy na kontener, ustawiamy na niego wskaźnik } } else{ //jeżeli jest to inny znak (1), to przechodzimy na prawą stronę if(currentNode->right->isLeaf()){ //jeżeli dziecko po prawo jest liściem przechowującym znak decoded += currentNode->right->character;//dodajemy ten znak do zmiennej pomocniczej currentNode = root;//a następnie wracamy na początek drzewa } else{ currentNode = currentNode->right;//jeżeli trafiliśmy na kontener, ustawiamy na niego wskaźnik } } } return decoded; //na koniec zwracamy odkodowany tekst } int main(){ //pobieramy najpierw tekst od użytkownika cout << "Kodowanie Huffmana. Podaj tekst, który chcesz zakodować:" << endl; string line; getline(cin, line); //tworzymy drzewo bazując na tekście Node *root = createHuffmanTree(line); //kodujemy wartości w drzewie, drukujemy je i dodajemy do nowej mapy, która powiąże znaki z ich zakodowanymi wartościami cout<< "Oto tablica kodowania Huffmana:" << endl; map<char, string> encodedValues; encodeNodes(root, "", &encodedValues); //kodujemy tekst, bazując na utworzonej mapie kodowania string encodedLine = ""; for(char c : line){ encodedLine += encodedValues[c]; } cout << "Oto twoj tekst po zakodowaniu: " << encodedLine << endl; //odkodowujemy tekst, aby sprawdzić działanie cout << "Oto tekst po odkodowaniu: " << decode(root, encodedLine) << endl; //sprzątamy po sobie :) delete root; return 0; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 |
package matura; import java.util.Comparator; import java.util.HashMap; import java.util.Map.Entry; import java.util.PriorityQueue; import java.util.Scanner; class Node { //tworzymy kolejną, pomocniczą klasę, która przyda nam się przy tworzeniu drzewa binarnego private int value; //przechowywana wartość private Character character = null; //przechowywany znak public Node left = null; //lewe dziecko danego liścia public Node right = null; //prawe dziecko danego liścia public Node(char letter, int val) { //tworzymy konstruktor liścia dla znaków value = val; character = letter; } public Node(int val) { //tworzymy konstruktor liścia dla liści będących sumą dzieci value = val; } public int getValue() { //funkcja zwracająca wartość liścia return value; } public Character getCharacter() {//funkcja zwracająca znak liścia return character; } public boolean isLeaf() { return character != null; } } class NodeComparator implements Comparator < Node > { //tworzymy pomocniczą klasę, która przyda się przy porównywaniu liści drzewa; korzystamy z interfejsu Comparator @Override public int compare(Node n1, Node n2) { if(n1.getValue() != n2.getValue()) //jeżeli liście są różnej wartości return n1.getValue() - n2.getValue(); //wykonaj zwykłe porównanie if(n1.isLeaf() && !n2.isLeaf()) //jeżeli są równe i drugi jest kontenerem, to zawsze będzie on uznawany jako większy return 1; if(n2.isLeaf() && !n1.isLeaf()) //jeżeli są równe i drugi jest kontenerem, to zawsze będzie on uznawany jako większy return -1; if(n1.isLeaf() && n2.isLeaf()) //jeżeli oba są liściami return n1.getCharacter() - n2.getCharacter(); //to decyduje kolejność alfabetyczna return -1; // jeżeli żaden z powyższych warunków nie zostanie spełniony, zwracamy -1 - mniejszość } } public class Kodowanie_Huffman { private static Node createHuffmanTree(String line) { HashMap < Character, Integer > occurences = new HashMap < Character, Integer > (); //tworzymy mapę, która przechowa ilość wystąpień dla każdego znaku for (char c: line.toCharArray()) { //następnie zliczamy je w pętli if (occurences.containsKey(c)) { occurences.put(c, occurences.get(c) + 1); } else { occurences.put(c, 1); } } NodeComparator nc = new NodeComparator(); //tworzymy instancję pomocniczej klasy PriorityQueue < Node > nodes = new PriorityQueue < Node > (occurences.size(), nc); //korzystamy z PriorityQueue - w uproszczeniu jest to lista, która zadba, aby nasze elementy były zawsze posortowane; korzysta ona z naszego Comparatora for (Entry < Character, Integer > entry: occurences.entrySet()) { //zamieniamy znaki i ich ilość wystąpień na liście, a następnie dodajemy je do utworzonej listy Node n = new Node(entry.getKey(), entry.getValue()); nodes.add(n); } Node rootNode = null; //zmienna pomocnicza przechowująca korzeń drzewa - finalnie ma być on liściem przechowującym wartość równą długości wpisanego wyrazu while (nodes.size() > 1) { //dopóki na liście nie pozostał jeden element(korzeń) Node n1 = nodes.peek(); //pobieramy najmniejszy element z listy nodes.poll(); //a następnie go usuwamy Node n2 = nodes.peek(); //ponownie pobieramy najmniejszy element z listy nodes.poll(); //i ponownie go usuwamy; w ten sposób pobraliśmy dwa najmniejsze elementy z listy Node parent = new Node(n1.getValue() + n2.getValue()); //tworzymy liść, który będzie przechowywał powyższe elementy if(n1.getValue() == n2.getValue() && !n1.isLeaf()) { Node pom = n1; n1 = n2; n2 = pom; } rootNode = parent; // ustawiamy go tymczasowo jako korzeń parent.left = n1; // mniejszy element ustawamy jako jego lewe dziecko parent.right = n2;// większy jako jego prawe dziecko nodes.add(parent); //następnie dodajemy rodzica jako samodzielny element do listy } return rootNode; } private static void encodeValues(Node node, String txt, HashMap < Character, String > encodedValues) { //tworzymy rekurencyjną funkcję, która nada liścią odpowiednie wartości if (node == null) { return; } if (node.getCharacter() != null) { //jeżeli liść posiada swój znak System.out.println(node.getCharacter() + ":" + txt); encodedValues.put(node.getCharacter(), txt); //dodajemy jego zakodowaną wartość do tablicy } encodeValues(node.left, txt + "0", encodedValues); //wywołujemy funkcję rekurencyjnie encodeValues(node.right,txt + "1", encodedValues); //dla obu dzieci; w ten sposób całemu drzewu zostanie przypisana wartość } private static String decode(Node root, String encoded){ String decoded = ""; //zmienna pomocnicza Node currentNode = root; //aktualnie sprawdzany liść for(char c : encoded.toCharArray()){ //iterujemy poprzez zakodowany tekst if(c == '0'){ //jeżeli iterowany znak jest zerem, to oznacza, że musimy iść w lewo if(currentNode.left.isLeaf()){ //jeżeli dziecko po lewo jest liściem przechowującym znak decoded += currentNode.left.getCharacter(); //dodajemy ten znak do zmiennej pomocniczej currentNode = root; //a następnie wracamy na początek drzewa } else{ currentNode = currentNode.left; //jeżeli trafiliśmy na kontener, ustawiamy go jako aktualny } } else{ //jeżeli jest to inny znak (1), to przechodzimy na prawą stronę if(currentNode.right.isLeaf()){ //jeżeli dziecko po prawo jest liściem przechowującym znak decoded += currentNode.right.getCharacter();//dodajemy ten znak do zmiennej pomocniczej currentNode = root;//a następnie wracamy na początek drzewa } else{ currentNode = currentNode.right;//jeżeli trafiliśmy na kontener, ustawiamy go jako aktualny } } } return decoded; //na koniec zwracamy odkodowany tekst } public static void main(String[] args) { System.out.println("Kodowanie Huffmana. Podaj tekst, który chcesz zakodować:"); Scanner sc = new Scanner(System.in); String line = sc.nextLine(); //pobieramy wiersz od użytkownika sc.close(); //pamiętając o zwalnianiu zasobów Node rootNode = createHuffmanTree(line); HashMap < Character, String > encodedValues = new HashMap < Character, String > (); //inicjalizujemy mapę, która przechowa tablicę kodowania System.out.println("Oto tablica kodowania:"); encodeValues(rootNode, "", encodedValues); //przypisujemy odpowiednie wartości gałęziom i liściom String output = ""; for (char c: line.toCharArray()) { output += encodedValues.get(c); //następnie kodujemy wyraz, korzystając z utworzonej tablicy kodowania } System.out.println(); System.out.println("Oto twój tekst zakodowany metodą Huffmana: " + output); System.out.println(); System.out.println("Oto odkodowany tekst: " + decode(rootNode, output)); } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 |
from queue import PriorityQueue #importujemy PriorityQueue #tworzymy klasę Node, która będzie podstaowym budulcem drzewa kodowania #będzie ona przechowywać wartość, lewe i prawe dziecko, zakodowaną wartość, a także znak class Node: value = 0 right = None left = None character = "" def isLeaf(self): #pomocnicza metoda, która pozwoli określić, czy liść przechowuje znak return self.character != "" def __init__(self, val, ch): #definiujemy konstruktor self.value = val self.character = ch #funkcja __lt__ pomoże nam przy tworzeniu priority_queue def __lt__(self, other): if self.value != other.value: #wykonujemy normalne porównanie, jeżeli liście są różne; return self.value < other.value if not self.isLeaf() and other.isLeaf(): # w przeciwnym wypadku ważniejsze są liście mające znak return True if self.isLeaf() and not other.isLeaf(): # w przeciwnym wypadku ważniejsze są liście mające znak return False if self.isLeaf() and other.isLeaf(): #jeżeli jednak oba maja znak, to decyduje kolejność alfabetyczna return ord(self.character[0]) < ord(other.character[0]) return True #Definiujemy metodę, która stworzy drzewo kodowania Huffmana, a następnie zwróci jego korzeń #Argumentem jest tekst, który chcemy zakodować def createTree(text): occurences = {} for c in text: #zliczamy wystąpienia każdego znaku w tekście if occurences.__contains__(c): occurences[c] += 1 else: occurences[c] = 1 # Tworzymy obiekt PriorityQueue(), który będzie przechowywać nieprzypisane elementy drzewa. # Obiekt priority_queue pozwoli nam stworzyć uporządkowaną listę liści drzewa - najmniejsze będą najwyżej. nodes = PriorityQueue() for c in occurences.keys(): #tworzymy liście drzewa, bazując na znakach i ich ilości wystąpień, a następnei dodajmy do listy node = Node(occurences[c], c) nodes.put(node) rootNode = None #tworzymy zmienna przechowujaca docelowo korzen drzewa while nodes.qsize() > 1: #następnie iterujemy, dopóki w nodes nie zostanie ostatni element - korzeń drzewa n1 = nodes.get() #pobieramy pierwszy, najmniejszy element z PriorityQueue n2 = nodes.get() #pobieramy kolejny, najmniejszy element z PriorityQueue #jeżeli oba liście mają tą samą wartość, a jeden z nich jest kontenerem, to powinien on być traktowany jako większy element if n1.value == n2.value and not n1.isLeaf(): pom = n1 #dlatego w takiej sytuacji podmieniamy wskaźniki n1 = n2 n2 = pom parent = Node(n1.value + n2.value, "") #tworzymy liść-kontener, który będzie przechowywać dwa powyższe elementy i sumę ich wartości rootNode = parent #ustawiamy go na aktualny korzen parent.left = n1 #i dodajemy mu dzieci parent.right = n2 nodes.put(parent) #a następnie dodajemy go do PriorityQueue return rootNode #nasze drzewo jest gotowe - zwracamy korzeń #tworzymy funkcję, która zakoduje drzewo #jednocześnie zakoduje ona podany przez użytkownika tekst def encodeValues(n, str, txt): if n is None: #jeżeli trafimy na koniec drzewa return txt #przerywamy rekurencję if n.isLeaf(): #jeżeli przechowuje on znak print(n.character + " : " + str) #to drukujemy go wraz z zakodowaną wartością txt = txt.replace(n.character, str) #a następnie podmieniamy znak w tekście z zakodowaną wartościa txt = encodeValues(n.left, str + "0", txt) #wykonujemy te same działania dla lewej części drzewa - rekurencja txt = encodeValues(n.right, str + "1", txt) #wykonujemy te same działania dla prawej części drzewa - rekurencja return txt #na koniec zwracamy zakodowany tekst #definiujemy funkcję, która odkoduje tekst na bazie utworzonego drzewa def decode(root, text): decoded = "" #zmienna pomocnicza currNode = root #aktualnie rozważany element drzewa for char in text: #iterujemy poprzez znaki zakodowanego tekstu if char == '0': #jeżeli jest to 0, to oznacza, że musimy iśc na lewą stronę if currNode.left.isLeaf(): #jeżeli element po lewo jest liściem decoded += currNode.left.character #to dodajemy jego znak do zmiennej pomocniczej currNode = root #a następnie wracamy na początek drzewa else: currNode = currNode.left #jeżeli trafiliśmy na kontener, to od niego zaczniemy nast. iterację else: #jeżeli jest to 1, to oznacza, że musimy iśc na prawą stronę if currNode.right.isLeaf(): #jeżeli element po prawo jest liściem decoded += currNode.right.character #to dodajemy jego znak do zmiennej pomocniczej currNode = root #a następnie wracamy na początek drzewa else: currNode = currNode.right #jeżeli trafiliśmy na kontener, to od niego zaczniemy nast. iterację return decoded #zwracamy odkodowana wartosc word = input("Kodowanie Huffmana. Podaj tekst, który chcesz zakodować:").rstrip() rootNode = createTree(word) print("Oto tablica kodowania:") word = encodeValues(rootNode, "", word) print ("Oto tekst po zakodowaniu: " + word) word = decode(rootNode, word) print("Oto odkodowany tekst: " + word) |






Khasreto
says:Super artykuł 😉 Fajnie ze masz czas robić coś takiego.