Zaczyna się ulubiony dzień każdego z nas, a wraz z nim pojawia się kolejna część „Piątku z sortowaniem”. Tym razem weźmiemy pod lupę sortowanie binarne (binary sort), które jest sprawą odrobinę bardziej skomplikowaną, od wcześniej prezentowanych algorytmów. Nie bójcie się jednak. Razem przeanalizujemy jego działanie krok po kroku.

Poszukiwania

Zanim przejdziemy do algorytmu sortowania, musimy zadać sobie ważne pytanie. Jak ma się wyszukiwanie binarne do algorytmu sortowania binarnego?

Sortowanie binarne, jest tak naprawdę modyfikacją sortowania przez wstawianie. Jeśli jeszcze go nie znacie, jego opis oraz implementacje znajdziecie w poprzedniej części „Piątku z sortowaniem”. Algorytm ten został ulepszony przez dodanie wyszukiwania binarnego, więc ujmując rzecz precyzyjnie, sortowanie binarne, to tak naprawdę sortowanie przez wstawianie z wyszukiwaniem binarnym (binary insertion sort). Nic dziwnego, że potocznie przyjęto krótszą nazwę 😉.

By więc w pełni zrozumieć sortowanie binarne, najpierw musimy poznać jak dokładnie działa wyszukiwanie binarne.

Dziel i zwyciężaj

Algorytm wyszukiwania binarnego służy do wyszukiwania elementów w posortowanym zbiorze liczbowym. Opiera się on na, bardzo dobrze znanej w programowaniu, zasadzie „dziel i zwyciężaj”. Algorytm ten dzieli tablice na mniejsze części, aż do momentu znalezienia szukanego elementu. Omówmy jego działanie krok po kroku.

1.Na początku wyznaczamy środkową pozycję tablicy, korzystając z wzoru:

sr = (l + p)/2

gdzie:

• sr – indeks środka tablicy
• l – indeks lewego krańca tablicy
• p – indeks prawego krańca tablicy

Jeśli tablica ma parzystą liczbę elementów, to wynik dzielenia zaokrąglamy w dół. Zakładamy, że do obliczeń używamy liczb całkowitych (int), w przypadku których, reszta z dzielenia jest zwyczajnie odrzucana.

2.Gdy nasze zmienne są już wyznaczone, sprawdzamy czy liczba, kryjąca się pod indeksem sr, jest szukaną liczbą. Jeśli nie, sprawdzamy czy szukany element jest większy, czy mniejszy od elementu pod indeksem sr. Mamy wtedy dwa możliwe scenariusze:

• Element szukany jest większy – Jako, iż jest to posortowany zbiór, logicznym jest, że nasz element powinien znajdować się na prawo od środkowego indeksu, wśród większych liczb. Wyznaczamy więc podtablicę, odrzucając wszystkie elementy znajdujące się przed indeksem sr+1. Dokonujemy tego, przez zmianę wartości lewego indeksu tablicy:

l = sr + 1

• Element szukany jest mniejszy – Analogicznie do powyższej sytuacji, wyznaczamy podtablicę, odrzucając wszystkie elementy znajdujące się na prawo od indeksu sr-1:

p = sr -1

Ponownie wykonujemy wszystkie kroki, zaczynając od wyznaczenia środkowego indeksu sr. Robimy to, aż do momentu gdy natrafimy na szukany element.

Co jeśli szukanego elementu nie ma w zbiorze? Algorytm ten jest również przygotowany na tą możliwość. Przed każdym wyznaczeniem nowego indeksu sr, wystarczy sprawdzić czy l>r. Jeśli tak, oznacza to, że naszego elementu nie ma w zbiorze.

By zobrazować sobie działanie algorytmu spójrzcie na poniższą animację:

Zauważcie, że w powyższym przypadku, korzystając z wyszukiwania liniowego (przechodzenia przez wszystkie elementy po kolei), znalezienie indeksu szukanego elementu, zajęłoby nam aż pięć kroków. Korzystając z wyszukiwania binarnego, znaleźliśmy element w trzech. Łatwo wyobrazić sobie ile kroków „zaoszczędzilibyśmy”, w przypadku przeszukiwania, nie siedmioelementowego zbioru, lecz tablicy z siedmioma tysiącami elementów.

Znając już w pełni zasadę działa wyszukiwania binarnego, możemy przejść do sortowania binarnego.

Ulepszenie

Sortowanie binarne nie różni się znacząco, od omawianego w poprzedniej części, sortowania przez wstawianie. Nic dziwnego, skoro jest to jego usprawniona wersja. Tak samo jak w podstawowej wersji algorytmu, wybieramy kolejne elementy i wstawiamy je w miejsca docelowe. Jedyną różnicą jest fakt, że do wyszukania pozycji, w której ma znaleźć się wybrany przez nas element, skorzystamy z wyszukiwania binarnego.

Jak jednak wyznaczyć warunek końca algorytmu wyszukiwania binarnego, skoro wcześniej szukaliśmy konkretnego elementu, a nie dogodnej pozycji? Otóż jego działanie wyglądać będzie następująco.

Wybierając element, który mamy wstawić w miejsce docelowe, wyznaczamy środek już uporządkowanego zbioru liczb, gdzie indeksy l i r, są jego krańcami. Następnie porównujemy wybrany element, z elementem pod środkowym indeksem. Jeśli jest mniejszy – odrzucamy całą prawą część podtablicy. Jeśli będzie większy – odrzucamy lewą.

Są dwa główne warunki końca algorytmu wyszukiwania pozycji:

1. Wartość indeksów l, r i sr będą sobie równe – Jeśli element pod indeksem sr, będzie większy od elementu wstawianego, szukana pozycja to sr-1, w przypadku kiedy będzie mniejszy, szukaną pozycją będzie sr+1 (można także skorzystać z notacji l+1).
2. Wartość indeksu l, jest większa od r – należy sprawdzić czy wartość elementu znajdującego się pod indeksem l, jest większa od wstawianego elementu. Jeśli tak, wstawiamy nasz elementu na l+1, jeśli nie, na pozycję wskazywaną przez indeks l.

Jeśli sortujemy tablicę, w której wartości poszczególnych elementów powtarzają się, podczas porównywania elementów dodajemy jeden prosty warunek. Jeżeli wartość elementu pod indeksem sr, będzie równa wartości wstawianego elementu, to nowa pozycja tego elementu wynosić będzie sr+1, kończąc przy tym wyszukiwanie.

Trochę praktyki

Algorytmy najlepiej poznawać na przykładach, tak wykonajmy kilka pierwszych kroków sortowania binarnego.

Weźmy zbiór [15, 63, 1, 81, 9]. Zaczynamy od wstawienia elementu o wartości 63, na miejsce docelowe. Wyznaczamy środek posortowanego już zbioru – w tym przypadku zbioru zawierającego jedynie element 15, a co za tym idzie jego środek znajduje się pod indeksem 0. Indeksy l,r i sr, są sobie równe, więc mamy element zbioru uporządkowanego, mający wartość najbliższą elementowi wstawianemu. Jako, że 63 jest większe od 15, jego docelowe miejsce znajduje się pod indeksem równym 1, czyli element ten nie zmienia pozycji.

Przechodzimy do kolejnego kroku. Tym razem wykonujemy porównanie dla elementu o wartości 1. Wyznaczamy wartość indeksu sr, dla l = 0 i r=1. Wartość indeksu środkowego ponownie wynosi 0. Wykonujemy porównanie. 1 jest mniejsze od 15. Jako, że indeksy l i r nie są równe, musimy wyznaczyć nową podtablicę, gdzie r = sr – 1. W kolejnym kroku wyszukiwania zauważamy, że wartość indeksu l jest większa od r (l = 0, r = -1), oznacza to, że trafiliśmy na jeden z warunków zakończenia algorytmu wyszukiwania. By otrzymać miejsce na które mamy wstawić nasz element, musimy jedynie sprawdzić, czy element wstawiany jest większy, od elementu pod indeksem l. Nie jest tak (15 > 1), więc element o wartości 1, wstawiony zostaje na pozycję 0, a pozostałe elementy przesunięte w głąb tablicy.

Na wykonanie pojedynczych kroków algorytmu, potrzebowaliśmy wykonać dość dużo porównań. Aby więc ułatwić zrozumienie algorytmu, spójrzmy na animację obrazującą sortowanie binarne całego powyższego zbioru:

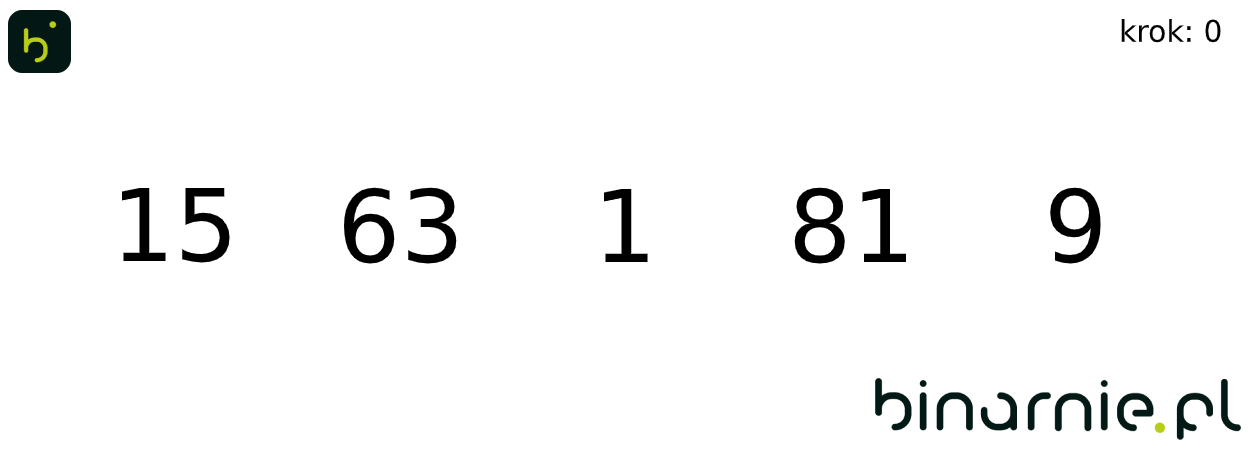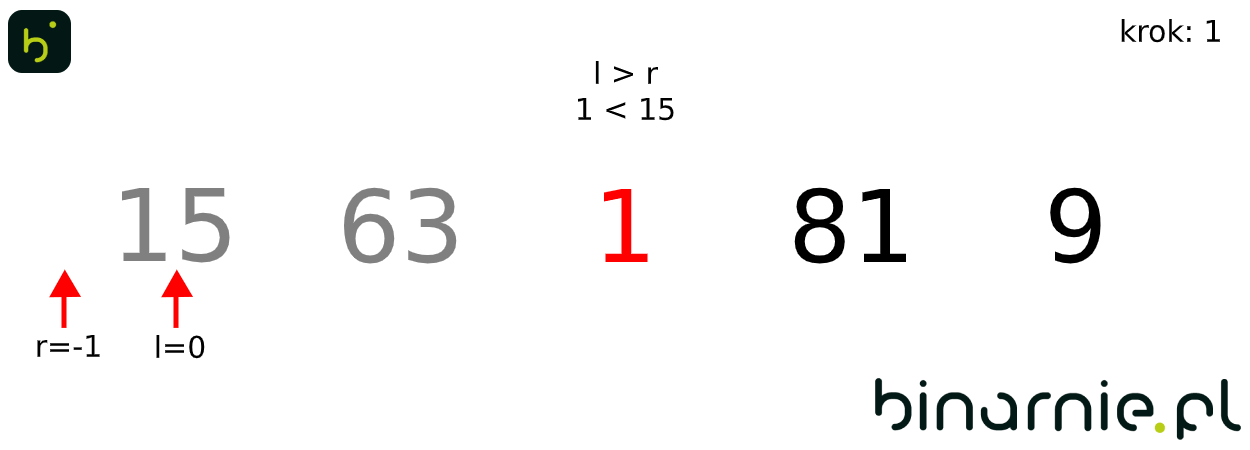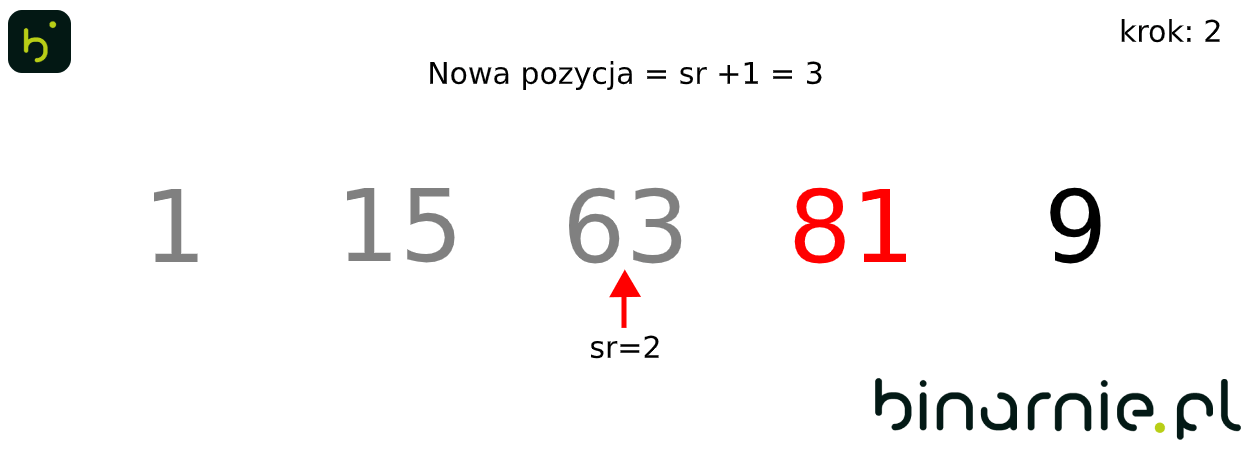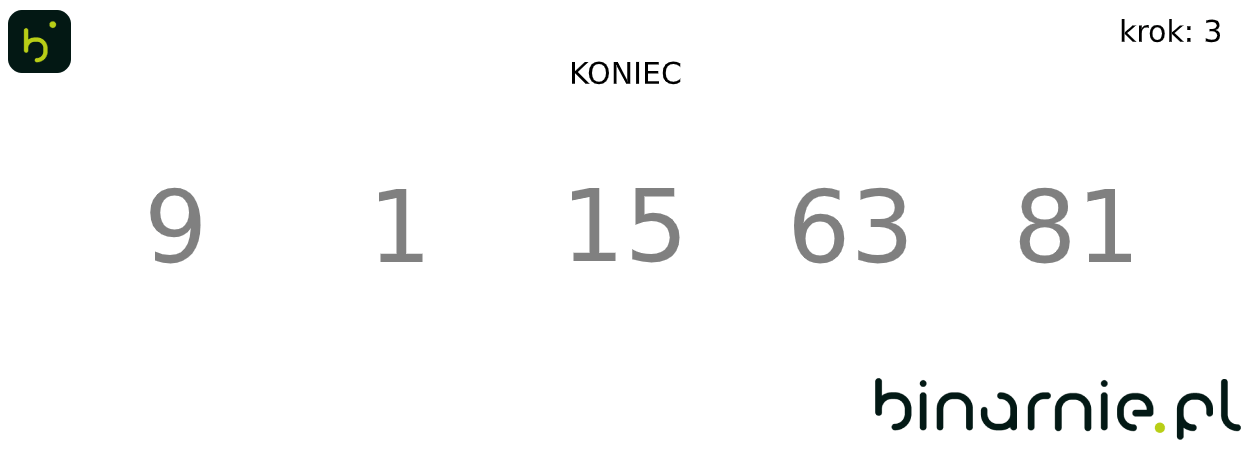
Właściwości

Optymistyczna złożoność sortowania binarnego wynosi O(nlogn), więc teoretycznie, powinien być on szybszy od zwykłego sortowania przez wstawianie. Zauważcie jednak ile porównań musieliśmy wykonać, już w drugim kroku tego algorytmu, gdzie przy przeszukiwaniu liniowym, byłoby ich znacznie mniej.

Puenta jest więc następująca – owszem sortowanie binarne jest szybsze od sortowania przez wstawianie, ale jedynie dla większych zbiorów. W przypadku małych zbiorów, jak ten z przykładu powyżej, jest on wolniejszy, lub ledwo porównywalnie szybszy.

Sortowanie binarne – implementacje

C++

Java

Python

Podsumowanie

Rozgryzanie sortownia binarnego właśnie za nami. Mimo tego, że był to,
w porównaniu do poprzednich, nieco cięższy kawałek algorytmu, dobrnęliście ze mną do końca. Jeśli jesteście ciekawi działania kolejnych algorytmów, serdecznie zapraszam was za tydzień, na kolejną część „Piątku z sortowaniem” 😊.