Klasycznie już, wraz z kolejnym piątym dniem tygodnia, przed wami kolejna część „Piątku z sortowaniem”. Tym razem rozgryziemy wspólnie sposób działania algorytmu sortowania przez zliczanie (counting sort) oraz przyjrzymy się przykładowej implementacji.
Sortowanie przez zliczanie –algorytm
Sortowanie przez zliczanie, jest łudząco podobne do sortowania kubełkowego, omawianego tydzień temu. Ponownie zliczać będziemy wystąpienia poszczególnych elementów, by na końcu stworzyć tablicę, którą wypełnimy odpowiednimi wartościami. Ich ilość podyktowana będzie przez liczniki.
Algorytm ten podzielony jest na kilka kroków:
- Wyznaczamy wartość ymin i ymax.
- Tworzymy tablicę liczników, której rozmiar obliczamy ze wzoru ymax – ymin + 1.
- Przechodzimy przez zbiór wejściowy, zliczając wystąpienia poszczególnych elementów przy pomocy tablicy liczników.
- Do tablicy docelowej dodajemy elementy, których wartość podyktowana jest przez wzór: indeks tablicy liczników + ymin, a ilość tych elementów przez wartość licznika na rozpatrywanej pozycji.
W ten właśnie sposób otrzymujemy posortowaną tablicę.

Sortowanie przez zliczanie – przykład
By w pełni zrozumieć ten algorytm, spójrzmy na przykład. Weźmy zbiór {4, 2, 5, 6, 1, 4, 6, 6, 4}. W pierwszym kroku wyznaczmy wartość maksymalną i minimalną w danym zbiorze. W tym przypadku wynoszą one:
ymin = 1; ymax =6
Korzystając ze wzoru ymax – ymin + 1 wiemy, że tablica liczników, musi mieć rozmiar 6. Na potrzeby pisemnego przykładu stwórzmy ją według wzorca [ wartość zliczanego elementu: liczba wystąpień; …]:
[1:0; 2:0; 3:0; 4:0; 5:0; 6:0]
Idąc zgodnie z krokami algorytmu, zliczamy teraz liczbę wystąpień poszczególnych elementów, poruszając się od początku do końca zbioru. Daje nam to wyjściową tablicę liczników:
[1:1; 2:1; 3:0; 4:3; 5:1; 6:3]
Po zliczeniu wystąpień elementów, możemy zabrać się za tworzenie nowego zbioru, dodając do niego elementy o wartości i ilości podyktowanej przez licznik. Nasz zbiór, będzie wyglądał następująco:
{1, 2, 4, 4, 4, 5, 6, 6, 6}
Zbiór ten jest posortowanym zbiorem wejściowym, co kończy nasz algorytm. By jeszcze lepiej zrozumieć działanie tego algorytmu spójrzmy na wizualizację powyższego przykładu:
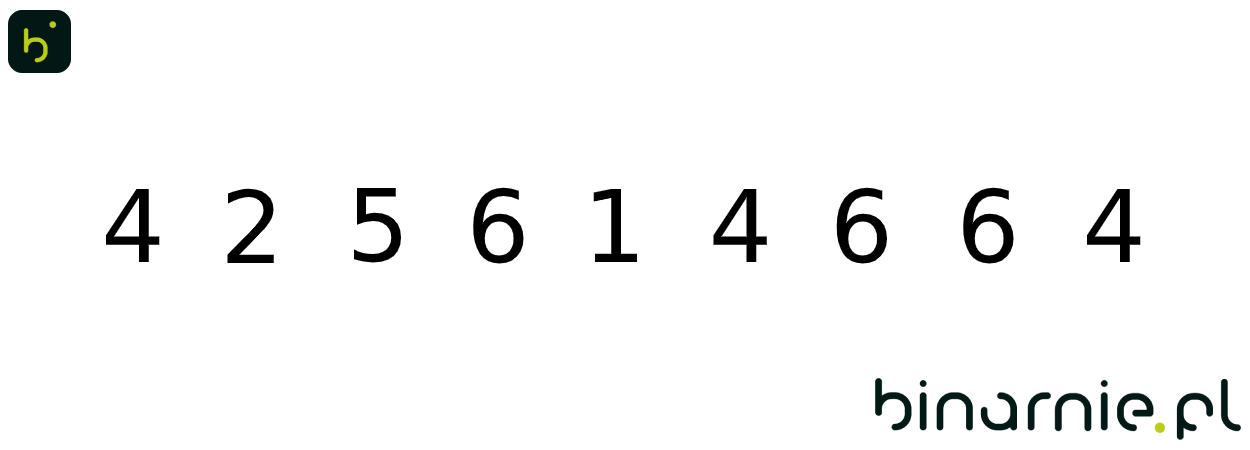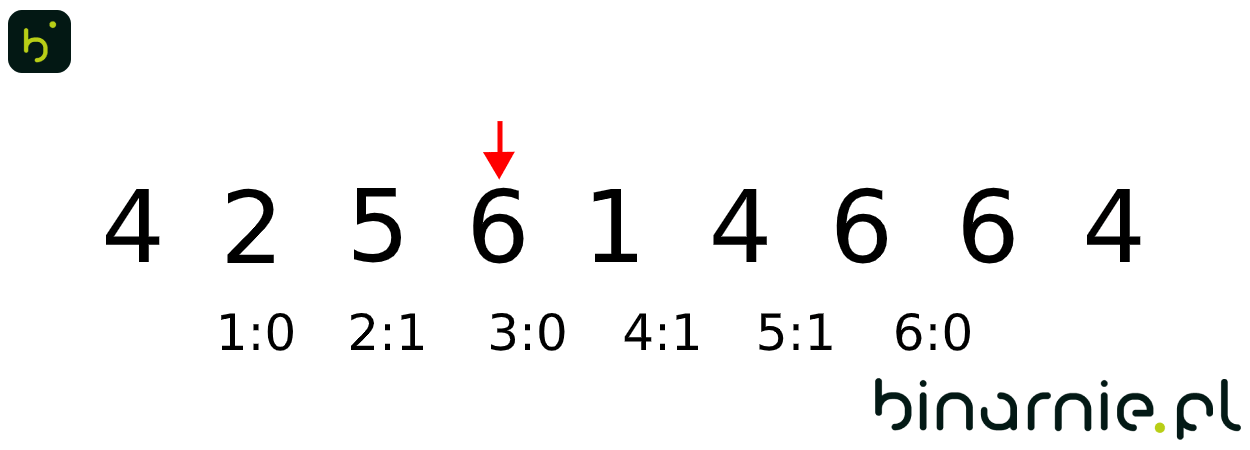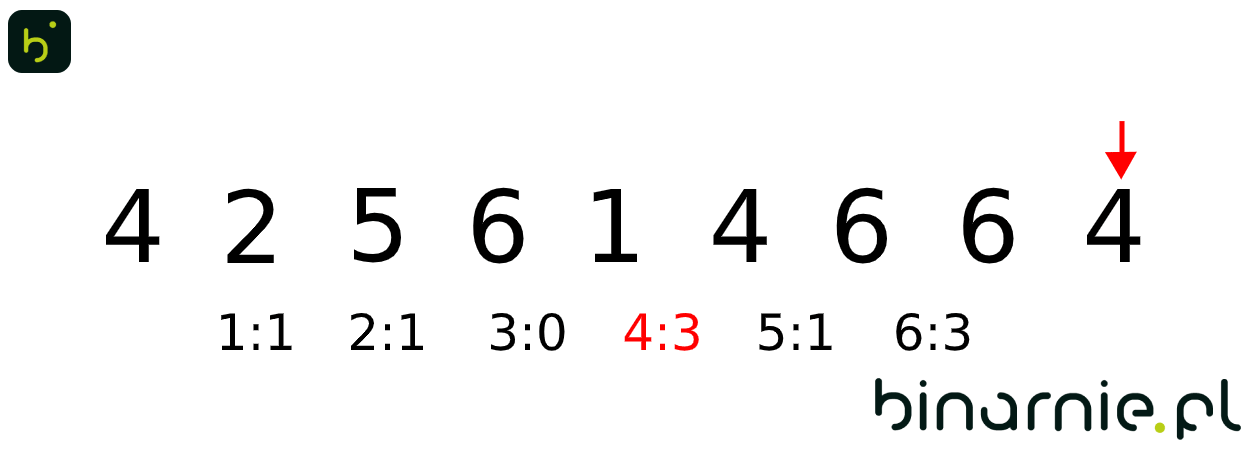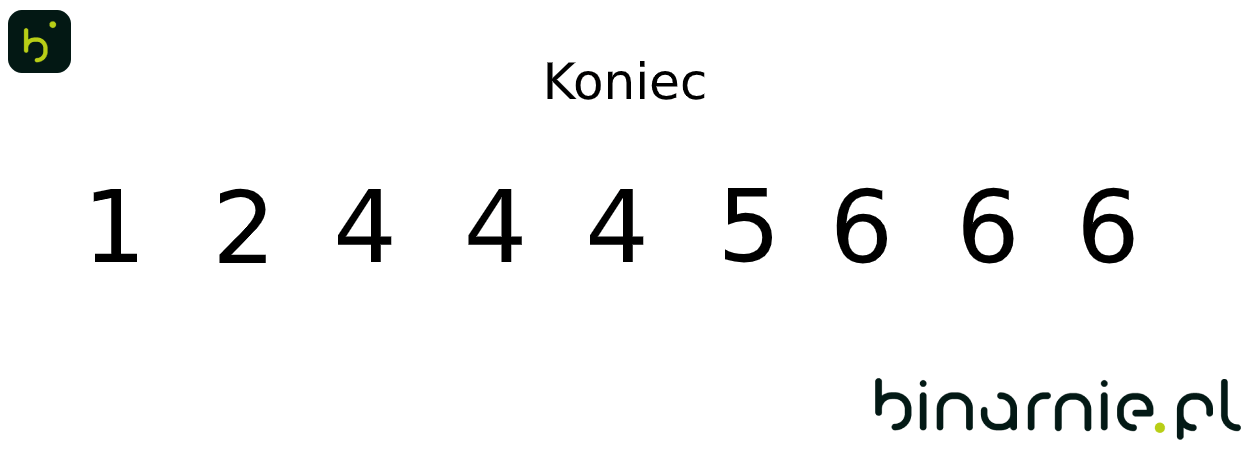
Sortowanie przez zliczanie – implementacje
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 |
//program do sortowania n-elementowej tablicy //przy pomocy algorytmu sortowania kubełkowego //dla liczb całkowitych dodatnich //Jan Żwirek #include <iostream> using namespace std; void printTab(int *tab, int n); int* findMinAndMax(int* tab, int n); void counting_sort(int *tab, int n, int yMin, int yMax) { int* counters = new int[yMax - yMin + 1]; //Wstawiamy początkowe wartości liczników for (int x = 0; x < (yMax - yMin + 1); x++) { counters[x] = 0; } cout << endl << "Stworzono tablice licznikow: " << endl; cout << "\t| "; for (int x = 0; x < (yMax - yMin + 1); x++) { cout << x + yMin << ":0 | "; } cout << endl; for (int x = 0; x < n; x++) { //Zliczamy ilość wystąpień poszczególnych elementów counters[tab[x] - yMin]++; } cout << endl << "Zliczono elementy: " << endl; cout << "\t| "; for (int x = 0; x < (yMax - yMin + 1); x++) { cout << x + yMin << ":" << counters[x] << " | "; } cout << endl; //Zapisujemy elementy w ilości podyktowanej przez liczniki //w tablicy docelowej int lastIndex = 0; for (int x = 0; x < (yMax - yMin + 1); x++) { int y; for (y = lastIndex; y < counters[x] + lastIndex; y++) { tab[y] = x + yMin; } lastIndex = y; } } int main() { int n; cout << "Wprowadz liczbe elementow tablicy: "; cin >> n; //Dynamiczne tworzenie tablicy int *tab = new int[n]; cout << "\nWprowadz " << n << " liczb do posortowania" << endl; cout << "Zatwierdz kazda z nich klawiszem Enter:" << endl; for (int x = 0; x < n; x++) { cin >> tab[x]; } cout << endl << "Tablica przed posortowaniem:" << endl; printTab(tab, n); int* minAndMax = findMinAndMax(tab, n); cout << endl << "Minimalny element tablicy: " << minAndMax[0] << endl; cout << "Maksymalny element tablicy: " << minAndMax[1] << endl; cout << endl << "Rozpoczecie sortowania" << endl; counting_sort(tab, n, minAndMax[0], minAndMax[1]); cout << endl << "Oto tablica po sortowaniu:" << endl; printTab(tab, n); delete[] tab; delete[] minAndMax; system("pause"); return 0; } void printTab(int *tab, int n) { cout << endl << "\t| "; for (int x = 0; x < n; x++) { cout << tab[x] << " | "; } cout << endl << endl; } //Funkcja do wyszukiwania największej i //najmniejszej wartości w tablicy int* findMinAndMax(int* tab, int n) { int* minAndMax = new int[2]; minAndMax[0] = tab[0]; minAndMax[1] = tab[0]; for (int x = 0; x < n; x++) { if (tab[x] < minAndMax[0]) { minAndMax[0] = tab[x]; } if (tab[x] > minAndMax[1]) { minAndMax[1] = tab[x]; } } return minAndMax; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 |
package matura; import java.util.Scanner; public class Main { private static void printArray(int[] tab) { System.out.println(); for(int i = 0; i < tab.length; i++) { System.out.print(tab[i] + " | "); } System.out.println(); } private static int[] getMinMax(int[] arr) { int[] result = new int[2]; result[0] = arr[0]; // pierwszy element bedzie najmniejszym elementem result[1] = arr[0]; // drugi element bedzie najwiekszym elementem for(int i : arr) { if(result[0] > i) { //dokonujemy podmiany najwiekszego/najmniejszego elementu w przypadku gdy iterowana wartosc bedzie wieksza/mniejsza od przechowanej result[0] = i; } else if (result[1] < i) { result[1] = i; } } return result; } private static void countingSort(int[] tab) { int[] minmax = getMinMax(tab); int yMin = minmax[0]; int yMax = minmax[1]; int[] counters = new int[yMax - yMin + 1]; //Wstawiamy początkowe wartości liczników for (int x = 0; x < (yMax - yMin + 1); x++) { counters[x] = 0; } System.out.println("Stworzono tablice licznikow: "); for (int x = 0; x < (yMax - yMin + 1); x++) { System.out.print((x + yMin) + ":" + counters[x] + "| "); } System.out.println(); for (int x = 0; x < tab.length; x++) { //Zliczamy ilość wystąpień poszczególnych elementów counters[tab[x] - yMin]++; } System.out.println("Zliczono elementy: "); for (int x = 0; x < (yMax - yMin + 1); x++) { System.out.print((x + yMin) + ":" + counters[x] + "| "); } System.out.println(); //Zapisujemy elementy w ilości podyktowanej przez liczniki //w tablicy docelowej int lastIndex = 0; for (int x = 0; x < (yMax - yMin + 1); x++) { int y; for (y = lastIndex; y < counters[x] + lastIndex; y++) { tab[y] = x + yMin; } lastIndex = y; } } public static void main(String[] args){ Scanner sc = new Scanner(System.in); //inicjalizujemy Scanner - obiekt pozwalajacy na wczytywanie zmiennych od uzytkownika System.out.println("Wprowadz liczbe elementow tablicy: "); int n = sc.nextInt(); int[] arr = new int[n]; for(int i = 0; i < n; i++) { System.out.println("Podaj element nr." + i + ": "); arr[i]= sc.nextInt(); //wczytujemy kolejne elementy tablicy } System.out.println("Oto wprowadzona tablica:"); printArray(arr); System.out.println(); countingSort(arr); System.out.println(); System.out.println("Oto wprowadzona tablica po przesortowaniu:"); printArray(arr); sc.close(); //zwalniamy zasoby } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
def wypisz(tab): # tworzymy metode do wypiswania zawartosci naszej tablicy for el in tab: print(el, end=" | ") def minMax(tab): #tworzymy funkcje znajdujaca najwiekszy i najmniejszy element min = tab[0] #tworzymy zmienne pomocnicze max = tab[0] for el in tab: if el > max: # a nastepnie sprawdzamy czy sa one wieksz, lub mniejsze od iterowanej wartosci max = el if el < min: min = el array = [] array.append(min) #na koniec wrzucamy je w tablice array.append(max) return array def sortujZlicz(tab, n): minmax = minMax(tab) #pobieramy skrajne elementy tablicy min = minmax[0] max = minmax[1] countersSize = max - min + 1 #liczymy potrzebna ilosc elementow counters = [0] * countersSize #i od razu tworzymy tablice licznikow print("Stworzono tablice licznikow: ") for x in range(countersSize): print(x+min, "=0", end=" | ") print() for x in range(n): counters[tab[x] - min] += 1 #zliczamy ilosc elementow print("Zliczono ilosc elementow: ") for x in range(countersSize): print(x+min, "=", counters[x], end=" | ") print() lastIndex = 0 for x in range(countersSize): # a nastepnie wstawiamy je kolejno w wyjsciowa tablice y = lastIndex while y < counters[x] + lastIndex: tab[y] = x + min y += 1 lastIndex = y print("Podaj ilosc elementow tablicy:") a = int(input()) tablica = [] for i in range(a): print("Podaj element nr. ", (i + 1)) tablica.append(int(input())) print("Oto twoja tablica:") wypisz(tablica) sortujZlicz(tablica, a) print("Oto twoja tablica po sortowaniu:") wypisz(tablica) |
Trochę teorii
Sortowanie przez zliczanie jest niezwykle szybkie – ma złożoność obliczeniową O(n+m), gdzie m to rozpiętość danych. Podobnie jak w przypadku algorytmu sortowania kubełkowego, gdy sortujemy zbiór o dużej liczności i stosunkowo małym zakresie wartości elementów, algorytm zbliża się do złożoności O(n) – czyli złożoności liniowej.
Oczywiście, nic nie może być idealne i tak jest również w przypadku tegoż algorytmu. Po pierwsze, w przypadku zbiorów o większej rozpiętości danych, radzi on sobie znacznie gorzej, niż chociażby sortowanie przez kopcowanie. Kolejną wadą, jest potrzeba znajomości zakresu wartości zbioru, przed rozpoczęciem sortowania. Jeśli nie znamy zakresu, efektywność algorytmu ponownie spada, z powodu potrzeby przejścia przez cały zbiór i znalezienia największego oraz najmniejszego elementu. Złożoność czasowa zmienia się więc na O(2n+m). Dodatkowo, jest on praktycznie niemożliwy do wykorzystania, w przypadku liczb ułamkowych, chyba że ograniczymy się do liczb konkretnego rzędu. Mimo tego, że ograniczenie rzędu umożliwia zaimplementowanie algorytmu, w takim scenariuszu, jego efektywność tragicznie spada. Czemu tak jest?
Przypadek nadzwyczajny
Za przykład weźmy malutki zbiór ułamków dziesiętnych, ograniczonych do dwóch miejsc po przecinku np.: { 2.31, 1.89, 2.11 }. W przypadku takiego zbioru, mimo tego, że wartości elementów nie różnią się od siebie znacząco, musimy stworzyć tablicę liczników o rozmiarze, aż 43! Nasza rozpiętość wartości jest więc dość duża. Jeśli spojrzycie, na funkcję sortowania w implementacji powyżej, możecie zauważyć, że w trzeciej z pętli, będziemy musieli przejść przez całą tablicę liczników, by uzupełnić tablicę docelową. Wyobraźcie sobie, co by się stało, dla zakresu od 0.99 do 100.99.
W praktyce, algorytm ten jest więc wykorzystywany, jedynie dla liczb całkowitych i to tylko w specyficznych przypadkach, przez potrzebę znajomości zakresu.
Podsumowanie
Płynąc meandrami wiedzy algorytmicznej, minęliśmy kolejny kamień milowy w postaci sortowania przez zliczanie. Jeśli chcecie jak najlepiej przygotować się na nadchodzącą maturę z informatyki i wciąż jesteście głodni wiedzy, zapraszam was za tydzień na kolejny wpis z serii „Piątek z sortowaniem”. Zajrzyjcie również, do zakładki matura z informatyki, gdzie znajdziecie inne materiały do nauki.





