Oto wpis którego nie może zabraknąć w piątek. W kolejnej części „Piątku z sortowaniem”, dowiemy się jak działa oraz jak zaimplementować algorytm sortowania szybkiego. Tak więc, bez zbędnego przedłużania, zaczynajmy.
Sortowanie szybkie – algorytm
Sortowanie szybkie (quick sort), to algorytm rekurencyjny opierający na metodzie dziel i zwyciężaj. Dzielimy w nim tablicę wejściową, na mniejsze podtablice. Wykonujemy to, wyznaczając podział z wykorzystaniem punktu osiowego (pivot), zwanego inaczej elementem rozdzielającym.
Istnieje kilka wersji algorytmu sortowania szybkiego, które różnią się od siebie sposobem wyboru punktu osiowego. My wybierzemy wersję, w której punkt osiowy jest zawsze pierwszym elementem tablicy. Jak wyglądają kroku tego algorytmu?
- Jeżeli rozmiar rozpatrywanej tablicy jest równy jeden, kończymy algorytm.
- Wyznaczamy punkt osiowy, który w naszym przypadku jest pierwszym elementem tablicy.
- Dokonujemy wstępnego przesortowania. Przechodzimy kolejno przez elementy tablicy, przyrównując je do wartości punktu osiowego. Jeśli rozpatrywany element jest większy, pozostawiamy go na miejscu, jeżeli jest mniejszy, bądź równy zamieniamy go miejscami z pierwszym elementem większym od punktu osiowego. Jeśli nie ma elementów większych, pozostawiamy element mniejszy na miejscu.
- Gdy przejdziemy przez całą tablicę, zamieniamy miejscami punkt osiowy, z ostatnim elementem mniejszym od niego. W ten sposób punkt osiowy znajduje się pomiędzy elementami mniejszymi, a większymi o niego. Elementy w podtablicach nie są jeszcze posortowane.
- Ponownie rozpatrujemy algorytm (zaczynając od kroku pierwszego) dla lewej i prawej części tablicy.
Przykład
Nic bardziej nie ułatwi zrozumienie działania algorytmu jak prosty przykład. Weźmy zbiór:
{5, 3, 6, 1, 7, 2}
Naszym punktem osiowym jest element 5. Zaczynamy więc wstępne przesortowanie. W pierwszym kroku porównywania napotykamy element mniejszy od punktu osiowego, jako że brak jest elementów większych pozostawiamy go na miejscu. 6 jest większe, więc również pozostaje na miejscu. Pierwsza zmiana elementów miejscami następuje w przypadku 1, które zostaje zamienione miejscami z 6 dając nam:
{5, 3, 1, 6, 7, 2}
Kolorami zaznaczone zostały rozpatrzone elementy – kolor żółty odpowiada elementom mniejszym od punktu osiowego, a czerwony większym. W kolejnych krokach pozostawiamy element 7 na miejscu, a element 2, zamieniamy miejscami z elementem 6, otrzymując:
{5, 3, 1, 2, 7, 6}
Ostatnim krokiem przed rozpatrzeniem algorytmu dla podtablic, jest zamiana miejscami punktu osiowego, z ostatnim elementem mniejszym od niego. Daje nam to zbiór w postaci:
{2, 3, 1, 5, 7, 6}
Widzimy, że wstępne posortowanie zostało wykonane poprawnie, ponieważ elementy mniejsze znajdują się na lewo od punktu osiowego, a elementy większe, na prawo. Ponownie rozpatrujemy więc algorytm, dla podtablic {2,3,1} oraz {7,6}. Resztę kroków tego przykładu, możecie zobaczyć na animacji poniżej:G
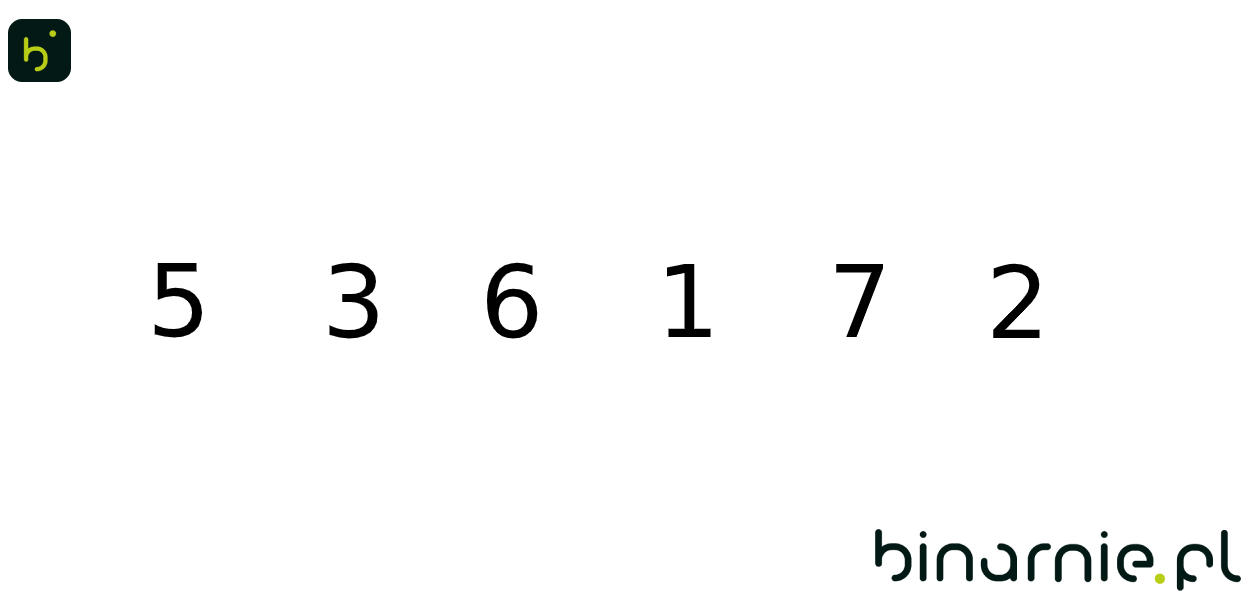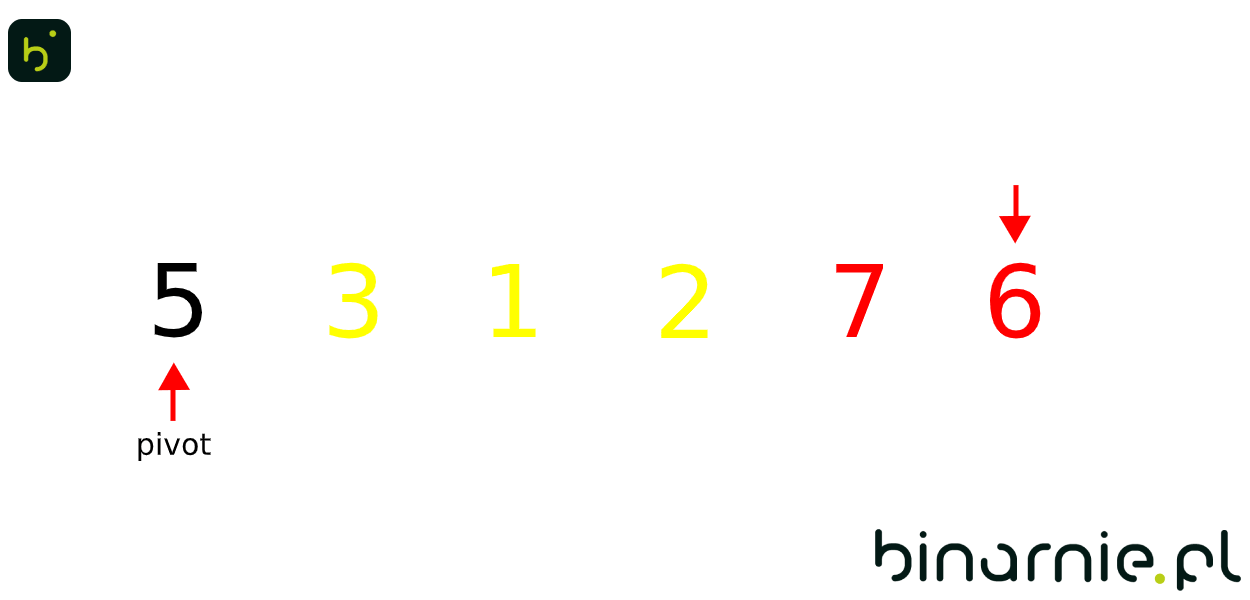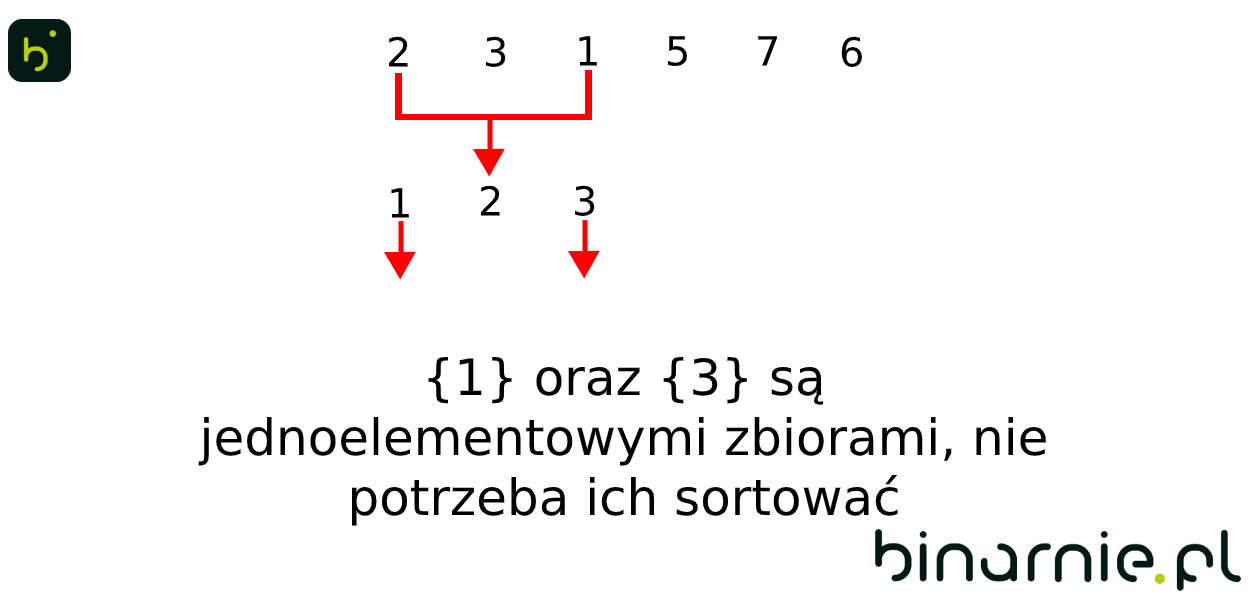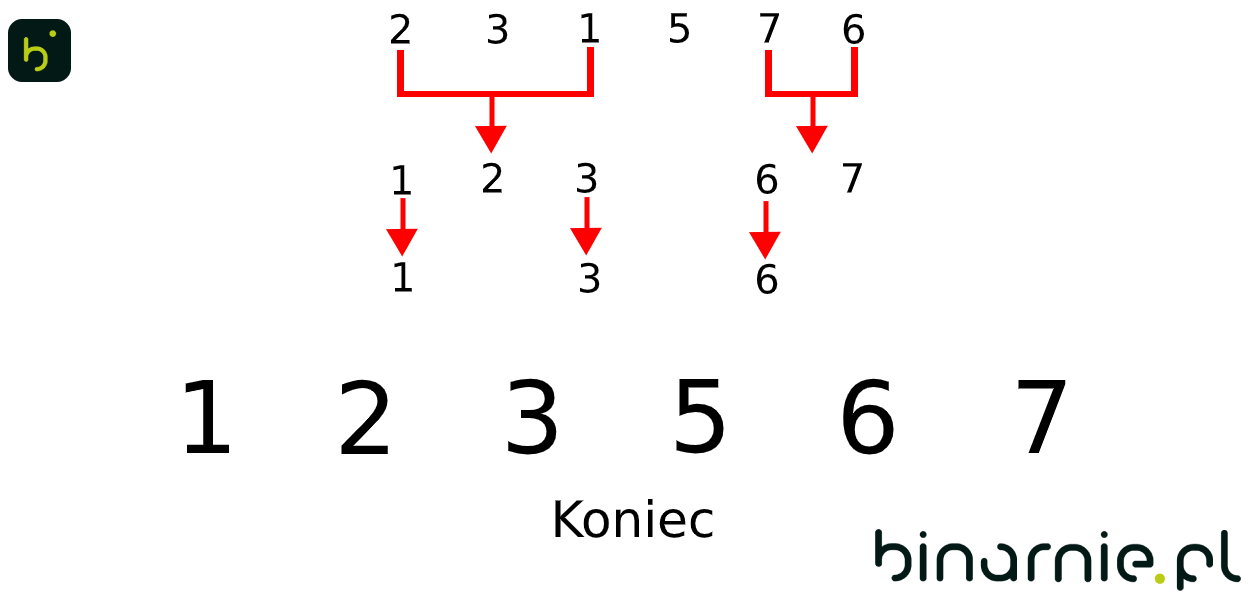
Sortowanie szybkie – implementacje
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 |
//program do sortowania n-elementowej tablicy //przy pomocy algorytmu sortowania szybkiego //Jan Żwirek #include <iostream> #include <algorithm> using namespace std; void printTab(int *tab, int indexLow, int indexHigh); void quick_sort(int *tab, int indexLow, int indexHigh) { //Jeśli tablica ma tylko jeden element kończymy algorytm if (indexLow >= indexHigh || indexLow < 0 || indexHigh < 0) { return; } //Tworzymy zmienną piwot by przechowywać wartość punktu osiowego int pivot = tab[indexLow]; //lowerNumbersEndIndex wskazuje pozycję na którą wstawiamy elementy mniejsze od punktu osiowego int lowerNumbersEndIndex = indexLow + 1; for (int iterator = indexLow+1; iterator <= indexHigh; iterator++) { //Po napotkaniu mniejszego bądź równego elementu, zamieniamy go miejscami //z piwerwszym większym elementem if (tab[iterator] <= pivot) { swap(tab[lowerNumbersEndIndex], tab[iterator]); lowerNumbersEndIndex++; } } //Wstawiamy punkt osiowy we właściwe miejsce w tablicy swap(tab[indexLow], tab[lowerNumbersEndIndex - 1]); cout << "Podtablica " <<indexLow << ":" << indexHigh << endl; printTab(tab, indexLow, indexHigh); //Wywołujemy algorytm rekurencyjnie, dla lewej i prawej podtablicy quick_sort(tab, indexLow, lowerNumbersEndIndex-2); quick_sort(tab, lowerNumbersEndIndex, indexHigh); } int main() { unsigned int n; cout << "Wprowadz liczbe elementow tablicy: "; cin >> n; //Dynamiczne tworzenie tablicy int *tab = new int[n]; cout << "\nWprowadz " << n << " liczb do posortowania" << endl; cout << "Zatwierdz kazda z nich klawiszem Enter:" << endl; for (int x = 0; x < n; x++) { cin >> tab[x]; } cout << endl << "Tablica przed posortowaniem:" << endl; printTab(tab, 0, n-1); cout << endl << "Rozpoczecie sortowania" << endl; quick_sort(tab, 0, n-1); cout << endl << "Oto tablica po sortowaniu:" << endl; printTab(tab, 0, n-1); delete[] tab; system("pause"); return 0; } void printTab(int *tab, int indexLow, int indexHigh) { cout << endl << "\t| "; for (int x = indexLow; x <= indexHigh; x++) { cout << tab[x] << " | "; } cout << endl << endl; } |
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
package matura; import java.util.Scanner; public class Main { private static void printArray(int[] tab, int low, int high) { System.out.print("| "); for(int i = low; i <= high; i++) { System.out.print(tab[i] + " | "); } System.out.println(); System.out.println(); } private static void quick_sort(int[] tab, int indexLow, int indexHigh) { //Jeśli tablica ma tylko jeden element kończymy algorytm if (indexLow >= indexHigh || indexLow < 0 || indexHigh < 0) { return; } //Tworzymy zmienną piwot by przechowywać wartość punktu osiowego int pivot = tab[indexLow]; //lowerNumbersEndIndex wskazuje pozycję na którą wstawiamy elementy mniejsze od punktu osiowego int lowerNumbersEndIndex = indexLow + 1; for (int iterator = indexLow+1; iterator <= indexHigh; iterator++) { //Po napotkaniu mniejszego bądź równego elementu, zamieniamy go miejscami //z pierwszym większym elementem if (tab[iterator] <= pivot) { int pom = tab[lowerNumbersEndIndex]; tab[lowerNumbersEndIndex] = tab[iterator]; tab[iterator] = pom; lowerNumbersEndIndex++; } } //Wstawiamy punkt osiowy we właściwe miejsce w tablicy int pom = tab[lowerNumbersEndIndex - 1]; tab[lowerNumbersEndIndex - 1] = tab[indexLow]; tab[indexLow] = pom; System.out.println("Podtablica " +indexLow + ":" + indexHigh); printArray(tab, indexLow, indexHigh); //Wywołujemy algorytm rekurencyjnie, dla lewej i prawej podtablicy quick_sort(tab, indexLow, lowerNumbersEndIndex-2); quick_sort(tab, lowerNumbersEndIndex, indexHigh); } public static void main(String[] args){ Scanner sc = new Scanner(System.in); //inicjalizujemy Scanner - obiekt pozwalajacy na wczytywanie zmiennych od uzytkownika System.out.println("Wprowadz liczbe elementow tablicy: "); int n = sc.nextInt(); int[] arr = new int[n]; for(int i = 0; i < n; i++) { System.out.println("Podaj element nr." + i + ": "); arr[i]= sc.nextInt(); //wczytujemy kolejne elementy tablicy } System.out.println("Oto wprowadzona tablica:"); printArray(arr, 0, n-1); System.out.println(); quick_sort(arr, 0, n-1); System.out.println(); System.out.println("Oto wprowadzona tablica po przesortowaniu:"); printArray(arr, 0, n-1); sc.close(); //zwalniamy zasoby } } |
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
def wypisz(tab, low, high): # tworzymy metode do wypiswania zawartosci naszej tablicy print() for e in range(low, high+1): print(tab[e], end=" | ") print() print() def sortujQuick(tab, iLow, iHigh): #tworzymy rekurencyjna funkcje sortujaca if iLow >= iHigh or iLow < 0 or iHigh < 0: #warunek stop return pivot = tab[iLow] #tworzymy zmienna osiowa lowerNumsEndIndex = iLow + 1 #oraz zmienna wskazujaca na pozycje, na ktora bedziemy wstawiac elementy mniejsze od pivot for i in range(iLow + 1, iHigh+1): if tab[i] <= pivot: #po napotkaniu elementu mniejszego, badz rownego zamiemay miejscami z pierwszym wiekszym pom = tab[i] tab[i] = tab[lowerNumsEndIndex] tab[lowerNumsEndIndex] = pom lowerNumsEndIndex += 1 pom = tab[iLow] #Wstawiamy punkt osiowy we właściwe miejsce w tablicy tab[iLow] = tab[lowerNumsEndIndex-1] tab[lowerNumsEndIndex - 1] = pom print("Podtablica ", iLow, ":", iHigh) wypisz(tab, iLow, iHigh) sortujQuick(tab, iLow, lowerNumsEndIndex-2) #Wywołujemy algorytm rekurencyjnie, dla lewej i prawej podtablicy sortujQuick(tab, lowerNumsEndIndex, iHigh) print("Podaj ilosc elementow tablicy:") a = int(input()) tablica = [] for i in range(a): print("Podaj element nr. ", (i + 1)) tablica.append(int(input())) print("Oto twoja tablica:") wypisz(tablica, 0, a-1) sortujQuick(tablica, 0, a-1) print("Oto twoja tablica po sortowaniu:") wypisz(tablica, 0, a-1) |
Teoria
To co można zauważyć w pierwszej kolejności, chociażby przez nazwę algorytmu, to jego wydajność. Złożoność obliczeniowa plasuje się na poziomie O(nlogn). Szybkość tego algorytmu, zależy głównie od doboru punktu osiowego – im bliżej mediany jest pivot, tym lepej. Jeśli podział jest w miarę zrównoważony, szybkość algorytmu jest naprawdę wysoka. W przypadku przeciętnym złożoność rośnie do O(2nlnn), co wciąż jest dobrym wynikiem. W przypadku pesymistycznym osiąga on złożoność obliczeniową O(n2), czyli taką samą jak chociażby sortowanie przez wybieranie.
Możemy usprawnić działanie algorytmu, w celu przybliżenia go do złożoności O(nlogn). Dokonamy tego chociażby poprzez losowanie elementu osiowego, dzięki czemu zmniejszymy prawdopodobieństwo trafienia na element największy lub najmniejszy.
Co ciekawe mimo swojej nazwy, algorytm sortowania nie jest najszybszym z wszystkich dostępnych algorytmów. Owszem w przypadku optymistycznym, jest bardzo wydajny, jednakże prawdopodobieństwo natrafienia na przypadek pesymistyczny lub pośredni, jest dość duże. Szybszym od niego jest chociażby sortowanie przez kopcowanie, które ma zawsze gwarantowaną złożoność O(nlogn). Algorytm ten, omówimy w przyszłości.
Podsumowanie
Sortowanie szybkie jest ważnym osiągnięciem, w rozwijaniu naszej wiedzy algorytmicznej. Jest to pierwszy z algorytmów o złożoności O(nlogn), który wspólnie poznaliśmy. Właśnie takie algorytmy, są zazwyczaj wykorzystywane w praktyce.

Jeśli wciąż jesteście głodni wiedzy, lub chcecie jeszcze lepiej przygotować się na maturę z informatyki, zapraszam was do naszej grupy wsparcia na Facebooku. Znajdziecie tam różnorodne materiały, do przygotowania się na maturę z informatyki.





