Matura z informatyki 2021 rozwiązania C++, Java, Python

Mija już miesiąc odkąd matura z informatyki 2021 dobiegła końca. Opinie maturzystów co do jej trudności są jak zawsze podzielone: jedni uważają, że była znacznie łatwiejsza niż zeszłoroczne, podczas gdy inni wyszli po kilku minutach z praktyki łapiąc się za głowę. W tym roku jednak większość opinii skłaniała się ku stwierdzeniu, że ten egzamin był łatwy. Niezależnie jednak od trudności tegorocznej matury publikujemy dla Was jej rozwiązania, wraz ze szczegółowym omówieniem. Jeżeli szukacie odpowiedzi do matur z poprzednich lat, to znajdziecie je również na naszym blogu:

Zanim przejdziemy do omówienia zadań przypomnijmy w jakim schemacie przebiega matura z informatyki. Egzamin ten jest podzielony na dwie części:

Teorię, która trwa 60 minut, a do jej rozwiązania możemy wykorzystać jedynie kartkę, długopis oraz kalkulator. Część ta zazwyczaj składa się z analizy algorytmu, pewnego problemu i stworzenie algorytmu do jego rozwiązania, a także zadania z odpowiedziami typu zamkniętego
Praktykę, która trwa 150 minut, a do jej rozwiązania wykorzystujemy komputer, a w nim wszelkie dostępne narzędzia, o których mowa w poleceniu. Zazwyczaj jedno zadanie wymaga od zadającego napisania własnego programu w wybranym wcześniej środowisku i języku programowania, podczas gdy dwa pozostałe zadania pozostawiają dowolność w wyborze narzędzi

Uwaga: CKE nie opublikowała jeszcze klucza odpowiedzi do matur, więc, z racji iż nie mamy jak ich zweryfikować, to niektóre odpowiedzi mogą zawierać błędy.

Matura z informatyki 2021 – część pierwsza

Tak jak co roku część teoretyczna składała się z trzech różnych zadań, za których poprawne wykonanie można było uzyskać 15 punktów, co daje 30% z całej matury. W mojej opinii część ta była znacznie łatwiejsza, niż w poprzednich latach – darmowe punkty do rekrutacji na studiach. Nie przedłużając przejdźmy do rozwiązywania zadań:

Matura z informatyki 2021 zadanie 1 – cyfrowe dopełnienie

Zadanie dosyć proste. Każdą liczbę możemy zapisać jako sumę iloczynów jednej cyfr <0, 9> z kolejnymi potęgami dziesiątki (wynika to z faktu, że jest to system pozycyjny tak jak system dwójkowy). Aby obliczyć cyfrowe dopełnienie danej liczby wystarczy dla każdego iloczynu podmienić cyfrę z jej różnicą z liczbą 9. Każdą liczbę możemy wyrazić wzorem:

10⁰ * j + 10¹ * d + 10² * s + 10³ * t + … 10ⁿ * m

, gdzie j to cyfra jedności, d to cyfra dziesiątek, s to cyfra setek, t to cyfra tysięcy, n to ilość cyfr danej liczby pomniejszona o jeden, a m to najbardziej znacząca cyfra liczby (pierwsza z lewej). Z założenia z zadania wiemy, że m jest całkowite z przedziału (0, 9). Cyfrowe dopełnienie dla liczby z powyższego wzoru możemy więc zapisać w następujący sposób:

10⁰ * (9 – j) + 10¹ * (9 – d) + 10² * (9 – s) + 10³ * (9 – t) + … 10ⁿ * (9 – m)

Z wiedzą tą możemy przejść do rozwiązywania podpunktów.

Podpunkt 1

W podpunkcie tym proszą nas o wartość bezwzględną z różnicy liczby i jej cyfrowego dopełnienia. Wynika to z faktu, że odejmowana liczba może być większa od tej pierwszej. Oznacza to, że w dla każdego wariantu istnieją dwie poprawne odpowiedzi. Jak zatem możemy zapisać tą różnicę? Skorzystajmy z powyższego wzoru! Przyjmiemy j, d, s oraz t jako kolejne cyfry rozwinięcia dziesiętnego. Nasza wyjściowa liczba ma więc postać

j + 10d + 100s + 1000t

Uwaga: należy pamiętać, że t należy do całkowitych cyfr z przedziału <1, 8>, aby spełniał warunki z zadania. Pozostałe cyfry należą do całkowitych cyfr z przedziału <0, 9>. Różnicę liczby i jej cyfrowego dopełnienia możemy po uproszczeniu zapisać jako

2 * (j + 10d + 100s + 1000t) – 9999

Możemy przystąpić do obliczeń:

Aby wartość bezwzględna tej różnicy była możliwie jak najmniejsza, to iloczyn 2 * (j + 10d + 100s + 1000t) musi być możliwie jak najbliższy liczbie 9999. Zaokrąglimy więc liczbę 9999 w górę, aby dostać liczbę podzielną na dwa: 10000. Wiemy więc, że aby otrzymać 0 (najmniejszą możliwą wartość bezwzględną) to suma z nawiasu musi być równa 5000. Uwaga: można również zaokrąglić w dół do najbliższej liczby podzielnej przez dwa – wtedy dostaniemy liczbę 9998 i wynik 4999, który jest cyfrowym dopełnieniem pierwszego wyniku.
Aby wartość bezwzględna tej różnicy była możliwe jak największa, to suma (j + 10d + 100s + 1000t) musi być najmniejsza. Za każdą cyfrę wybieramy więc najmniejszą cyfrę z przedziału: j = 0, d = 0, s = 0, t = 1. Naszą n o najmniejszej różnicy z cyfrowym dopełnieniem jest więc 1000. Poprawnym wynikiem jest też 8999.

Uwaga: nie można było wpisać dwóch liczb – należy wybrać jedną z dwóch poprawnych odpowiedzi.

Podpunkt 2

W tegorocznym zadaniu z algorytmem CKE narzuciło dosyć sporo wymagań, przy jednoczesnym uszczupleniu dostępnych działań, nie można bowiem korzystać ze zmiennych innych niż typu całkowitego. To „utrudnienie” nasuwa nam jednak od razu sposób rozwiązania: wystarczy rozbić liczbę na cyfry poprzez cykliczne wykorzystanie operatora modulo i dzielenia całkowitego. Wykorzystamy w tym celu pętlę while, a także zmienną pomocniczą pom która będzie przechowywać aktualną potęgę liczby 10. W pętli obliczymy różnicę 9 – (n % 10), podzielimy liczbę n całkowicie przez 10 (pozbywamy się w ten sposób kolejnych cyfr), dodamy iloczyn obliczonej różnicy z pom do zmiennej d, a następnie pomnożymy liczbę pom przez 10. Całość będzie wykonywać się dopóki n będzie większa od zera. Algorytm ten możemy zapisać jako pseudokod:

pom = 1
d = 0
dopóki n > 0:
c = 9 – n%10
n = n div 10
d = d + c * pom
pom = pom * 10
wypisz d

Gdzie div to dzielnie całkowite, a % to operator obliczający resztę z dzielenia (modulo).

Matura z informatyki 2021 zadanie 2 – analiza algorytmu

Dosyć prosty algorytm, którego działanie polega kolejno na:

Dodaniu kolejnego elementu na koniec tablicy
Sprawdzaniu, czy ostatni element tablicy jest większy od elementu środkowego (element środkowy wskazuje zmienna pomocnicza). Jeżeli tak, to nastąpi podmiana tych elementów i dzielenie całkowite zmiennej pomocniczej przez dwa. Działania te będą powtarzane, do momentu, gdy zmienna będzie większa od zera i element na który ona wskazuje będzie większy od poprzednio wskazanego środka.

Powyższy algorytm możemy przedstawić w postaci schematu blokowego:

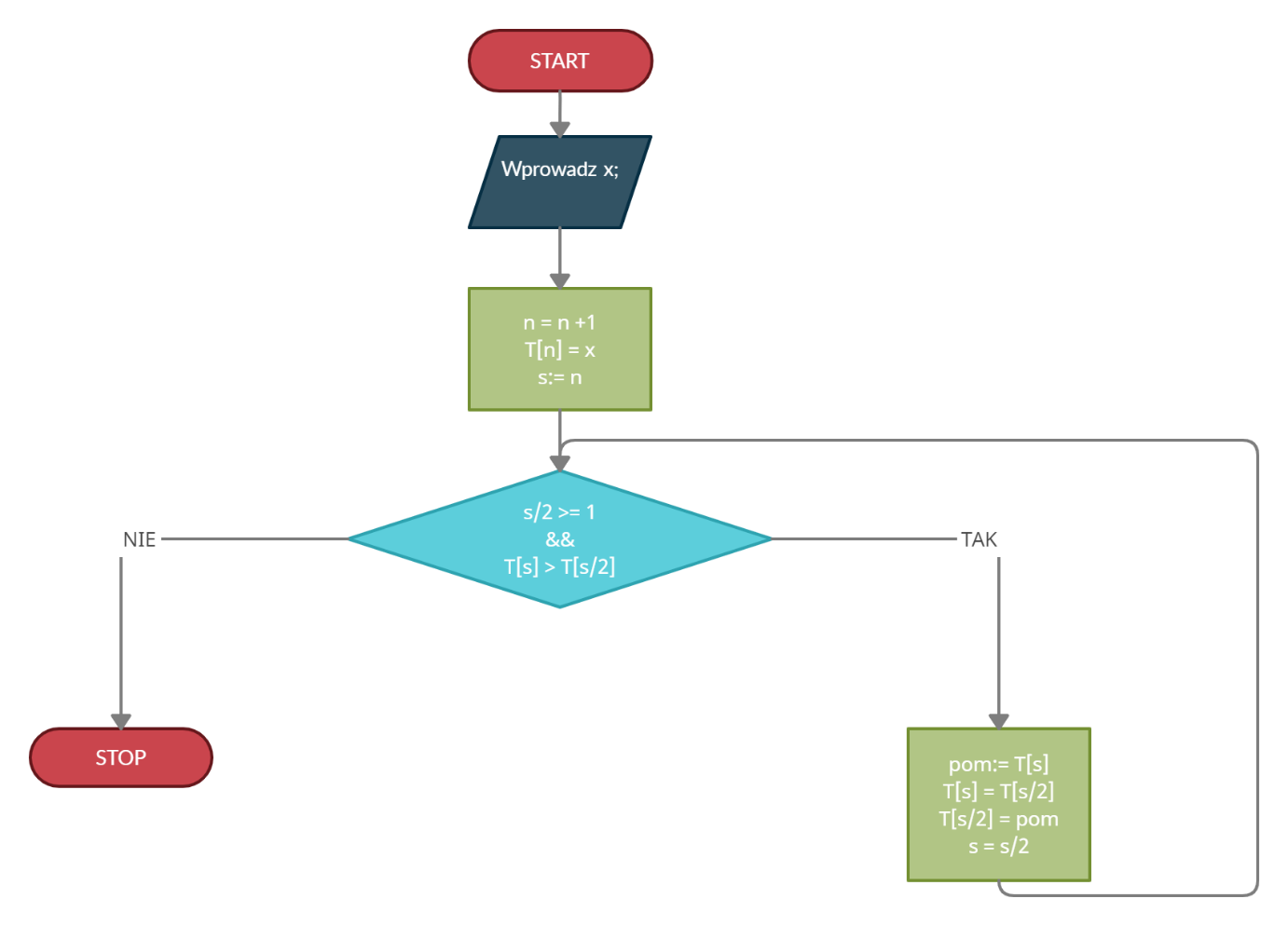
matura z informatyki 2021 zadanie 2 schemat blokowy

Pamiętajcie, że CKE w zadaniu tym rozpoczyna indeksowanie tablicy od jedynki, a nie od zera, jak to ma miejsce w większości języków programowania. Z wiedzą tą możemy przejść do rozwiązywania podpunktów:

Podpunkt 1

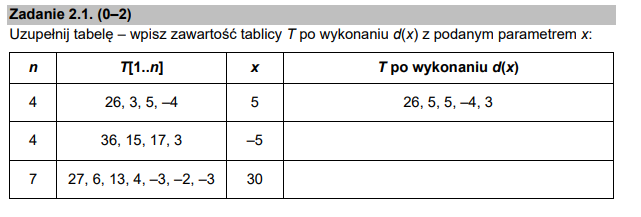
Nie pozostaje nam nic innego, jak „ręczne” przejście przez kolejne kroki algorytmu dla podanych wartości:

W pierwszym przypadku algorytm nawet nie rozpoczyna działania pętli: środkowy wyraz jest większy od ostatniego.

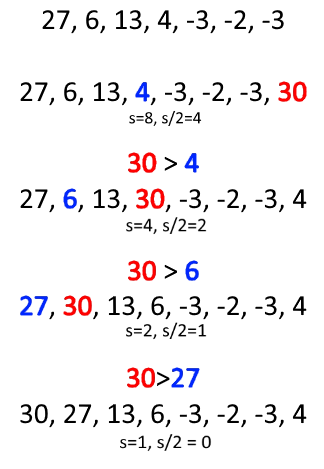
W kolejnym przypadku pętla wykona 3 iteracje. Liczba 30 była największa z podanego zbioru, więc logicznym było, że ostatecznie znajdzie się na początku, jednakże wiedza to nie jest wystarczająca, gdyż, jak zapewne zauważyliście, niektóre mniejsze elementy zbioru znajdują się w zupełnie innym miejscu. Tabela powinna być więc uzupełniona w następujący sposób:

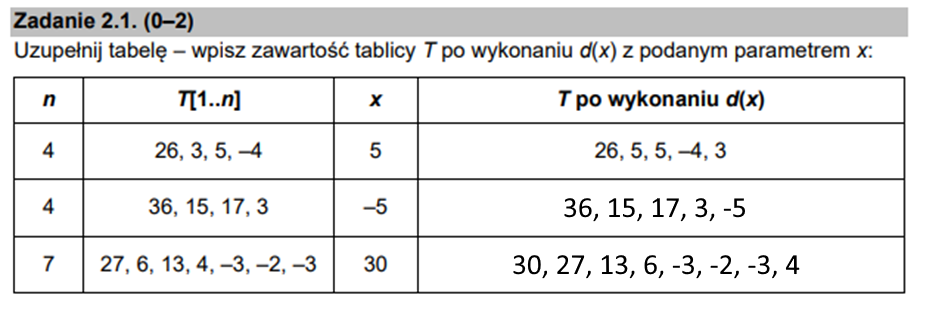
Podpunkt 2

Ten podpunkt rozwiązujemy również tak samo jak poprzedni:

d(6) – tablica jest pusta, więc dostawiamy tylko element 6, wynikiem jest więc [6]
d(-4) – argument jest mniejszy od szóstki, dostawiamy więc go tylko na koniec: [6, -4]
d(12) – argument jest większy od szóstki, podmieniamy je więc miejscem: [12, -4, 6]
d(27) – argument jest większy od -4, podmieniamy je więc miejscem: [12, 27, 6, -4]. 27 jest większe od 12, wiec je też podmieniamy: [27, 12, 6, -4]
d(26) – argument jest większy od 12, podmieniamy: [27, 26, 6, -4, 12]
d(8) – argument jest większy od szóstki, podmieniamy: [27, 26, 8, -4, 12, 6]

Odpowiedzią będzie więc poniższa tablica:

Podpunkt 3

W podpunkcie tym dokonamy szybkiej analizy. Do tablicy dodajemy coraz to większe liczby, co oznacza to, że dodana liczba zawsze zostanie wyrzucona na początek. W takim przypadku ilość wywołań warunku będzie zależna od wielkości całej tablicy. Ponieważ dzielimy rozpatrywany zakres tablicy co każdą iterację przez 2, to wystarczy sprawdzić ile razy dla danego k takie dzielenie nastąp. Sprawdzamy do momentu, w którym dostaniemy 0. W ten sposób dla k=4 mamy: 4 > 2 > 1 > 0, co daje 3 sprawdzenia – jest to zgodne z wytycznymi zadania. Dla k=16 mamy: 16 > 8 > 4 > 2 > 1 > 0, co daje 5 powtórzeń, a dla k=1025 mamy: 1025 > 512 > 256 > 128 > 64 > 32 > 16 > 8 > 4 > 2 > 1 > 0, co daje 11 powtórzeń :

Matura z informatyki 2021 zadanie 3 – zadania zamknięte

Kolejne zadanie, tak jak co roku, składa się z kilku zamkniętych podpunktów typu PRAWDA/FAŁSZ.

Podpunkt 1

Algorytm wypisuje wprowadzoną liczbę, a następnie wywołuje sam siebie dla liczby pomniejszonej o 2. Mamy więc do czynienia z funkcją rekurencyjną. Warunkiem zatrzymania jest sytuacja, w której argument funkcji jest niedodatni. Od razu możemy stwierdzić fałszywość punktu 1., bo wypisane zostały te same wartości, a także punkt 4., w którym wydrukowane zostały zera, co jest sprzeczne z warunkiem zatrzymania. Pozostałe punkty są prawdziwe, ponieważ widzimy symetryczność wypisanych danych, a także początkowy spadek, a następnie wzrost wartości o 2.

Podpunkt 2

W podpunkcie tym nie pozostaje nam nic innego jak prosta zamiana wartości na jeden system, a następnie ich porównanie. Zapiszmy więc każdą liczbę w systemie dziesiętnym:

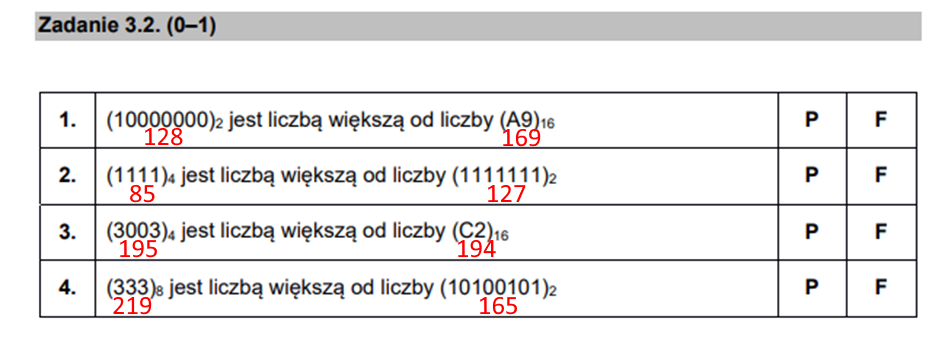
Po zamianie na czytelny dla nas system możemy udzielić odpowiedzi:

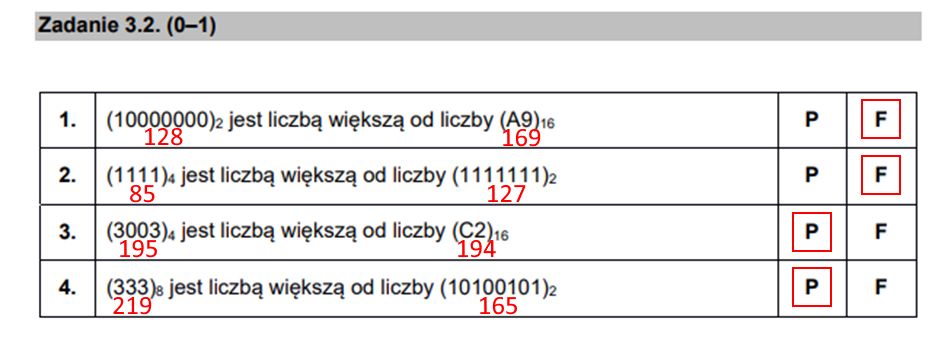
Podpunkt 3

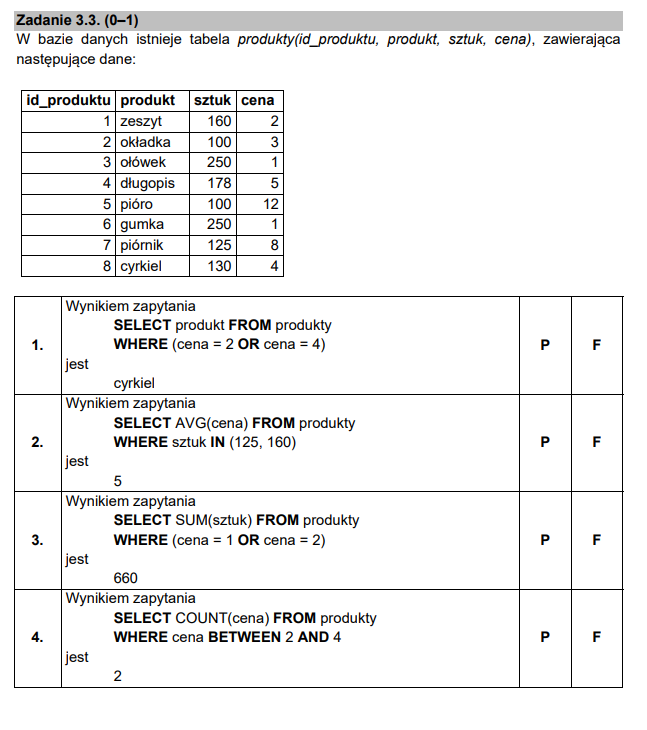
W zadaniach sprawdzających wiedzę z baz danych najprościej jest prześledzić jaki faktyczny wynik da dana kwerenda:

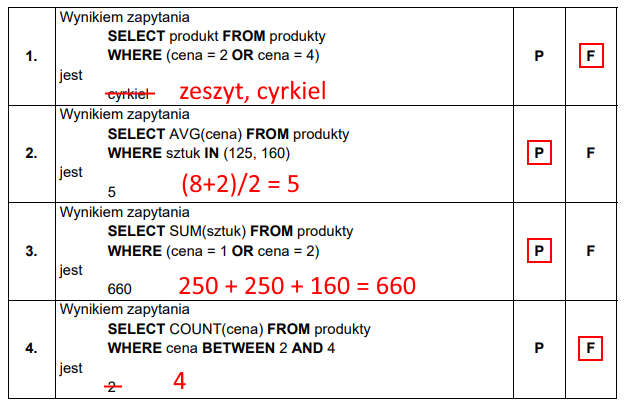
Wynik pierwszej kwerendy jest błędny, gdyż pomija ona drugi, pasujący do kryteriów wynik. Przy drugiej kwerendzie należało pamiętać, że sztuk IN(125, 160) jest odpowiednikiem WHERE (sztuk = 125 OR sztuk=160), co oznacza, że wybierane były jedynie rekordy, dla których ilość sztuk byłą równa 125 lub 160. Następnie należało obliczyć średnią cenę tych rekordów, czego wynikiem jest 5. Trzecia kwerenda sumowała po prostu ilość sztuk produktów, których cena jest równa jeden lub dwa, dając prawidłowy wynik 660. Ostatni haczyk jaki na nas czekał, to fakt, że BETWEEN rozpatruje wartości w przedziale domkniętym, przez co wynik czwartej kwerendy to nie 2, a 4.

Matura z informatyki 2021 – część druga

Przed nami kolejna, bardziej decydująca część tegorocznej matury z informatyki. To właśnie z niej możemy zdobyć aż 70% wyniku całego egzaminu. Jeżeli więc załamaliście się poznając odpowiedzi z części zamkniętej, to bez obaw – mieliście jeszcze szerokie pole do popisu na drugiej części matury. Klasycznie, jak co roku, dostajemy do dyspozycji kilka plików tekstowych, na podstawie których musimy udzielić odpowiedzi do zadań. Plik z danymi znajdziecie tutaj. Przejdźmy zatem do jej rozwiązywania:

Jeżeli po maturze nadal chcesz rozwijać swoje umiejętności, to polecamy usługi hostingowe **dhosting**, przy użyciu których podszlifujesz swoje umiejętności front i backendowe.

Matura z informatyki 2021 zadanie 4 – neon cyfrowy

Plik zawiera kolejne instrukcje dla tablicy neonowej wyświetlającej napisy. Najrozsądniejszym rozwiązaniem będzie stworzenie 4 różnych metod, które będą wykonywały opisane w poleceniu zadania. Następnie sczytamy zawartość pliku wiersz po wierszu i pobierzemy polecenie, a także dany znak. Kolejnym krokiem będzie wywołanie odpowiednich funkcji bazując na pobranej komendzie i znaku. Na koniec możemy wyświetlić finalny napis i zamknąć plik:

C++

#include &lt;iostream>
#include &lt;fstream>

using namespace std;

string dopisz(string text, const char &amp;c){ //funkcja dopisujaca podany znak
    return text + c;
}
string zmien(string text, const char &amp;c){ //funkcja zmieniajaca ostatni znak
    text[text.length()-1] = c;
    return text;
}
string usun(string text){ //funkcja usuwajaca ostatni znak
    text.pop_back();
    return text;
}
string przesun(string text, char &amp;c){ //funkcja przesuwajaca znak
    int t = text.find(c); //najpierw sprawdzamy, czy dany znak w ogole istnieje
    if(t != -1){ //jezeli tak
        if(c == 'Z'){//to najpierw sprawdzamy czy nie jest ostatnia litera alfabetu
            c = 'A'; //jezeli tak, to go przesuwamy
        }
        else{
            c++; //:) w przeciwnym przypadku zwiekszamy go o jeden (kolejny znak w tablicy ASCII)
        }
        text[t] = c; //podmieniamy nastepnie znak
    }
    return text;
}

int main()
{
    fstream input("C:\\dane-2021\\instrukcje.txt", fstream::in); //otwieramy nasz plik
    string napis = ""; //definujemy zmienna przechowujaca finalny napis
    if(!input){
        perror("Nie udalo sie otworzyc pliku");
        return 1;
    }
    string s; //zmienna przechowujaca aktualna komende/znak
    bool isCommand = true; //zmienna informujaca, czy aktualnie mamy doczynienia z komenda czy ze znakiem
    char currentChar = '0'; //zmienna przechowujaca aktualny znak w wierszu
    int command = -1; //zmienna przechowujaca aktualna komende wiersza
    while(input >> s){ //dopoki nie napotkamy konca pliku
        if(isCommand){ //sprawdzamy czy mamy doczynienia z komenda
            if(s == "DOPISZ"){ //jezeli tak to zapisujemy jej kod: 0 - dopisz, 1 - zmien, 2 - usun, 3 - przesun
                command = 0;
            }else if(s == "ZMIEN"){
                command = 1;
            }else if(s == "USUN"){
                command = 2;
            }else if(s == "PRZESUN"){
                command = 3;
            }
            isCommand = false; //przestawiamy zmienna pomocnicza - kolejna zczytana wartosc bedzie znakiem
        }
        else {
            currentChar = s[0]; //pobieramy aktualny znak
            switch(command){ //nastepnie wykonujemy odpowiednia komende wg zapisanego kodu
            case 0:
                napis = dopisz(napis, currentChar);
                break;
            case 1:
                napis = zmien(napis, currentChar);
                break;
            case 2:
                napis = usun(napis);
                break;
            case 3:
                napis = przesun(napis, currentChar);
                break;
            }
            isCommand = true; //przestawiamy zmienna pomocnicza - kolejna zczytana wartosc bedzie komenda
        }
    }
    input.close(); //zawsze należy zamknąć plik, gdy skończymy związane z nim prace
    cout &lt;&lt; napis; //drukujemy finalny napis
    return 0;
}

#include <iostream>

#include <fstream>

using namespace std;

string dopisz(string text, const char &c){ //funkcja dopisujaca podany znak

return text + c;

}

string zmien(string text, const char &c){ //funkcja zmieniajaca ostatni znak

text[text.length()-1] = c;

return text;

}

string usun(string text){ //funkcja usuwajaca ostatni znak

text.pop_back();

return text;

}

string przesun(string text, char &c){ //funkcja przesuwajaca znak

int t = text.find(c); //najpierw sprawdzamy, czy dany znak w ogole istnieje

if(t != -1){ //jezeli tak

if(c == 'Z'){//to najpierw sprawdzamy czy nie jest ostatnia litera alfabetu

c = 'A'; //jezeli tak, to go przesuwamy

}

else{

c++; //:) w przeciwnym przypadku zwiekszamy go o jeden (kolejny znak w tablicy ASCII)

}

text[t] = c; //podmieniamy nastepnie znak

}

return text;

}

int main()

{

fstream input("C:\\dane-2021\\instrukcje.txt", fstream::in); //otwieramy nasz plik

string napis = ""; //definujemy zmienna przechowujaca finalny napis

if(!input){

perror("Nie udalo sie otworzyc pliku");

return 1;

}

string s; //zmienna przechowujaca aktualna komende/znak

bool isCommand = true; //zmienna informujaca, czy aktualnie mamy doczynienia z komenda czy ze znakiem

char currentChar = '0'; //zmienna przechowujaca aktualny znak w wierszu

int command = -1; //zmienna przechowujaca aktualna komende wiersza

while(input >> s){ //dopoki nie napotkamy konca pliku

if(isCommand){ //sprawdzamy czy mamy doczynienia z komenda

if(s == "DOPISZ"){ //jezeli tak to zapisujemy jej kod: 0 - dopisz, 1 - zmien, 2 - usun, 3 - przesun

command = 0;

}else if(s == "ZMIEN"){

command = 1;

}else if(s == "USUN"){

command = 2;

}else if(s == "PRZESUN"){

command = 3;

}

isCommand = false; //przestawiamy zmienna pomocnicza - kolejna zczytana wartosc bedzie znakiem

}

else {

currentChar = s[0]; //pobieramy aktualny znak

switch(command){ //nastepnie wykonujemy odpowiednia komende wg zapisanego kodu

case 0:

napis = dopisz(napis, currentChar);

break;

case 1:

napis = zmien(napis, currentChar);

break;

case 2:

napis = usun(napis);

break;

case 3:

napis = przesun(napis, currentChar);

break;

}

isCommand = true; //przestawiamy zmienna pomocnicza - kolejna zczytana wartosc bedzie komenda

}

input.close(); //zawsze należy zamknąć plik, gdy skończymy związane z nim prace

cout << napis; //drukujemy finalny napis

return 0;

}

Java

ackage matura;

import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;

public class Zadanie4 {

	public static void main(String[] args) throws IOException {
		File f = new File("C:\\DANE_2105\\instrukcje.txt"); //ladujemy plik
		BufferedReader br = new BufferedReader(new FileReader(f)); //odczytujemy go za pomoca buffered readera
		String line = ""; //zmienna przechowujaca aktualny wiersz
		String result = ""; //zmienna przechowujaca wynik
		while((line = br.readLine()) != null) { //dopoki mamy co czytac
			String arg[] = line.split(" "); //zczytujemy linie i dzielimy ja na komende i znak
			String command = arg[0]; //pierwsza jest komenda
			char c = arg[1].charAt(0); //drugi znak
			if(command.equalsIgnoreCase("dopisz")) { //nastepnie rozpoznajemy typ komendy
				result = dopisz(result, c);
			}else if(command.equalsIgnoreCase("zmien")) { 
				result = zmien(result, c);
			}else if(command.equalsIgnoreCase("usun")) {
				result = usun(result);
			}
			else if(command.equalsIgnoreCase("przesun")) {
				result = przesun(result, c);
			}
		}
		br.close();
		System.out.println(result); //zwracamy wynik
	}
	
	static String dopisz(String txt, char c) { //funkcja dopisujaca znak na koncu tekstu
		return txt + c;
	}
	static String zmien(String txt, char c) { //funkcja podmieniajaca ostatni znak
		char[] chars = txt.toCharArray();
		chars[chars.length-1] = c;
		return new String(chars);
	}
	static String usun(String txt) { //funkcja usuwajaca ostatni znak
		return txt.substring(0, txt.length()-1);
	}
	static String przesun(String txt, char c) { //funkcja podmieniajaca pierwsze wystapienie znaku
		int t = txt.indexOf(c);
		if(t == - 1) {
			return txt;
		}
		if(c == 'Z') {
			c = 'A';
		}
		else {
			c++;
		}
		char[] chars = txt.toCharArray();
		chars[t] = c;
		return new String(chars);
	}
}

ackage matura;

import java.io.BufferedReader;

import java.io.File;

import java.io.FileReader;

import java.io.IOException;

public class Zadanie4 {

public static void main(String[] args) throws IOException {

File f = new File("C:\\DANE_2105\\instrukcje.txt"); //ladujemy plik

BufferedReader br = new BufferedReader(new FileReader(f)); //odczytujemy go za pomoca buffered readera

String line = ""; //zmienna przechowujaca aktualny wiersz

String result = ""; //zmienna przechowujaca wynik

while((line = br.readLine()) != null) { //dopoki mamy co czytac

String arg[] = line.split(" "); //zczytujemy linie i dzielimy ja na komende i znak

String command = arg[0]; //pierwsza jest komenda

char c = arg[1].charAt(0); //drugi znak

if(command.equalsIgnoreCase("dopisz")) { //nastepnie rozpoznajemy typ komendy

result = dopisz(result, c);

}else if(command.equalsIgnoreCase("zmien")) {

result = zmien(result, c);

}else if(command.equalsIgnoreCase("usun")) {

result = usun(result);

}

else if(command.equalsIgnoreCase("przesun")) {

result = przesun(result, c);

}

br.close();

System.out.println(result); //zwracamy wynik

}

static String dopisz(String txt, char c) { //funkcja dopisujaca znak na koncu tekstu

return txt + c;

}

static String zmien(String txt, char c) { //funkcja podmieniajaca ostatni znak

char[] chars = txt.toCharArray();

chars[chars.length-1] = c;

return new String(chars);

}

static String usun(String txt) { //funkcja usuwajaca ostatni znak

return txt.substring(0, txt.length()-1);

}

static String przesun(String txt, char c) { //funkcja podmieniajaca pierwsze wystapienie znaku

int t = txt.indexOf(c);

if(t == - 1) {

return txt;

}

if(c == 'Z') {

c = 'A';

}

else {

c++;

}

char[] chars = txt.toCharArray();

chars[t] = c;

return new String(chars);

}

Python

def dopisz(txt, c): #funkcja dopsisujaca znak
    return txt + c


def zmien(txt, c): #funckja zmieniajaca ostatni znak
    txtlist = list(txt) #uwaga: w pythonie teksty musimy potraktowac jako liste
    txtlist[len(txt)-1] = c #jezeli chcemy podmienic znak na danej pozycji
    return "".join(txtlist) #na koniec liste ta musimy zmienic z powrotem na tekst


def usun(txt): #funkcja usuwajaca ostatni znak
    return txt[:len(txt)-1]


def przesun(txt, c): #funkcja przesuwajaca znak o jedno miejsce w tablicy ASCII
    index = txt.find(c)
    if index == -1: #jezeli nie znalezlismy znaku, przerywamy dzialanie
        return txt
    if c == 'Z': #jezeli jest to ostatnia litera alfabetu, to wracamy na poczatek
        c = 'A'
    else: #w przeciwnym przypadku przesuwamy znak o 1
        c = chr(ord(c) + 1)
    txtlist = list(txt) #nastepnie musimy ponownie zamienic text na liste znakow
    txtlist[index] = c #podmienic znak
    return "".join(txtlist) #i zwrocic ja jako ciag znakow


file = open("C:\\DANE_2105\\instrukcje.txt", "r") #otwieramy plik w trybie read
result = "" #zmienna przechowujaca nasz wynik
for line in file: #iterujemy poprzez kazdy wiersz
    args = line.split(" ") #nastepnie dzielimy go na komende i znak
    char = args[1][0]#drugi jest znak
    command = args[0] #pierwsza komenda
    if command == "DOPISZ": #wywolujemy odpowiednie funkcje wg komendy
        result = dopisz(result, char)
    if command == "ZMIEN":
        result = zmien(result, char)
    if command == "USUN":
        result = usun(result)
    if command == "PRZESUN":
        result = przesun(result, char)
file.close() #na koniec musimy zamknac plik
print(result) #drukujemy wynik

def dopisz(txt, c): #funkcja dopsisujaca znak

return txt + c

def zmien(txt, c): #funckja zmieniajaca ostatni znak

txtlist = list(txt) #uwaga: w pythonie teksty musimy potraktowac jako liste

txtlist[len(txt)-1] = c #jezeli chcemy podmienic znak na danej pozycji

return "".join(txtlist) #na koniec liste ta musimy zmienic z powrotem na tekst

def usun(txt): #funkcja usuwajaca ostatni znak

return txt[:len(txt)-1]

def przesun(txt, c): #funkcja przesuwajaca znak o jedno miejsce w tablicy ASCII

index = txt.find(c)

if index == -1: #jezeli nie znalezlismy znaku, przerywamy dzialanie

return txt

if c == 'Z': #jezeli jest to ostatnia litera alfabetu, to wracamy na poczatek

c = 'A'

else: #w przeciwnym przypadku przesuwamy znak o 1

c = chr(ord(c) + 1)

txtlist = list(txt) #nastepnie musimy ponownie zamienic text na liste znakow

txtlist[index] = c #podmienic znak

return "".join(txtlist) #i zwrocic ja jako ciag znakow

file = open("C:\\DANE_2105\\instrukcje.txt", "r") #otwieramy plik w trybie read

result = "" #zmienna przechowujaca nasz wynik

for line in file: #iterujemy poprzez kazdy wiersz

args = line.split(" ") #nastepnie dzielimy go na komende i znak

char = args[1][0]#drugi jest znak

command = args[0] #pierwsza komenda

if command == "DOPISZ": #wywolujemy odpowiednie funkcje wg komendy

result = dopisz(result, char)

if command == "ZMIEN":

result = zmien(result, char)

if command == "USUN":

result = usun(result)

if command == "PRZESUN":

result = przesun(result, char)

file.close() #na koniec musimy zamknac plik

print(result) #drukujemy wynik

Mając już bazowy program możemy przejść do rozwiązywania podpunktów.

Podpunkt 1

Z racji, iż w naszym programie mamy już zbudowany napis według podanych instrukcji, to aby udzielić odpowiedzi na ten podpunkt wystarczy skorzystać z funkcji z typu string zwracającej długość napisu. W pliku bazowym wystarczy więc zmienić linijkę wypisującą tekst tak, aby wypisywała jego długość:

 cout&nbsp;&lt;&lt;&nbsp;napis.length();&nbsp;<em>//drukujemy</em>&nbsp;<em>dlugosc napisu</em>

1	cout << napis.length(); <em>//drukujemy</em> <em>dlugosc napisu</em>

System.out.println(result.length); //drukujemy dlugosc napisu

1	System.out.println(result.length); //drukujemy dlugosc napisu

print(len(result)) #drukujemy dlugosc napisu

1	print(len(result)) #drukujemy dlugosc napisu

Po uruchomieniu powyższych programów uzyskujemy odpowiedź: długość napisu jest równa 517.

Podpunkt 2

Podpunkt ten wymaga od nas już nieco więcej pracy. y zmodyfikować główny kod programu, aby zliczał ilość instrukcji wywołanych pod rząd. Musimy również przechować długość najdłuższego ciągu, a także komendę, jaka była w nim wywołana. Gdy wykryjemy przerwanie ciągu (czyli sczytamy nową komendę), to wtedy sprawdzimy, czy długość aktualnego ciągu jest większa od przechowanego najdłuższego. Jeżeli aktualny ciąg będzie dłuższy, to ustawiamy go jako nowy, najdłuższy ciąg.

C++

#include &lt;iostream>
#include &lt;fstream>

using namespace std;

string dopisz(string text, const char &amp;c){ //funkcja dopisujaca podany znak
    return text + c;
}
string zmien(string text, const char &amp;c){ //funkcja zmieniajaca ostatni znak
    text[text.length()-1] = c;
    return text;
}
string usun(string text){ //funkcja usuwajaca ostatni znak
    text.pop_back();
    return text;
}
string przesun(string text, char &amp;c){ //funkcja przesuwajaca znak
    int t = text.find(c); //najpierw sprawdzamy, czy dany znak w ogole istnieje
    if(t != -1){ //jezeli tak
        if(c == 'Z'){//to najpierw sprawdzamy czy nie jest ostatnia litera alfabetu
            c = 'A'; //jezeli tak, to go przesuwamy
        }
        else{
            c++; //:) w przeciwnym przypadku zwiekszamy go o jeden (kolejny znak w tablicy ASCII)
        }
        text[t] = c; //podmieniamy nastepnie znak
    }
    return text;
}

int main()
{
    fstream input("C:\\dane-2021\\instrukcje.txt", fstream::in); //otwieramy nasz plik
    string napis = ""; //definujemy zmienna przechowujaca finalny napis
    if(!input){
        perror("Nie udalo sie otworzyc pliku");
        return 1;
    }
    string s; //zmienna przechowujaca aktualna komende/znak
    bool isCommand = true; //zmienna informujaca, czy aktualnie mamy doczynienia z komenda czy ze znakiem
    char currentChar = '0'; //zmienna przechowujaca aktualny znak w wierszu
    int command = -1; //zmienna przechowujaca aktualna komende wiersza
    int maxCommand = -1; //zmienna przechowujaca kod komendy z najdluzszego ciagu
    int maxLength = -1; //zmienna przechowujaca dlugosc najdluzszego ciagu
    int currLength = 0; //zmienna przechowujaca kod komendy z aktualnego ciagu
    int currCommand = -1; //zmienna przechowujaca dlugosc aktualnego ciagu
    while(input >> s){ //dopoki nie napotkamy konca pliku
        if(isCommand){ //sprawdzamy czy mamy doczynienia z komenda
            if(s == "DOPISZ"){ //jezeli tak to zapisujemy jej kod: 0 - dopisz, 1 - zmien, 2 - usun, 3 - przesun
                command = 0;
            }else if(s == "ZMIEN"){
                command = 1;
            }else if(s == "USUN"){
                command = 2;
            }else if(s == "PRZESUN"){
                command = 3;
            }
            if(currCommand == -1){ //jezeli nie mamy jeszcze kodu komendy
                currCommand = command; //ustawiamy aktualna komende
                currLength = 1; //a takze dlugosc ciagu na 1 (bo mamy juz jeden kod)
            }else if(currCommand != command){ //jezeli natrafimy na koniec ciagu(nowa komende)
                if(maxLength &lt; currLength){ //sprawdzamy czy ciag byl dluzszy od najwiekszego
                    maxLength = currLength; //jezeli tak, to ustawiamy go jako nowy najdluzszy
                    maxCommand = currCommand;
                }
                currLength = 1; //resetujemy aktualny ciag
                currCommand = command;
            }
            else {
                currLength++; //jezeli komenda jest taka sama, to zwiekszamy licznik
            }
            isCommand = false; //przestawiamy zmienna pomocnicza - kolejna zczytana wartosc bedzie znakiem
        }
        else {
            currentChar = s[0]; //pobieramy aktualny znak
            switch(command){ //nastepnie wykonujemy odpowiednia komende wg zapisanego kodu
            case 0:
                napis = dopisz(napis, currentChar);
                break;
            case 1:
                napis = zmien(napis, currentChar);
                break;
            case 2:
                napis = usun(napis);
                break;
            case 3:
                napis = przesun(napis, currentChar);
                break;
            }
            isCommand = true; //przestawiamy zmienna pomocnicza - kolejna zczytana wartosc bedzie komenda
        }
    }
    input.close(); //zawsze należy zamknąć plik, gdy skończymy związane z nim prace
    string commands[] = {"DOPISZ", "ZMIEN", "USUN", "PRZESUN"}; //zmienna pomocnicza przechowujaca nazwy komend

    cout &lt;&lt; commands[maxCommand] &lt;&lt; " " &lt;&lt; maxLength &lt;&lt; endl; //wypisujemy nazwe komendy, a takze dlugosc najdluzszego ciagu
    return 0;
}

#include <iostream>

#include <fstream>

using namespace std;

string dopisz(string text, const char &c){ //funkcja dopisujaca podany znak

return text + c;

}

string zmien(string text, const char &c){ //funkcja zmieniajaca ostatni znak

text[text.length()-1] = c;

return text;

}

string usun(string text){ //funkcja usuwajaca ostatni znak

text.pop_back();

return text;

}

string przesun(string text, char &c){ //funkcja przesuwajaca znak

int t = text.find(c); //najpierw sprawdzamy, czy dany znak w ogole istnieje

if(t != -1){ //jezeli tak

if(c == 'Z'){//to najpierw sprawdzamy czy nie jest ostatnia litera alfabetu

c = 'A'; //jezeli tak, to go przesuwamy

}

else{

c++; //:) w przeciwnym przypadku zwiekszamy go o jeden (kolejny znak w tablicy ASCII)

}

text[t] = c; //podmieniamy nastepnie znak

}

return text;

}

int main()

{

fstream input("C:\\dane-2021\\instrukcje.txt", fstream::in); //otwieramy nasz plik

string napis = ""; //definujemy zmienna przechowujaca finalny napis

if(!input){

perror("Nie udalo sie otworzyc pliku");

return 1;

}

string s; //zmienna przechowujaca aktualna komende/znak

bool isCommand = true; //zmienna informujaca, czy aktualnie mamy doczynienia z komenda czy ze znakiem

char currentChar = '0'; //zmienna przechowujaca aktualny znak w wierszu

int command = -1; //zmienna przechowujaca aktualna komende wiersza

int maxCommand = -1; //zmienna przechowujaca kod komendy z najdluzszego ciagu

int maxLength = -1; //zmienna przechowujaca dlugosc najdluzszego ciagu

int currLength = 0; //zmienna przechowujaca kod komendy z aktualnego ciagu

int currCommand = -1; //zmienna przechowujaca dlugosc aktualnego ciagu

while(input >> s){ //dopoki nie napotkamy konca pliku

if(isCommand){ //sprawdzamy czy mamy doczynienia z komenda

if(s == "DOPISZ"){ //jezeli tak to zapisujemy jej kod: 0 - dopisz, 1 - zmien, 2 - usun, 3 - przesun

command = 0;

}else if(s == "ZMIEN"){

command = 1;

}else if(s == "USUN"){

command = 2;

}else if(s == "PRZESUN"){

command = 3;

}

if(currCommand == -1){ //jezeli nie mamy jeszcze kodu komendy

currCommand = command; //ustawiamy aktualna komende

currLength = 1; //a takze dlugosc ciagu na 1 (bo mamy juz jeden kod)

}else if(currCommand != command){ //jezeli natrafimy na koniec ciagu(nowa komende)

if(maxLength < currLength){ //sprawdzamy czy ciag byl dluzszy od najwiekszego

maxLength = currLength; //jezeli tak, to ustawiamy go jako nowy najdluzszy

maxCommand = currCommand;

}

currLength = 1; //resetujemy aktualny ciag

currCommand = command;

}

else {

currLength++; //jezeli komenda jest taka sama, to zwiekszamy licznik

}

isCommand = false; //przestawiamy zmienna pomocnicza - kolejna zczytana wartosc bedzie znakiem

}

else {

currentChar = s[0]; //pobieramy aktualny znak

switch(command){ //nastepnie wykonujemy odpowiednia komende wg zapisanego kodu

case 0:

napis = dopisz(napis, currentChar);

break;

case 1:

napis = zmien(napis, currentChar);

break;

case 2:

napis = usun(napis);

break;

case 3:

napis = przesun(napis, currentChar);

break;

}

isCommand = true; //przestawiamy zmienna pomocnicza - kolejna zczytana wartosc bedzie komenda

}

input.close(); //zawsze należy zamknąć plik, gdy skończymy związane z nim prace

string commands[] = {"DOPISZ", "ZMIEN", "USUN", "PRZESUN"}; //zmienna pomocnicza przechowujaca nazwy komend

cout << commands[maxCommand] << " " << maxLength << endl; //wypisujemy nazwe komendy, a takze dlugosc najdluzszego ciagu

return 0;

}

Java

package matura;

import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;

public class Podpunkt2 {

	public static void main(String[] args) throws IOException {
		File f = new File("C:\\DANE_2105\\instrukcje.txt"); //ladujemy plik
		BufferedReader br = new BufferedReader(new FileReader(f)); //odczytujemy go za pomoca buffered readera
		String line = ""; //zmienna przechowujaca aktualny wiersz
		String result = ""; //zmienna przechowujaca wynik
		int max = -1; //zmienna przechowujaca dlugosc najdluzszego ciagu
		String commandMax = ""; //zmienna przechowujaca komende najdluzszego ciagu
		String currentCommand = ""; //zmienna przechowujaca komende z aktualnego ciagu
		int currentLength = 0; //zmienna przechowujaca dlugosc aktualnego ciagu
		while((line = br.readLine()) != null) { //dopoki mamy co czytac
			String arg[] = line.split(" "); //zczytujemy linie i dzielimy ja na komende i znak
			String command = arg[0]; //pierwsza jest komenda
			char c = arg[1].charAt(0); //drugi znak
			if(currentCommand.isEmpty()) { //jezeli nie mamy jeszcze komendy, to pobieramy pierwsza
				currentCommand = command;
			}
			if (!currentCommand.equals(command)) { //jezeli komenda rozni sie od poprzedniej (koniec ciągu)
				if(max &lt; currentLength) { //jezeli dlugosc ciagu jest wieksza od dlugosci najdluzszego
					max = currentLength; //podmieniamy wartosci zmiennych
					commandMax = currentCommand;
				}
				currentCommand = command; //resetujemy zmienne, ustawiajac aktualna komende i dlugosc ciagu
				currentLength = 1;
			}
			else {
				currentLength++; //jezeli komenda jest taka sama to zwiekszamy licznik
			}
			if(command.equalsIgnoreCase("dopisz")) { //nastepnie rozpoznajemy typ komendy
				result = dopisz(result, c);
			}else if(command.equalsIgnoreCase("zmien")) { 
				result = zmien(result, c);
			}else if(command.equalsIgnoreCase("usun")) {
				result = usun(result);
			}
			else if(command.equalsIgnoreCase("przesun")) {
				result = przesun(result, c);
			}
		}
		br.close();
		System.out.println(commandMax + " " + max); //zwracamy wynik
	}
	
	static String dopisz(String txt, char c) { //funkcja dopisujaca znak na koncu tekstu
		return txt + c;
	}
	static String zmien(String txt, char c) { //funkcja podmieniajaca ostatni znak
		char[] chars = txt.toCharArray();
		chars[chars.length-1] = c;
		return new String(chars);
	}
	static String usun(String txt) { //funkcja usuwajaca ostatni znak
		return txt.substring(0, txt.length()-1);
	}
	static String przesun(String txt, char c) { //funkcja podmieniajaca pierwsze wystapienie znaku
		int t = txt.indexOf(c);
		if(t == - 1) {
			return txt;
		}
		if(c == 'Z') {
			c = 'A';
		}
		else {
			c++;
		}
		char[] chars = txt.toCharArray();
		chars[t] = c;
		return new String(chars);
	}
}

package matura;

import java.io.BufferedReader;

import java.io.File;

import java.io.FileReader;

import java.io.IOException;

public class Podpunkt2 {

public static void main(String[] args) throws IOException {

File f = new File("C:\\DANE_2105\\instrukcje.txt"); //ladujemy plik

BufferedReader br = new BufferedReader(new FileReader(f)); //odczytujemy go za pomoca buffered readera

String line = ""; //zmienna przechowujaca aktualny wiersz

String result = ""; //zmienna przechowujaca wynik

int max = -1; //zmienna przechowujaca dlugosc najdluzszego ciagu

String commandMax = ""; //zmienna przechowujaca komende najdluzszego ciagu

String currentCommand = ""; //zmienna przechowujaca komende z aktualnego ciagu

int currentLength = 0; //zmienna przechowujaca dlugosc aktualnego ciagu

while((line = br.readLine()) != null) { //dopoki mamy co czytac

String arg[] = line.split(" "); //zczytujemy linie i dzielimy ja na komende i znak

String command = arg[0]; //pierwsza jest komenda

char c = arg[1].charAt(0); //drugi znak

if(currentCommand.isEmpty()) { //jezeli nie mamy jeszcze komendy, to pobieramy pierwsza

currentCommand = command;

}

if (!currentCommand.equals(command)) { //jezeli komenda rozni sie od poprzedniej (koniec ciągu)

if(max < currentLength) { //jezeli dlugosc ciagu jest wieksza od dlugosci najdluzszego

max = currentLength; //podmieniamy wartosci zmiennych

commandMax = currentCommand;

}

currentCommand = command; //resetujemy zmienne, ustawiajac aktualna komende i dlugosc ciagu

currentLength = 1;

}

else {

currentLength++; //jezeli komenda jest taka sama to zwiekszamy licznik

}

if(command.equalsIgnoreCase("dopisz")) { //nastepnie rozpoznajemy typ komendy

result = dopisz(result, c);

}else if(command.equalsIgnoreCase("zmien")) {

result = zmien(result, c);

}else if(command.equalsIgnoreCase("usun")) {

result = usun(result);

}

else if(command.equalsIgnoreCase("przesun")) {

result = przesun(result, c);

}

br.close();

System.out.println(commandMax + " " + max); //zwracamy wynik

}

static String dopisz(String txt, char c) { //funkcja dopisujaca znak na koncu tekstu

return txt + c;

}

static String zmien(String txt, char c) { //funkcja podmieniajaca ostatni znak

char[] chars = txt.toCharArray();

chars[chars.length-1] = c;

return new String(chars);

}

static String usun(String txt) { //funkcja usuwajaca ostatni znak

return txt.substring(0, txt.length()-1);

}

static String przesun(String txt, char c) { //funkcja podmieniajaca pierwsze wystapienie znaku

int t = txt.indexOf(c);

if(t == - 1) {

return txt;

}

if(c == 'Z') {

c = 'A';

}

else {

c++;

}

char[] chars = txt.toCharArray();

chars[t] = c;

return new String(chars);

}

Python

def dopisz(txt, c): #funkcja dopsisujaca znak
    return txt + c


def zmien(txt, c): #funkcja zmieniajaca ostatni znak
    txtlist = list(txt) #uwaga: w pythonie teksty musimy potraktowac jako liste
    txtlist[len(txt)-1] = c #jezeli chcemy podmienic znak na danej pozycji
    return "".join(txtlist) #na koniec liste ta musimy zmienic z powrotem na tekst


def usun(txt): #funkcja usuwajaca ostatni znak
    return txt[:len(txt)-1]


def przesun(txt, c): #funkcja przesuwajaca znak o jedno miejsce w tablicy ASCII
    index = txt.find(c)
    if index == -1: #jezeli nie znalezlismy znaku, przerywamy dzialanie
        return txt
    if c == 'Z': #jezeli jest to ostatnia litera alfabetu, to wracamy na poczatek
        c = 'A'
    else: #w przeciwnym przypadku przesuwamy znak o 1
        c = chr(ord(c) + 1)
    txtlist = list(txt) #nastepnie musimy ponownie zamienic text na liste znakow
    txtlist[index] = c #podmienic znak
    return "".join(txtlist) #i zwrocic ja jako ciag znakow


file = open("C:\\DANE_2105\\instrukcje.txt", "r") #otwieramy plik w trybie read
result = "" #zmienna przechowujaca nasz wynik
max = -1 #zmienna przechowujaca najdluzsza dlugosc ciagu
maxc = "" #zmienna przechowujaca komende z najdluzszego ciagu
current = 0 #zmienna przechowujaca aktualna dlugosc ciagu
currentc = "" #zmienna przechowujaca aktualna komende z ciagu
for line in file: #iterujemy poprzez kazdy wiersz
    args = line.split(" ") #nastepnie dzielimy go na komende i znak
    char = args[1][0]#drugi jest znak
    command = args[0] #pierwsza komenda
    if command == "DOPISZ": #wywolujemy odpowiednie funkcje wg komendy
        result = dopisz(result, char)
    if command == "ZMIEN":
        result = zmien(result, char)
    if command == "USUN":
        result = usun(result)
    if command == "PRZESUN":
        result = przesun(result, char)
    if currentc == "": #jezeli nie mamy jeszcze komendy
        currentc = command #ustawiamy ta aktualna
        current = 1 #i ustaiwamy dlugosc ciagu na 1
    else:
        if currentc == command: #jezeli poprzednia komenda byla taka sama
            current += 1 #to zwiekszamy dlugosc ciagu o 1
        else: #w przeciwnym wypadku
            if max &lt; current: #sprawdzamy, czy aktualna dlugosc ciagu jest wieksza niz maksymalna
                max = current #jezeli tak to ustawiamy aktualny ciag jako najdluzszy
                maxc = currentc
            current = 1 #musimy jeszcze zresetowac wartosci ciagu; ustawiamy dlugosc na 1 (bo mamy juz pierwsza komende)
            currentc = command #a takze ustawiamy aktualna komende

file.close() #na koniec musimy zamknac plik
print(max, " ", maxc) #drukujemy wynik

def dopisz(txt, c): #funkcja dopsisujaca znak

return txt + c

def zmien(txt, c): #funkcja zmieniajaca ostatni znak

txtlist = list(txt) #uwaga: w pythonie teksty musimy potraktowac jako liste

txtlist[len(txt)-1] = c #jezeli chcemy podmienic znak na danej pozycji

return "".join(txtlist) #na koniec liste ta musimy zmienic z powrotem na tekst

def usun(txt): #funkcja usuwajaca ostatni znak

return txt[:len(txt)-1]

def przesun(txt, c): #funkcja przesuwajaca znak o jedno miejsce w tablicy ASCII

index = txt.find(c)

if index == -1: #jezeli nie znalezlismy znaku, przerywamy dzialanie

return txt

if c == 'Z': #jezeli jest to ostatnia litera alfabetu, to wracamy na poczatek

c = 'A'

else: #w przeciwnym przypadku przesuwamy znak o 1

c = chr(ord(c) + 1)

txtlist = list(txt) #nastepnie musimy ponownie zamienic text na liste znakow

txtlist[index] = c #podmienic znak

return "".join(txtlist) #i zwrocic ja jako ciag znakow

file = open("C:\\DANE_2105\\instrukcje.txt", "r") #otwieramy plik w trybie read

result = "" #zmienna przechowujaca nasz wynik

max = -1 #zmienna przechowujaca najdluzsza dlugosc ciagu

maxc = "" #zmienna przechowujaca komende z najdluzszego ciagu

current = 0 #zmienna przechowujaca aktualna dlugosc ciagu

currentc = "" #zmienna przechowujaca aktualna komende z ciagu

for line in file: #iterujemy poprzez kazdy wiersz

args = line.split(" ") #nastepnie dzielimy go na komende i znak

char = args[1][0]#drugi jest znak

command = args[0] #pierwsza komenda

if command == "DOPISZ": #wywolujemy odpowiednie funkcje wg komendy

result = dopisz(result, char)

if command == "ZMIEN":

result = zmien(result, char)

if command == "USUN":

result = usun(result)

if command == "PRZESUN":

result = przesun(result, char)

if currentc == "": #jezeli nie mamy jeszcze komendy

currentc = command #ustawiamy ta aktualna

current = 1 #i ustaiwamy dlugosc ciagu na 1

else:

if currentc == command: #jezeli poprzednia komenda byla taka sama

current += 1 #to zwiekszamy dlugosc ciagu o 1

else: #w przeciwnym wypadku

if max < current: #sprawdzamy, czy aktualna dlugosc ciagu jest wieksza niz maksymalna

max = current #jezeli tak to ustawiamy aktualny ciag jako najdluzszy

maxc = currentc

current = 1 #musimy jeszcze zresetowac wartosci ciagu; ustawiamy dlugosc na 1 (bo mamy juz pierwsza komende)

currentc = command #a takze ustawiamy aktualna komende

file.close() #na koniec musimy zamknac plik

print(max, " ", maxc) #drukujemy wynik

Powyższe programy generują odpowiedź ZMIEŃ 7.

Podpunkt 3

W tym podpunkcie wprowadzimy modyfikacje w miejscu, w którym wywołujemy funkcję dopisz. Stworzymy obiekt typu mapy, w którym połączymy znaki z ich ilością wystąpień. Następnie przeiterujemy tą mapę i wybierzemy tą najczęściej występującą.

C++

#include &lt;iostream>
#include &lt;fstream>
#include &lt;map> //wymagany include !!!

using namespace std;

string dopisz(string text, const char &amp;c){ //funkcja dopisujaca podany znak
    return text + c;
}
string zmien(string text, const char &amp;c){ //funkcja zmieniajaca ostatni znak
    text[text.length()-1] = c;
    return text;
}
string usun(string text){ //funkcja usuwajaca ostatni znak
    text.pop_back();
    return text;
}
string przesun(string text, char &amp;c){ //funkcja przesuwajaca znak
    int t = text.find(c); //najpierw sprawdzamy, czy dany znak w ogole istnieje
    if(t != -1){ //jezeli tak
        if(c == 'Z'){//to najpierw sprawdzamy czy nie jest ostatnia litera alfabetu
            c = 'A'; //jezeli tak, to go przesuwamy
        }
        else{
            c++; //:) w przeciwnym przypadku zwiekszamy go o jeden (kolejny znak w tablicy ASCII)
        }
        text[t] = c; //podmieniamy nastepnie znak
    }
    return text;
}

int main()
{
    fstream input("C:\\dane-2021\\instrukcje.txt", fstream::in); //otwieramy nasz plik
    string napis = ""; //definujemy zmienna przechowujaca finalny napis
    if(!input){
        perror("Nie udalo sie otworzyc pliku");
        return 1;
    }
    string s; //zmienna przechowujaca aktualna komende/znak
    bool isCommand = true; //zmienna informujaca, czy aktualnie mamy doczynienia z komenda czy ze znakiem
    char currentChar = '0'; //zmienna przechowujaca aktualny znak w wierszu
    int command = -1; //zmienna przechowujaca aktualna komende wiersza
    map&lt;char, int> charMap; //zmienna przechowujaca znaki i ich ilosc wystapien
    while(input >> s){ //dopoki nie napotkamy konca pliku
        if(isCommand){ //sprawdzamy czy mamy doczynienia z komenda
            if(s == "DOPISZ"){ //jezeli tak to zapisujemy jej kod: 0 - dopisz, 1 - zmien, 2 - usun, 3 - przesun
                command = 0;
            }else if(s == "ZMIEN"){
                command = 1;
            }else if(s == "USUN"){
                command = 2;
            }else if(s == "PRZESUN"){
                command = 3;
            }
            isCommand = false; //przestawiamy zmienna pomocnicza - kolejna zczytana wartosc bedzie znakiem
        }
        else {
            currentChar = s[0]; //pobieramy aktualny znak
            switch(command){ //nastepnie wykonujemy odpowiednia komende wg zapisanego kodu
            case 0:
                napis = dopisz(napis, currentChar);
                if(charMap.find(currentChar) != charMap.end()){ //jezeli mapa zawiera juz aktualny znak
                    charMap[currentChar]++; //zwiekszamy licznik wystapien o jeden
                }else {
                    charMap[currentChar] = 1; //w przeciwnym wypadku inicjalizujemy jego licznik zaczynajac od 1
                }
                break;
            case 1:
                napis = zmien(napis, currentChar);
                break;
            case 2:
                napis = usun(napis);
                break;
            case 3:
                napis = przesun(napis, currentChar);
                break;
            }
            isCommand = true; //przestawiamy zmienna pomocnicza - kolejna zczytana wartosc bedzie komenda
        }
    }
    input.close(); //zawsze należy zamknąć plik, gdy skończymy związane z nim prace
    int max = -1;
    char maxC = '0';
    for(auto a : charMap){
        if(a.second > max){
            maxC = a.first;
            max = a.second;
        }
    }
    cout &lt;&lt; maxC &lt;&lt; " " &lt;&lt; max &lt;&lt; " razy." &lt;&lt; endl;
    return 0;
}

#include <iostream>

#include <fstream>

#include <map> //wymagany include !!!

using namespace std;

string dopisz(string text, const char &c){ //funkcja dopisujaca podany znak

return text + c;

}

string zmien(string text, const char &c){ //funkcja zmieniajaca ostatni znak

text[text.length()-1] = c;

return text;

}

string usun(string text){ //funkcja usuwajaca ostatni znak

text.pop_back();

return text;

}

string przesun(string text, char &c){ //funkcja przesuwajaca znak

int t = text.find(c); //najpierw sprawdzamy, czy dany znak w ogole istnieje

if(t != -1){ //jezeli tak

if(c == 'Z'){//to najpierw sprawdzamy czy nie jest ostatnia litera alfabetu

c = 'A'; //jezeli tak, to go przesuwamy

}

else{

c++; //:) w przeciwnym przypadku zwiekszamy go o jeden (kolejny znak w tablicy ASCII)

}

text[t] = c; //podmieniamy nastepnie znak

}

return text;

}

int main()

{

fstream input("C:\\dane-2021\\instrukcje.txt", fstream::in); //otwieramy nasz plik

string napis = ""; //definujemy zmienna przechowujaca finalny napis

if(!input){

perror("Nie udalo sie otworzyc pliku");

return 1;

}

string s; //zmienna przechowujaca aktualna komende/znak

bool isCommand = true; //zmienna informujaca, czy aktualnie mamy doczynienia z komenda czy ze znakiem

char currentChar = '0'; //zmienna przechowujaca aktualny znak w wierszu

int command = -1; //zmienna przechowujaca aktualna komende wiersza

map<char, int> charMap; //zmienna przechowujaca znaki i ich ilosc wystapien

while(input >> s){ //dopoki nie napotkamy konca pliku

if(isCommand){ //sprawdzamy czy mamy doczynienia z komenda

if(s == "DOPISZ"){ //jezeli tak to zapisujemy jej kod: 0 - dopisz, 1 - zmien, 2 - usun, 3 - przesun

command = 0;

}else if(s == "ZMIEN"){

command = 1;

}else if(s == "USUN"){

command = 2;

}else if(s == "PRZESUN"){

command = 3;

}

isCommand = false; //przestawiamy zmienna pomocnicza - kolejna zczytana wartosc bedzie znakiem

}

else {

currentChar = s[0]; //pobieramy aktualny znak

switch(command){ //nastepnie wykonujemy odpowiednia komende wg zapisanego kodu

case 0:

napis = dopisz(napis, currentChar);

if(charMap.find(currentChar) != charMap.end()){ //jezeli mapa zawiera juz aktualny znak

charMap[currentChar]++; //zwiekszamy licznik wystapien o jeden

}else {

charMap[currentChar] = 1; //w przeciwnym wypadku inicjalizujemy jego licznik zaczynajac od 1

}

break;

case 1:

napis = zmien(napis, currentChar);

break;

case 2:

napis = usun(napis);

break;

case 3:

napis = przesun(napis, currentChar);

break;

}

isCommand = true; //przestawiamy zmienna pomocnicza - kolejna zczytana wartosc bedzie komenda

}

input.close(); //zawsze należy zamknąć plik, gdy skończymy związane z nim prace

int max = -1;

char maxC = '0';

for(auto a : charMap){

if(a.second > max){

maxC = a.first;

max = a.second;

}

cout << maxC << " " << max << " razy." << endl;

return 0;

}

Java

package matura;

import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;
import java.util.HashMap;

public class Podpunkt3 {

	public static void main(String[] args) throws IOException {
		File f = new File("C:\\DANE_2105\\instrukcje.txt"); //ladujemy plik
		BufferedReader br = new BufferedReader(new FileReader(f)); //odczytujemy go za pomoca buffered readera
		String line = ""; //zmienna przechowujaca aktualny wiersz
		String result = ""; //zmienna przechowujaca wynik
		HashMap&lt;Character, Integer> counter = new HashMap&lt;Character, Integer>(); //tworzymy zmienna, ktora przechowa znaki i ich ilosc wystapien 
		while((line = br.readLine()) != null) { //dopoki mamy co czytac
			String arg[] = line.split(" "); //zczytujemy linie i dzielimy ja na komende i znak
			String command = arg[0]; //pierwsza jest komenda
			char c = arg[1].charAt(0); //drugi znak
			if(command.equalsIgnoreCase("dopisz")) { //nastepnie rozpoznajemy typ komendy
				result = dopisz(result, c);
				int amount = counter.containsKey(c) ? counter.get(c) : 0; //jezeli znak istnieje, pobieramy jego ilosc wystapien z mapy, jezeli nie - ustawiamy zmienna na 0
				counter.put(c, amount+1); //nastepnie dodajemy znak do mapy, zwieksajac jego ilosc wystapien o 1
			}else if(command.equalsIgnoreCase("zmien")) { 
				result = zmien(result, c);
			}else if(command.equalsIgnoreCase("usun")) {
				result = usun(result);
			}
			else if(command.equalsIgnoreCase("przesun")) {
				result = przesun(result, c);
			}
		}
		br.close();
		int max = -1; //na koniec szukamy najczesciej wystepujacego znaku
		char maxC = '0'; 
		for(char c : counter.keySet()) {
			if(counter.get(c) > max) {
				max = counter.get(c);
				maxC = c;
			}
		}
		System.out.println(maxC + " " + max); //zwracamy wynik
	}
	
	static String dopisz(String txt, char c) { //funkcja dopisujaca znak na koncu tekstu
		return txt + c;
	}
	static String zmien(String txt, char c) { //funkcja podmieniajaca ostatni znak
		char[] chars = txt.toCharArray();
		chars[chars.length-1] = c;
		return new String(chars);
	}
	static String usun(String txt) { //funkcja usuwajaca ostatni znak
		return txt.substring(0, txt.length()-1);
	}
	static String przesun(String txt, char c) { //funkcja podmieniajaca pierwsze wystapienie znaku
		int t = txt.indexOf(c);
		if(t == - 1) {
			return txt;
		}
		if(c == 'Z') {
			c = 'A';
		}
		else {
			c++;
		}
		char[] chars = txt.toCharArray();
		chars[t] = c;
		return new String(chars);
	}
}

package matura;

import java.io.BufferedReader;

import java.io.File;

import java.io.FileReader;

import java.io.IOException;

import java.util.HashMap;

public class Podpunkt3 {

public static void main(String[] args) throws IOException {

File f = new File("C:\\DANE_2105\\instrukcje.txt"); //ladujemy plik

BufferedReader br = new BufferedReader(new FileReader(f)); //odczytujemy go za pomoca buffered readera

String line = ""; //zmienna przechowujaca aktualny wiersz

String result = ""; //zmienna przechowujaca wynik

HashMap<Character, Integer> counter = new HashMap<Character, Integer>(); //tworzymy zmienna, ktora przechowa znaki i ich ilosc wystapien

while((line = br.readLine()) != null) { //dopoki mamy co czytac

String arg[] = line.split(" "); //zczytujemy linie i dzielimy ja na komende i znak

String command = arg[0]; //pierwsza jest komenda

char c = arg[1].charAt(0); //drugi znak

if(command.equalsIgnoreCase("dopisz")) { //nastepnie rozpoznajemy typ komendy

result = dopisz(result, c);

int amount = counter.containsKey(c) ? counter.get(c) : 0; //jezeli znak istnieje, pobieramy jego ilosc wystapien z mapy, jezeli nie - ustawiamy zmienna na 0

counter.put(c, amount+1); //nastepnie dodajemy znak do mapy, zwieksajac jego ilosc wystapien o 1

}else if(command.equalsIgnoreCase("zmien")) {

result = zmien(result, c);

}else if(command.equalsIgnoreCase("usun")) {

result = usun(result);

}

else if(command.equalsIgnoreCase("przesun")) {

result = przesun(result, c);

}

br.close();

int max = -1; //na koniec szukamy najczesciej wystepujacego znaku

char maxC = '0';

for(char c : counter.keySet()) {

if(counter.get(c) > max) {

max = counter.get(c);

maxC = c;

}

System.out.println(maxC + " " + max); //zwracamy wynik

}

static String dopisz(String txt, char c) { //funkcja dopisujaca znak na koncu tekstu

return txt + c;

}

static String zmien(String txt, char c) { //funkcja podmieniajaca ostatni znak

char[] chars = txt.toCharArray();

chars[chars.length-1] = c;

return new String(chars);

}

static String usun(String txt) { //funkcja usuwajaca ostatni znak

return txt.substring(0, txt.length()-1);

}

static String przesun(String txt, char c) { //funkcja podmieniajaca pierwsze wystapienie znaku

int t = txt.indexOf(c);

if(t == - 1) {

return txt;

}

if(c == 'Z') {

c = 'A';

}

else {

c++;

}

char[] chars = txt.toCharArray();

chars[t] = c;

return new String(chars);

}

Python

def dopisz(txt, c): #funkcja dopsisujaca znak
    return txt + c


def zmien(txt, c): #funckja zmieniajaca ostatni znak
    txtlist = list(txt) #uwaga: w pythonie teksty musimy potraktowac jako liste
    txtlist[len(txt)-1] = c #jezeli chcemy podmienic znak na danej pozycji
    return "".join(txtlist) #na koniec liste ta musimy zmienic z powrotem na tekst


def usun(txt): #funkcja usuwajaca ostatni znak
    return txt[:len(txt)-1]


def przesun(txt, c): #funkcja przesuwajaca znak o jedno miejsce w tablicy ASCII
    index = txt.find(c)
    if index == -1: #jezeli nie znalezlismy znaku, przerywamy dzialanie
        return txt
    if c == 'Z': #jezeli jest to ostatnia litera alfabetu, to wracamy na poczatek
        c = 'A'
    else: #w przeciwnym przypadku przesuwamy znak o 1
        c = chr(ord(c) + 1)
    txtlist = list(txt) #nastepnie musimy ponownie zamienic text na liste znakow
    txtlist[index] = c #podmienic znak
    return "".join(txtlist) #i zwrocic ja jako ciag znakow


file = open("C:\\DANE_2105\\instrukcje.txt", "r") #otwieramy plik w trybie read
result = "" #zmienna przechowujaca nasz wynik
charMap = {} #tworzymy mapę, która przechowa znaki i ich ilosc wystapien
for line in file: #iterujemy poprzez kazdy wiersz
    args = line.split(" ") #nastepnie dzielimy go na komende i znak
    char = args[1][0]#drugi jest znak
    command = args[0] #pierwsza komenda
    if command == "DOPISZ": #wywolujemy odpowiednie funkcje wg komendy
        result = dopisz(result, char)
        if char in charMap: #jezeli mamy juz dany znak w mapie
            charMap[char] += 1 #to zwiekszamy jego licznik wystapien
        else:
            charMap[char] = 1 #w przeciwnym wypadku dodajemy go do mapy i ustawiamy licznik na 1
    if command == "ZMIEN":
        result = zmien(result, char)
    if command == "USUN":
        result = usun(result)
    if command == "PRZESUN":
        result = przesun(result, char)
file.close() #na koniec musimy zamknac plik
maxlen = -1 #zmienna przechowujaca najwieksza ilosc wystapien
maxC = '0' #zmienna przechwoujaca najczesciej wystepujacy znak
for k in charMap: #nastepnie musimy wyszukac ktory znak byl dopisywany najczesciej
    if charMap[k] > maxlen: #jezeli dany znak wystepowal czesciej niz najczestszy przechowany
        maxC = k #to podmieniamy go
        maxlen = charMap[k] #i ilosc wystapien
print(maxC, " ", maxlen) #drukujemy wynik

def dopisz(txt, c): #funkcja dopsisujaca znak

return txt + c

def zmien(txt, c): #funckja zmieniajaca ostatni znak

txtlist = list(txt) #uwaga: w pythonie teksty musimy potraktowac jako liste

txtlist[len(txt)-1] = c #jezeli chcemy podmienic znak na danej pozycji

return "".join(txtlist) #na koniec liste ta musimy zmienic z powrotem na tekst

def usun(txt): #funkcja usuwajaca ostatni znak

return txt[:len(txt)-1]

def przesun(txt, c): #funkcja przesuwajaca znak o jedno miejsce w tablicy ASCII

index = txt.find(c)

if index == -1: #jezeli nie znalezlismy znaku, przerywamy dzialanie

return txt

if c == 'Z': #jezeli jest to ostatnia litera alfabetu, to wracamy na poczatek

c = 'A'

else: #w przeciwnym przypadku przesuwamy znak o 1

c = chr(ord(c) + 1)

txtlist = list(txt) #nastepnie musimy ponownie zamienic text na liste znakow

txtlist[index] = c #podmienic znak

return "".join(txtlist) #i zwrocic ja jako ciag znakow

file = open("C:\\DANE_2105\\instrukcje.txt", "r") #otwieramy plik w trybie read

result = "" #zmienna przechowujaca nasz wynik

charMap = {} #tworzymy mapę, która przechowa znaki i ich ilosc wystapien

for line in file: #iterujemy poprzez kazdy wiersz

args = line.split(" ") #nastepnie dzielimy go na komende i znak

char = args[1][0]#drugi jest znak

command = args[0] #pierwsza komenda

if command == "DOPISZ": #wywolujemy odpowiednie funkcje wg komendy

result = dopisz(result, char)

if char in charMap: #jezeli mamy juz dany znak w mapie

charMap[char] += 1 #to zwiekszamy jego licznik wystapien

else:

charMap[char] = 1 #w przeciwnym wypadku dodajemy go do mapy i ustawiamy licznik na 1

if command == "ZMIEN":

result = zmien(result, char)

if command == "USUN":

result = usun(result)

if command == "PRZESUN":

result = przesun(result, char)

file.close() #na koniec musimy zamknac plik

maxlen = -1 #zmienna przechowujaca najwieksza ilosc wystapien

maxC = '0' #zmienna przechwoujaca najczesciej wystepujacy znak

for k in charMap: #nastepnie musimy wyszukac ktory znak byl dopisywany najczesciej

if charMap[k] > maxlen: #jezeli dany znak wystepowal czesciej niz najczestszy przechowany

maxC = k #to podmieniamy go

maxlen = charMap[k] #i ilosc wystapien

print(maxC, " ", maxlen) #drukujemy wynik

Odpowiedzią jest litera Z, która dopisywana była 37 razy.

Podpunkt 4

Podpunkt ten mamy już właściwie z głowy – nasza bazowa wersja programu drukuje już gotowy napis po wykonaniu wszystkich funkcji. Dla mniej uważnych poniżej ponownie zamieszczamy implementacje:

C++

#include &lt;iostream>
#include &lt;fstream>

using namespace std;

string dopisz(string text, const char &amp;c){ //funkcja dopisujaca podany znak
    return text + c;
}
string zmien(string text, const char &amp;c){ //funkcja zmieniajaca ostatni znak
    text[text.length()-1] = c;
    return text;
}
string usun(string text){ //funkcja usuwajaca ostatni znak
    text.pop_back();
    return text;
}
string przesun(string text, char &amp;c){ //funkcja przesuwajaca znak
    int t = text.find(c); //najpierw sprawdzamy, czy dany znak w ogole istnieje
    if(t != -1){ //jezeli tak
        if(c == 'Z'){//to najpierw sprawdzamy czy nie jest ostatnia litera alfabetu
            c = 'A'; //jezeli tak, to go przesuwamy
        }
        else{
            c++; //:) w przeciwnym przypadku zwiekszamy go o jeden (kolejny znak w tablicy ASCII)
        }
        text[t] = c; //podmieniamy nastepnie znak
    }
    return text;
}

int main()
{
    fstream input("C:\\dane-2021\\instrukcje.txt", fstream::in); //otwieramy nasz plik
    string napis = ""; //definujemy zmienna przechowujaca finalny napis
    if(!input){
        perror("Nie udalo sie otworzyc pliku");
        return 1;
    }
    string s; //zmienna przechowujaca aktualna komende/znak
    bool isCommand = true; //zmienna informujaca, czy aktualnie mamy doczynienia z komenda czy ze znakiem
    char currentChar = '0'; //zmienna przechowujaca aktualny znak w wierszu
    int command = -1; //zmienna przechowujaca aktualna komende wiersza
    while(input >> s){ //dopoki nie napotkamy konca pliku
        if(isCommand){ //sprawdzamy czy mamy doczynienia z komenda
            if(s == "DOPISZ"){ //jezeli tak to zapisujemy jej kod: 0 - dopisz, 1 - zmien, 2 - usun, 3 - przesun
                command = 0;
            }else if(s == "ZMIEN"){
                command = 1;
            }else if(s == "USUN"){
                command = 2;
            }else if(s == "PRZESUN"){
                command = 3;
            }
            isCommand = false; //przestawiamy zmienna pomocnicza - kolejna zczytana wartosc bedzie znakiem
        }
        else {
            currentChar = s[0]; //pobieramy aktualny znak
            switch(command){ //nastepnie wykonujemy odpowiednia komende wg zapisanego kodu
            case 0:
                napis = dopisz(napis, currentChar);
                break;
            case 1:
                napis = zmien(napis, currentChar);
                break;
            case 2:
                napis = usun(napis);
                break;
            case 3:
                napis = przesun(napis, currentChar);
                break;
            }
            isCommand = true; //przestawiamy zmienna pomocnicza - kolejna zczytana wartosc bedzie komenda
        }
    }
    input.close(); //zawsze należy zamknąć plik, gdy skończymy związane z nim prace
    cout &lt;&lt; napis; //drukujemy finalny napis
    return 0;
}

#include <iostream>

#include <fstream>

using namespace std;

string dopisz(string text, const char &c){ //funkcja dopisujaca podany znak

return text + c;

}

string zmien(string text, const char &c){ //funkcja zmieniajaca ostatni znak

text[text.length()-1] = c;

return text;

}

string usun(string text){ //funkcja usuwajaca ostatni znak

text.pop_back();

return text;

}

string przesun(string text, char &c){ //funkcja przesuwajaca znak

int t = text.find(c); //najpierw sprawdzamy, czy dany znak w ogole istnieje

if(t != -1){ //jezeli tak

if(c == 'Z'){//to najpierw sprawdzamy czy nie jest ostatnia litera alfabetu

c = 'A'; //jezeli tak, to go przesuwamy

}

else{

c++; //:) w przeciwnym przypadku zwiekszamy go o jeden (kolejny znak w tablicy ASCII)

}

text[t] = c; //podmieniamy nastepnie znak

}

return text;

}

int main()

{

fstream input("C:\\dane-2021\\instrukcje.txt", fstream::in); //otwieramy nasz plik

string napis = ""; //definujemy zmienna przechowujaca finalny napis

if(!input){

perror("Nie udalo sie otworzyc pliku");

return 1;

}

string s; //zmienna przechowujaca aktualna komende/znak

bool isCommand = true; //zmienna informujaca, czy aktualnie mamy doczynienia z komenda czy ze znakiem

char currentChar = '0'; //zmienna przechowujaca aktualny znak w wierszu

int command = -1; //zmienna przechowujaca aktualna komende wiersza

while(input >> s){ //dopoki nie napotkamy konca pliku

if(isCommand){ //sprawdzamy czy mamy doczynienia z komenda

if(s == "DOPISZ"){ //jezeli tak to zapisujemy jej kod: 0 - dopisz, 1 - zmien, 2 - usun, 3 - przesun

command = 0;

}else if(s == "ZMIEN"){

command = 1;

}else if(s == "USUN"){

command = 2;

}else if(s == "PRZESUN"){

command = 3;

}

isCommand = false; //przestawiamy zmienna pomocnicza - kolejna zczytana wartosc bedzie znakiem

}

else {

currentChar = s[0]; //pobieramy aktualny znak

switch(command){ //nastepnie wykonujemy odpowiednia komende wg zapisanego kodu

case 0:

napis = dopisz(napis, currentChar);

break;

case 1:

napis = zmien(napis, currentChar);

break;

case 2:

napis = usun(napis);

break;

case 3:

napis = przesun(napis, currentChar);

break;

}

isCommand = true; //przestawiamy zmienna pomocnicza - kolejna zczytana wartosc bedzie komenda

}

input.close(); //zawsze należy zamknąć plik, gdy skończymy związane z nim prace

cout << napis; //drukujemy finalny napis

return 0;

}

Java

package matura;

import java.io.BufferedReader;
import java.io.File;
import java.io.FileReader;
import java.io.IOException;

public class Zadanie4 {

	public static void main(String[] args) throws IOException {
		File f = new File("C:\\DANE_2105\\instrukcje.txt"); //ladujemy plik
		BufferedReader br = new BufferedReader(new FileReader(f)); //odczytujemy go za pomoca buffered readera
		String line = ""; //zmienna przechowujaca aktualny wiersz
		String result = ""; //zmienna przechowujaca wynik
		while((line = br.readLine()) != null) { //dopoki mamy co czytac
			String arg[] = line.split(" "); //zczytujemy linie i dzielimy ja na komende i znak
			String command = arg[0]; //pierwsza jest komenda
			char c = arg[1].charAt(0); //drugi znak
			if(command.equalsIgnoreCase("dopisz")) { //nastepnie rozpoznajemy typ komendy
				result = dopisz(result, c);
			}else if(command.equalsIgnoreCase("zmien")) { 
				result = zmien(result, c);
			}else if(command.equalsIgnoreCase("usun")) {
				result = usun(result);
			}
			else if(command.equalsIgnoreCase("przesun")) {
				result = przesun(result, c);
			}
		}
		br.close();
		System.out.println(result); //zwracamy wynik
	}
	
	static String dopisz(String txt, char c) { //funkcja dopisujaca znak na koncu tekstu
		return txt + c;
	}
	static String zmien(String txt, char c) { //funkcja podmieniajaca ostatni znak
		char[] chars = txt.toCharArray();
		chars[chars.length-1] = c;
		return new String(chars);
	}
	static String usun(String txt) { //funkcja usuwajaca ostatni znak
		return txt.substring(0, txt.length()-1);
	}
	static String przesun(String txt, char c) { //funkcja podmieniajaca pierwsze wystapienie znaku
		int t = txt.indexOf(c);
		if(t == - 1) {
			return txt;
		}
		if(c == 'Z') {
			c = 'A';
		}
		else {
			c++;
		}
		char[] chars = txt.toCharArray();
		chars[t] = c;
		return new String(chars);
	}
}

package matura;

import java.io.BufferedReader;

import java.io.File;

import java.io.FileReader;

import java.io.IOException;

public class Zadanie4 {

public static void main(String[] args) throws IOException {

File f = new File("C:\\DANE_2105\\instrukcje.txt"); //ladujemy plik

BufferedReader br = new BufferedReader(new FileReader(f)); //odczytujemy go za pomoca buffered readera

String line = ""; //zmienna przechowujaca aktualny wiersz

String result = ""; //zmienna przechowujaca wynik

while((line = br.readLine()) != null) { //dopoki mamy co czytac

String arg[] = line.split(" "); //zczytujemy linie i dzielimy ja na komende i znak

String command = arg[0]; //pierwsza jest komenda

char c = arg[1].charAt(0); //drugi znak

if(command.equalsIgnoreCase("dopisz")) { //nastepnie rozpoznajemy typ komendy

result = dopisz(result, c);

}else if(command.equalsIgnoreCase("zmien")) {

result = zmien(result, c);

}else if(command.equalsIgnoreCase("usun")) {

result = usun(result);

}

else if(command.equalsIgnoreCase("przesun")) {

result = przesun(result, c);

}

br.close();

System.out.println(result); //zwracamy wynik

}

static String dopisz(String txt, char c) { //funkcja dopisujaca znak na koncu tekstu

return txt + c;

}

static String zmien(String txt, char c) { //funkcja podmieniajaca ostatni znak

char[] chars = txt.toCharArray();

chars[chars.length-1] = c;

return new String(chars);

}

static String usun(String txt) { //funkcja usuwajaca ostatni znak

return txt.substring(0, txt.length()-1);

}

static String przesun(String txt, char c) { //funkcja podmieniajaca pierwsze wystapienie znaku

int t = txt.indexOf(c);

if(t == - 1) {

return txt;

}

if(c == 'Z') {

c = 'A';

}

else {

c++;

}

char[] chars = txt.toCharArray();

chars[t] = c;

return new String(chars);

}

Python

def dopisz(txt, c): #funkcja dopsisujaca znak
    return txt + c


def zmien(txt, c): #funckja zmieniajaca ostatni znak
    txtlist = list(txt) #uwaga: w pythonie teksty musimy potraktowac jako liste
    txtlist[len(txt)-1] = c #jezeli chcemy podmienic znak na danej pozycji
    return "".join(txtlist) #na koniec liste ta musimy zmienic z powrotem na tekst


def usun(txt): #funkcja usuwajaca ostatni znak
    return txt[:len(txt)-1]


def przesun(txt, c): #funkcja przesuwajaca znak o jedno miejsce w tablicy ASCII
    index = txt.find(c)
    if index == -1: #jezeli nie znalezlismy znaku, przerywamy dzialanie
        return txt
    if c == 'Z': #jezeli jest to ostatnia litera alfabetu, to wracamy na poczatek
        c = 'A'
    else: #w przeciwnym przypadku przesuwamy znak o 1
        c = chr(ord(c) + 1)
    txtlist = list(txt) #nastepnie musimy ponownie zamienic text na liste znakow
    txtlist[index] = c #podmienic znak
    return "".join(txtlist) #i zwrocic ja jako ciag znakow


file = open("C:\\DANE_2105\\instrukcje.txt", "r") #otwieramy plik w trybie read
result = "" #zmienna przechowujaca nasz wynik
for line in file: #iterujemy poprzez kazdy wiersz
    args = line.split(" ") #nastepnie dzielimy go na komende i znak
    char = args[1][0]#drugi jest znak
    command = args[0] #pierwsza komenda
    if command == "DOPISZ": #wywolujemy odpowiednie funkcje wg komendy
        result = dopisz(result, char)
    if command == "ZMIEN":
        result = zmien(result, char)
    if command == "USUN":
        result = usun(result)
    if command == "PRZESUN":
        result = przesun(result, char)
file.close() #na koniec musimy zamknac plik
print(result) #drukujemy wynik

def dopisz(txt, c): #funkcja dopsisujaca znak

return txt + c

def zmien(txt, c): #funckja zmieniajaca ostatni znak

txtlist = list(txt) #uwaga: w pythonie teksty musimy potraktowac jako liste

txtlist[len(txt)-1] = c #jezeli chcemy podmienic znak na danej pozycji

return "".join(txtlist) #na koniec liste ta musimy zmienic z powrotem na tekst

def usun(txt): #funkcja usuwajaca ostatni znak

return txt[:len(txt)-1]

def przesun(txt, c): #funkcja przesuwajaca znak o jedno miejsce w tablicy ASCII

index = txt.find(c)

if index == -1: #jezeli nie znalezlismy znaku, przerywamy dzialanie

return txt

if c == 'Z': #jezeli jest to ostatnia litera alfabetu, to wracamy na poczatek

c = 'A'

else: #w przeciwnym przypadku przesuwamy znak o 1

c = chr(ord(c) + 1)

txtlist = list(txt) #nastepnie musimy ponownie zamienic text na liste znakow

txtlist[index] = c #podmienic znak

return "".join(txtlist) #i zwrocic ja jako ciag znakow

file = open("C:\\DANE_2105\\instrukcje.txt", "r") #otwieramy plik w trybie read

result = "" #zmienna przechowujaca nasz wynik

for line in file: #iterujemy poprzez kazdy wiersz

args = line.split(" ") #nastepnie dzielimy go na komende i znak

char = args[1][0]#drugi jest znak

command = args[0] #pierwsza komenda

if command == "DOPISZ": #wywolujemy odpowiednie funkcje wg komendy

result = dopisz(result, char)

if command == "ZMIEN":

result = zmien(result, char)

if command == "USUN":

result = usun(result)

if command == "PRZESUN":

result = przesun(result, char)

file.close() #na koniec musimy zamknac plik

print(result) #drukujemy wynik

Odpowiedzią jest napis: POZNIEJMOWIONOZECZLOWIEKTENNADSZEDLODPOLNOCYODBRAMYPOWROZNICZEJSZEDLPIESZOAOBJUCZONEGOKONIAPROWADZILZAUZDEBYLOPOZNEPOPOLUDNIEIKRAMYPOWROZNIKOWIRYMARZYBYLYJUZZAMKNIETEAULICZKAPUSTABYLOCIEPLOACZLOWIEKTENMIALNASOBIECZARNYPLASZCZNARZUCONYNARAMIONAZWRACALUWAGEZATRZYMALSIEPRZEDGOSPODASTARYNARAKORTPOSTALCHWILEPOSLUCHALGWARUGLOSOWGOSPODAJAKZWYKLEOTEJPORZEBYLAPELNALUDZINIEZNAJOMYNIEWSZEDLDOSTAREGONARAKORTUPOCIAGNALKONIADALEJWDOLULICZKITAMBYLADRUGAKARCZMAMNIEJSZANAZYWALASIEPODLISEMTUBYLOPUSTOKARCZMANIEMIALANAJLEPSZEJSLAWY

Wygląda to na tekst z Wiedźmina. Widok spójnego, logicznego tekstu zapewne ucieszył niejednego maturzystę 🙂

Matura z informatyki 2021 zadanie 5 – wodociągi

W zadaniu tym do czynienia mamy ze zbiorem informacji na temat zużycia wody dla każdego domu. Do analizy tego typu informacji najlepiej sprawdzi się Microsoft Excel. Zanim jednak będziemy mogli przejść do rozwiązywania zadania, musimy najpierw pobrać dane z pliku:

Z zakładki Dane wybieramy Z tekstu, a następnie wybieramy plik wodociągi.txt.
Następnie klikamy dalej.
W kolejnym okienku wybieramy rozdzielanie danych za pomocą średnika.
W ostatnim oknie wystarczy już tylko kliknąć Zakończ, a następnie wybrać miejsce, w którym mają się pojawić dane.

Podpunkt 1

Pierwszym krokiem w rozwiązywaniu tego podpunktu będzie stworzenie kolumny, która wyodrębni numer klienta z jego kodu za pomocą funkcji LEWY:

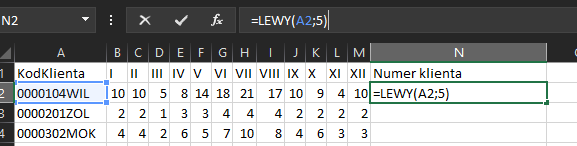
Formułę tę należy oczywiście zastosować dla całej kolumny (zrobisz to klikając szybko dwa razy mały kwadracik w prawym dolnym rogu). Kolejna kolumna będzie wyodrębniała ilość mieszkańców danego klienta z kodu. Skorzystamy z funkcji FRAGMENT.TEKSTU, która pozwala wyciąć określoną ilość znaków z podanego tekstu, zaczynając od wskazanej pozycji:

W kolejnej kolumnie obliczymy ilość wody na jednego mieszkańca – wystarczy w tym celu zsumować zużycie ze wszystkich miesięcy za pomocą SUMA, a następnie podzielić tą wartość przez ilość mieszkańców:

Następnie wystarczy już tylko posortować malejąco dane wg nowoutworzonej kolumny, a następnie wybrać pierwsze 10 wierszy:

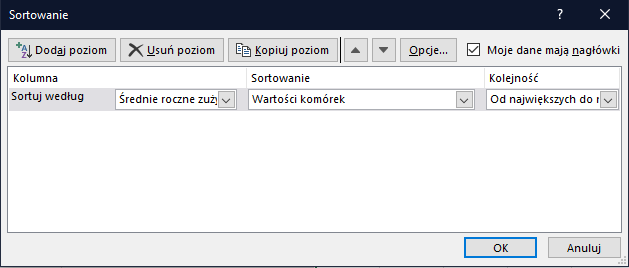
Wybieramy pierwsze 10 rekordów:

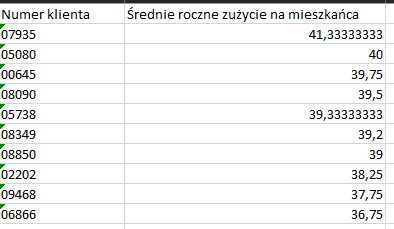
Podpunkt 2

W podpunkcie tym skorzystamy z sumy częściowej. Najpierw jednak musimy stworzyć kolumnę, która wybierze symbol dzielnicy z kodu klienta – tym razem skorzystamy z funkcji PRAWY:

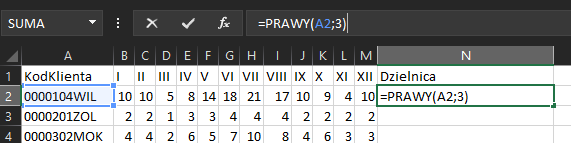
Dla każdego klienta policzymy jeszcze roczne zużycie, aby móc potem je wykorzystać w sumie częściowej:

Po zastosowaniu formuł do całych kolumn musimy jeszcze posortować dane wg dzielnic:

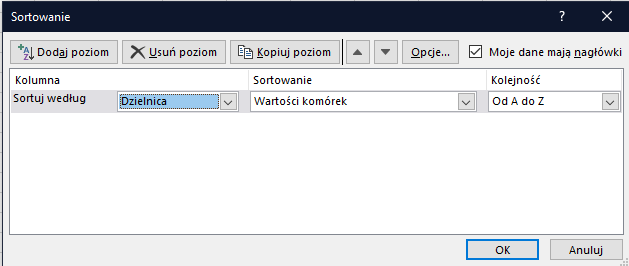
Następnie możemy przejść do obliczania sumy częściowej. Sumę częściową znajdziesz w zakładce Dane w prawym górnym rogu. Dla każdej dzielnicy sumujemy roczne użycie każdego z klientów:

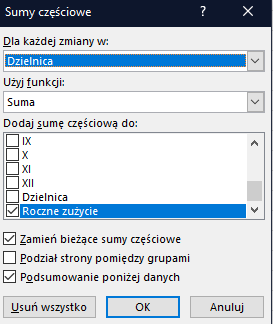
Gdy wyświetlą się wyniki możecie kliknąć Ukryj szczegóły w tym samym panelu co Suma częściowa. Przekopiujmy wyniki do nowego arkusza. Aby jednak prawidłowo skopiować wynik, musicie najpierw zaznaczyć dane, potem przejść do Narzędzia główne, a następnie Znajdź i zaznacz > przejdź do – specjalne… i w okienku wybrać Tylko widoczne komórki:

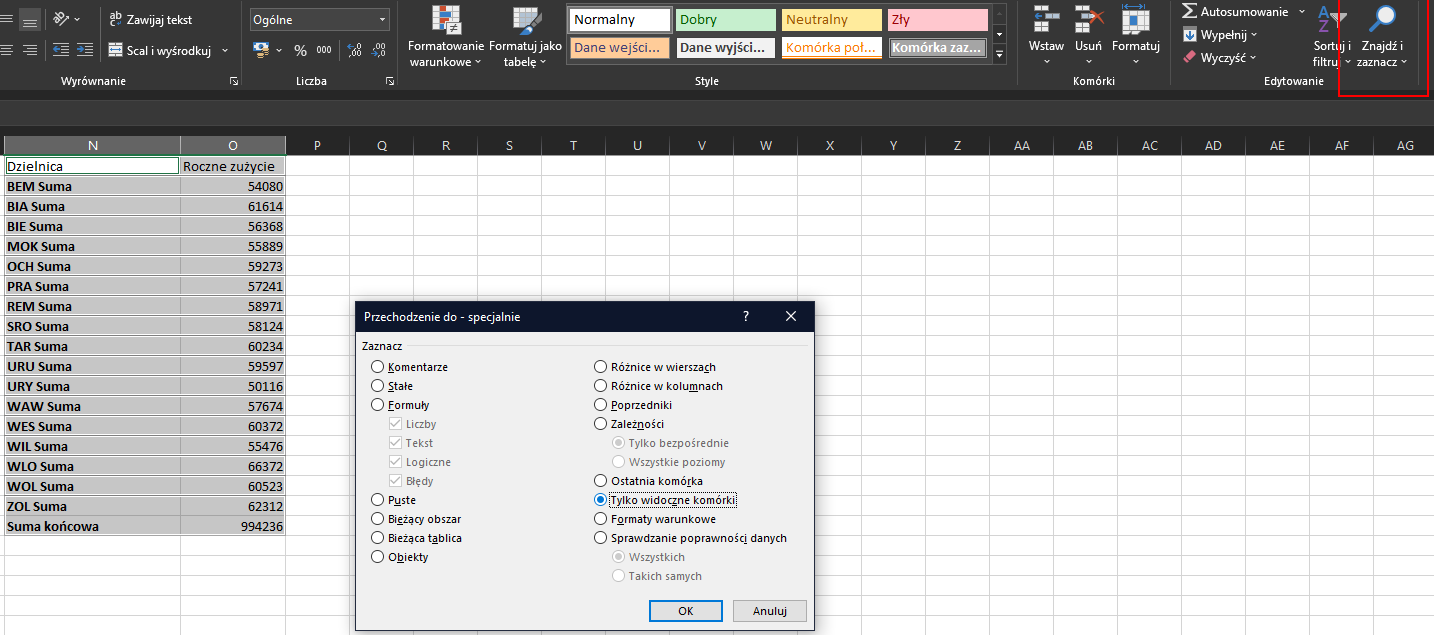
Odpowiedzią jest poniższe zestawienie:

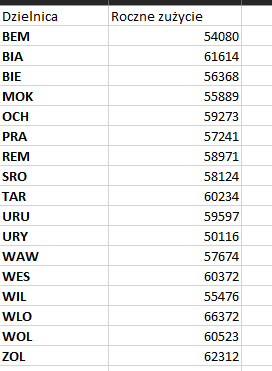
Podpunkt 3

W tym podpunkcie również skorzystamy z sumy częściowej, a także z uprzednio utworzonej kolumny Dzielnica. Przed uruchomieniem sumy częściowej upewnijcie się, że dane są posortowane wg dzielnicy. W podpunkcie tym sumę częściową obliczamy po prostu dla każdego miesiąca, zamiast dla rocznego zużycia. Okienko sumy częściowej powinno wyglądać mniej więcej tak:

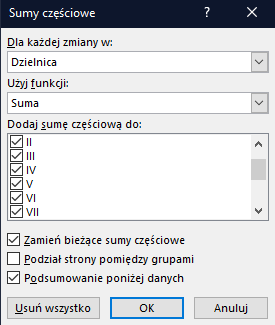
Pamiętajcie o przekopiowaniu danych do arkusza. Odpowiedź prezentuje się następująco:

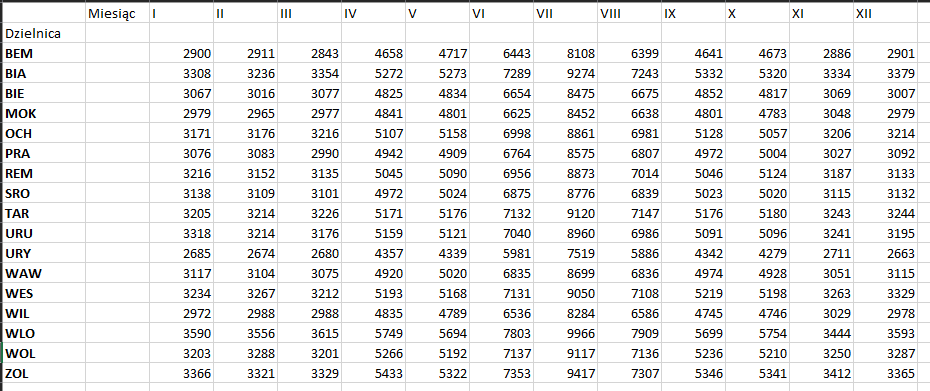
Podpunkt 4

Podpunkt ten, z pozoru skomplikowany, jest tak naprawdę prosty w rozwiązaniu. Najpierw należy zsumować zużycie dla każdego z miesięcy z podanych przez CKE danych:

Następnie dane te możemy przekopiować do nowego arkusza, w którym utworzymy zestawienie zużycia wody na miesiąc dla każdego z lat:

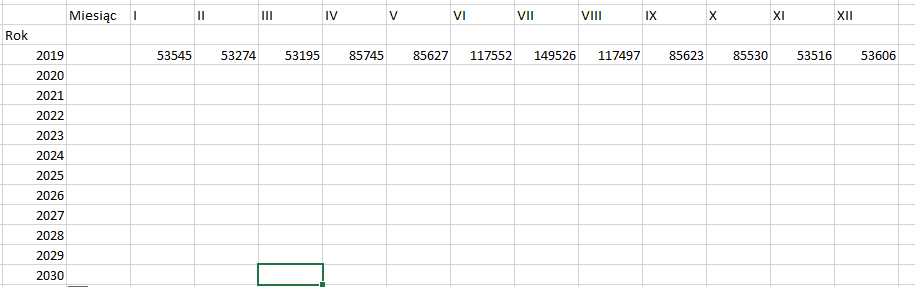
Ilość zużycia wody będzie bazowała na zeszłorocznym zużyciu. Należy pamiętać o zaokrągleniu wartości w górę do liczby całkowitej. Po zastosowaniu formuły dla całej tabeli wyszukamy miesiąc i rok, w którym wartość zużycia przekroczy 160000 metrów sześciennych:

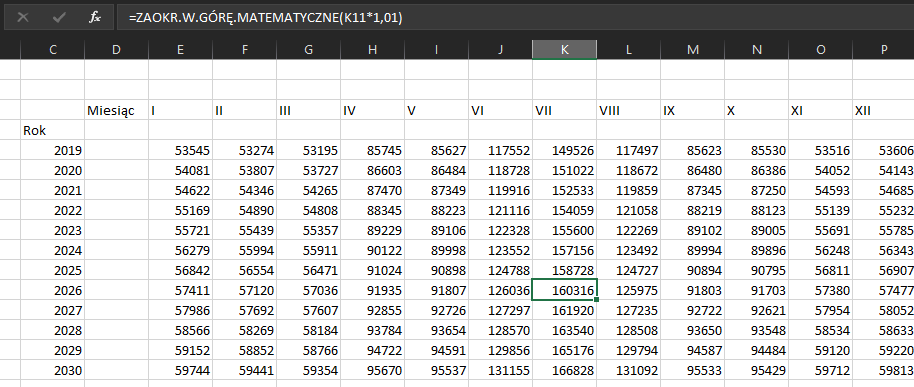
Z zestawienia widzimy, że pierwszy deficyt przepustowości nastąpi w lipcu 2026 roku. Pozostało nam już tylko stworzenie wykresu liniowego dla roku 2030:

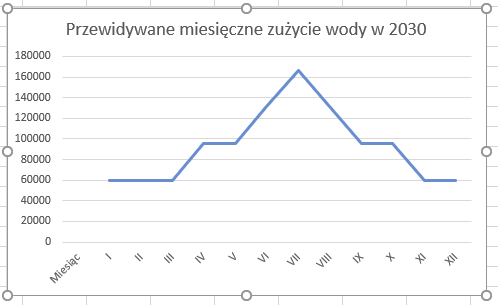
Podpunkt 5

Podpunkt ten jest tak naprawdę uzupełnieniem poprzedniego. Jedyne co musimy zrobić, to stworzyć dodatkową kolumnę przy zestawieniu, która dla każdego roku określi przepustowość sieci wodociągowej. Począwszy od 2021 roku będzie ona rosła o 1000 co roku:

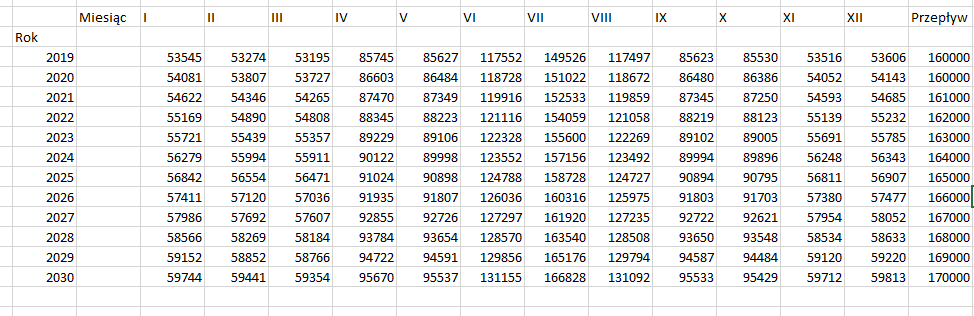
Jak widzimy, do roku 2030 nie nastąpi żaden deficyt, dlatego należy rozszerzyć nasze zestawienie, aż w końcu znajdziemy rok i miesiąc:

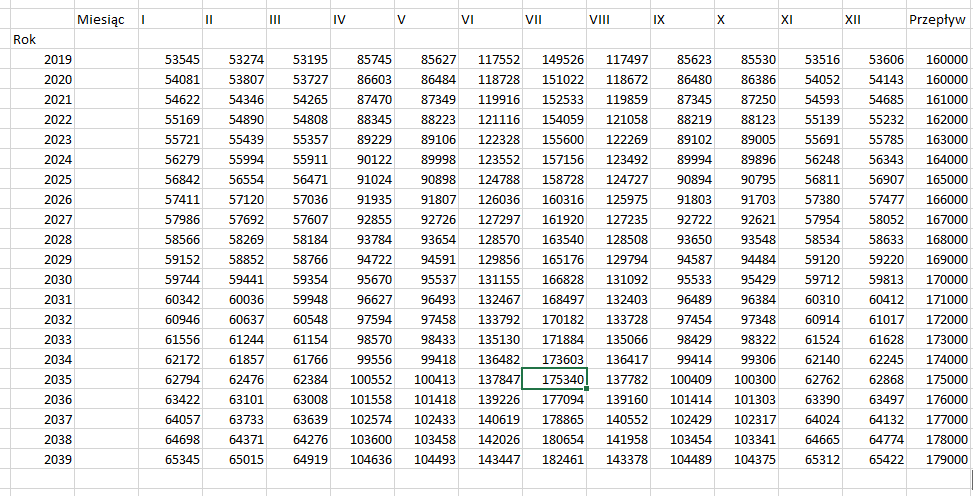
Po rozszerzeniu okaże się, że deficyt ten nastąpi po raz pierwszy w lipcu 2035 roku.

Polecamy również tą książkę, która z pewnością przyda Ci się w dalszej edukacji

Matura z informatyki 2021 zadanie 6 – bitwa

W zadaniu mamy trzy różne pliki z danymi, przez co od razu nasuwa się użycie programu do zarządzania baz danych. Skorzystamy z programu Microsoft Access. Przejdźmy najpierw do importu danych.

Dane importujemy wchodząc w Dane>Nowe źródło danych

Następnie wybieramy plik z danymi. Uwaga: kolejność importowanych danych może mieć znaczenie. Zacznijmy od pliku gracze.txt:

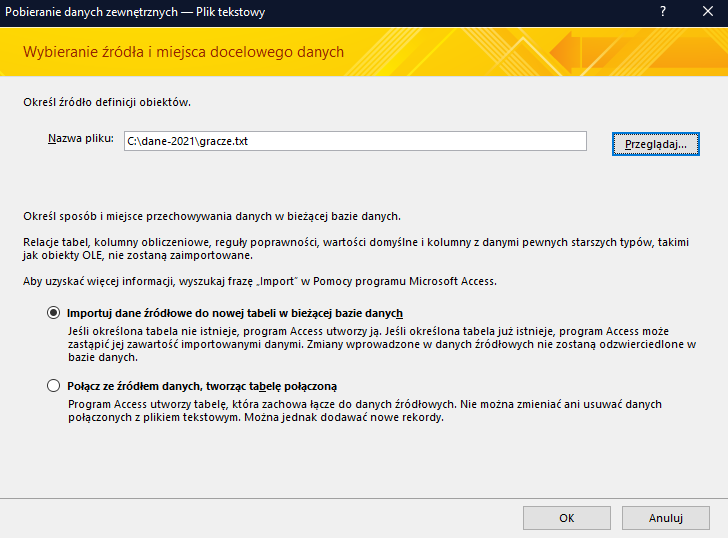
W pierwszych dwóch oknach nic nie zmieniamy.

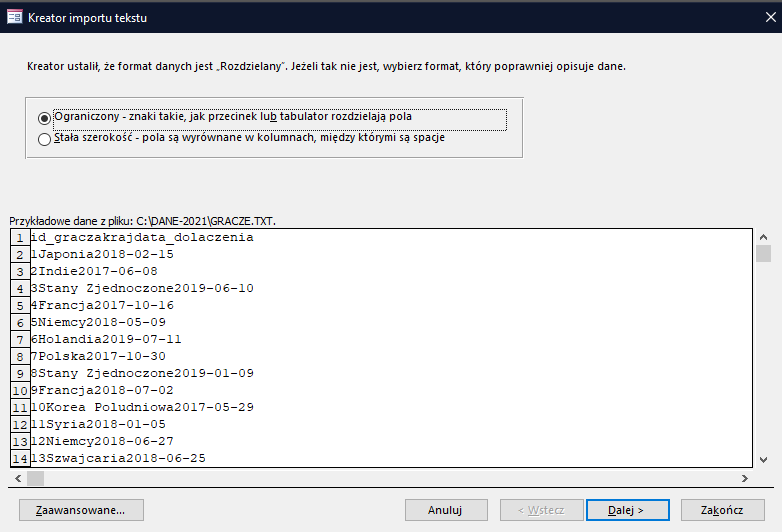
Rozdzielając dane należy wskazać, że pierwszy wiersz zawiera nazwy pól:

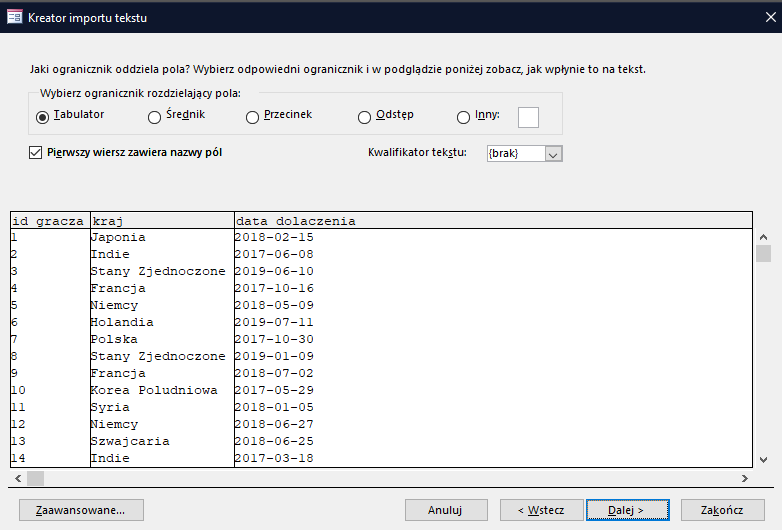
Aby dane zostały zaimportowane prawidłowo trzeba wskazać format daty zgodny z podanym w pliku. W tym celu kliknij Zaawansowane, a następnie wybierz format RMD:

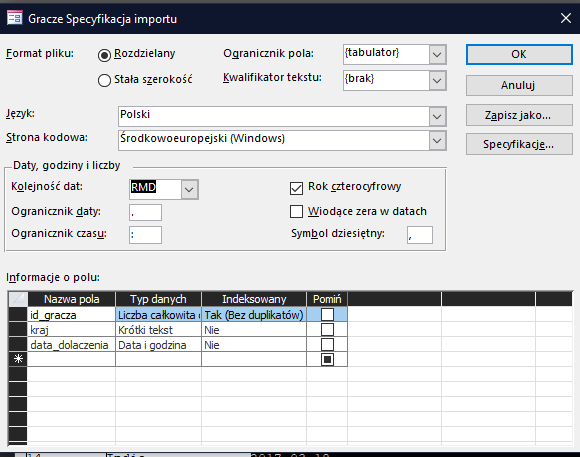
W następnym oknie wybieramy id_gracza jako indeksowany bez duplikatów. Kolejne okno wybieramy to pole jako klucz podstawowy:

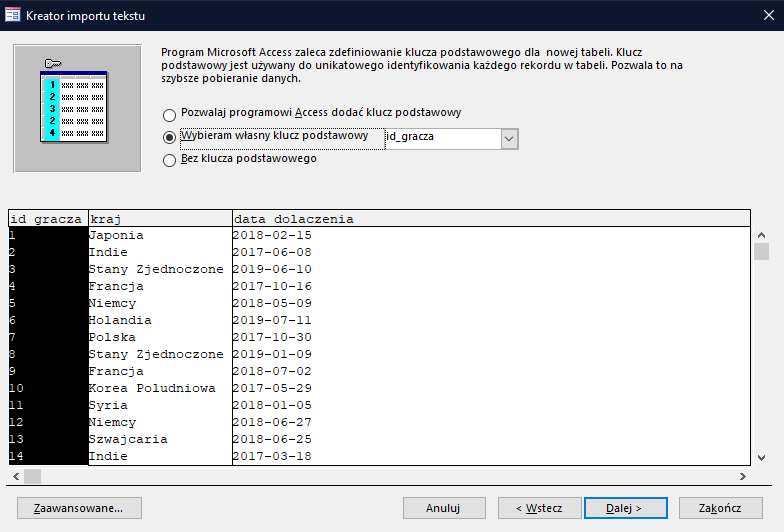
Następnie możesz kliknąć zakończ. Dla pozostałych plików proces wygląda prawie tak samo, z tą różnicą, że dla pól, których nazwy pojawiły się już w pozostałych tabelach należy wybrać indeksowanie z duplikatami:

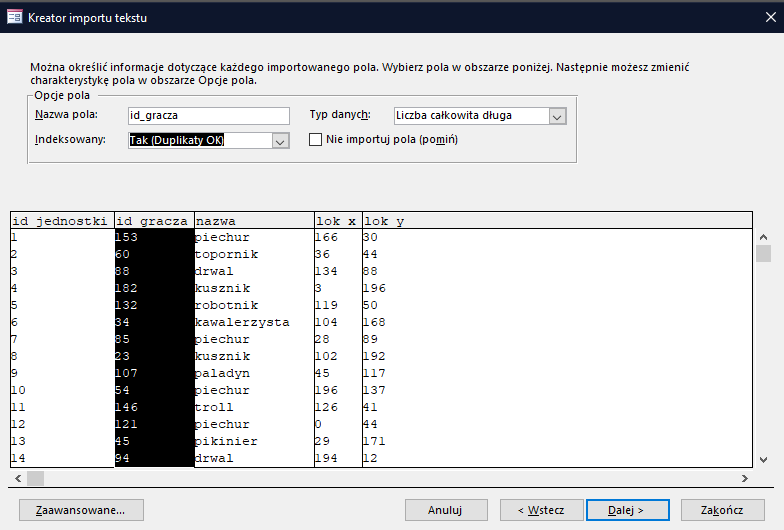
Pamiętajcie też, że pole nazwa również jest indeksowane, a także jest kluczem podstawowym w tabeli klasy.

Gdy zaimportujecie wszystkie dane pozostało już tylko połączyć je relacjami:

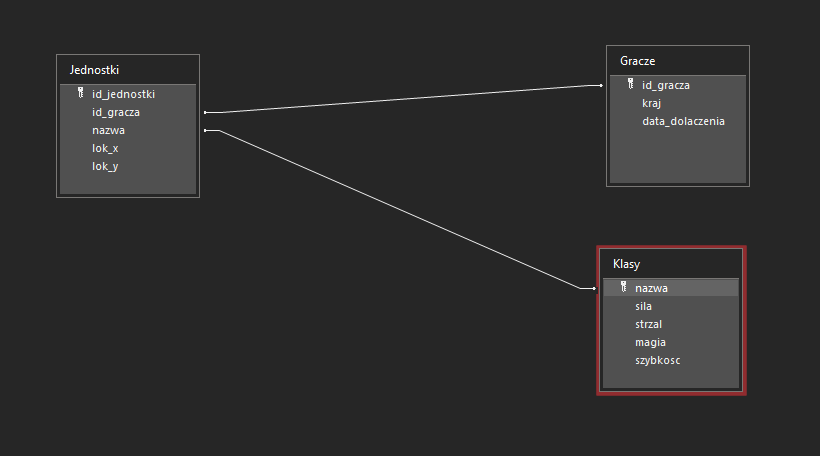
Mając wszystkie tabele możemy przystąpić do rozwiązywania zadania.

Podpunkt 1

W kwerendzie tej skorzystamy z funkcji Year, która zwraca rok z podanej daty. Musimy ustawić kryterium, że rok ten jest równy 2018. Następnie pogrupujemy dane wg kraju, a następnie dla każdego z nich policzymy id_gracza. Ostatnim krokiem jest posortowanie danych malejąco i ograniczenie ilości wyników do pięciu:

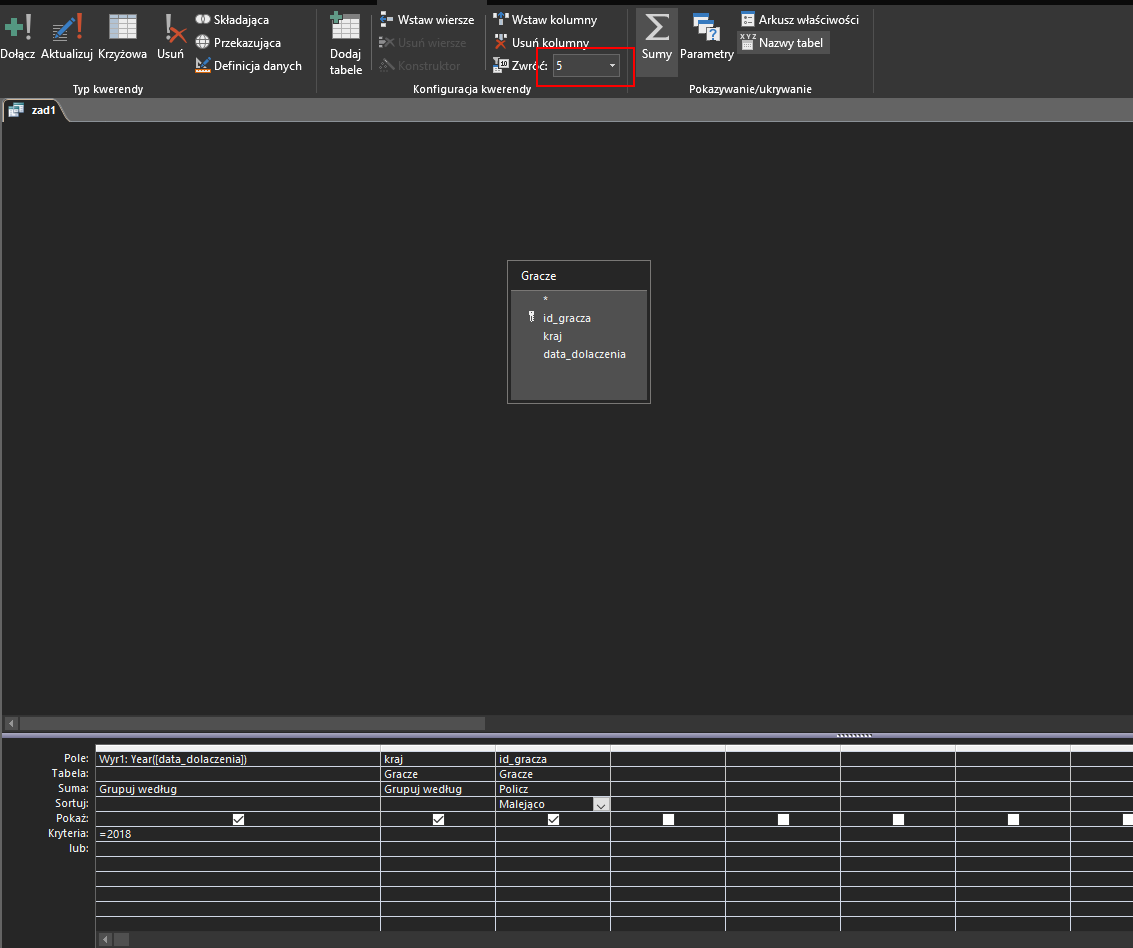
Kwerenda ta generuje nam odpowiedź:

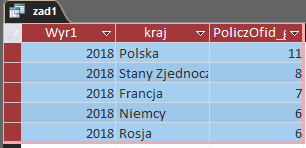
Podpunkt 2

Wykorzystamy prostą kwerendę, która wybiera pola za pomocą Like ‘*elf’, a następnie zsumujemy wartość pola strzal, za pomocą funkcji agregującej:

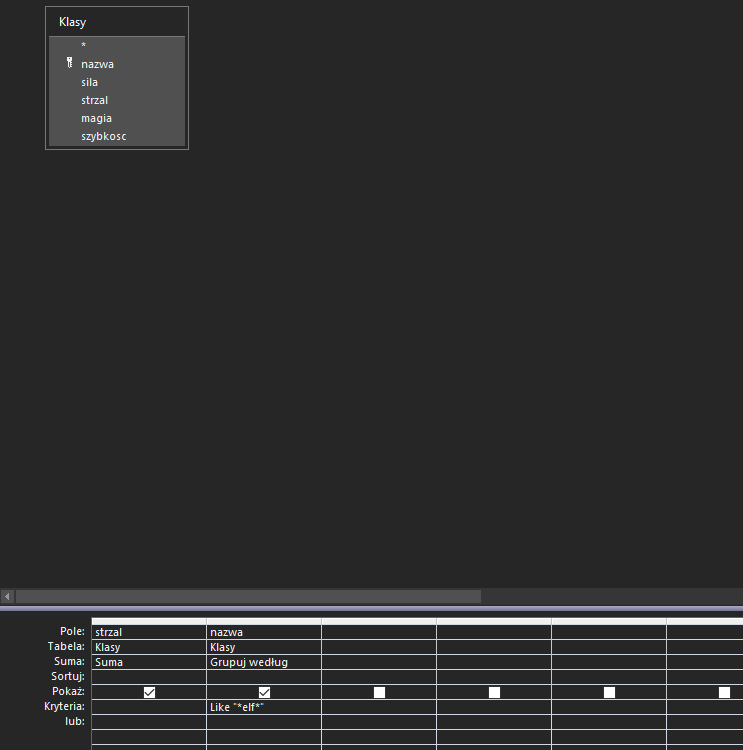
Jak widzicie kwerenda bardzo prosta, a 2 punkty to już 4% z całego egzaminu – prezent od CKE

Odpowiedź wygląda następująco:

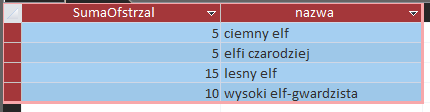
Podpunkt 3

W podpunkcie tym skorzystamy z kwerendy pomocniczej, która wybierze id graczy posiadających podane jednostki. Tak wygląda kwerenda pomocnicza:

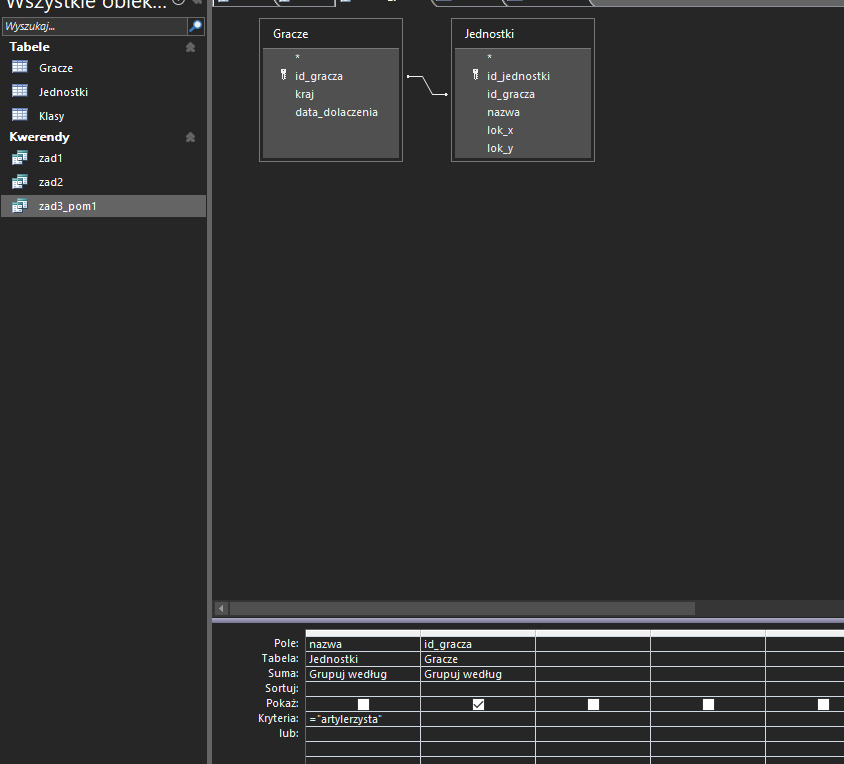
Następnie tworzymy finalną kwerendę, która wybierze te wyniki z tabeli gracze, które nie występują w kwerendzie pomocniczej:

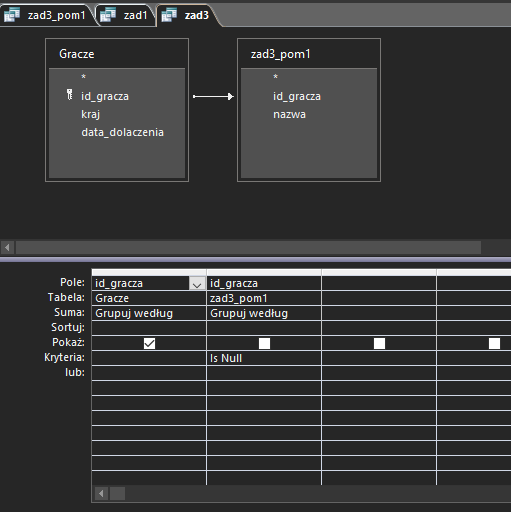
Zwróćcie uwagę, że w relacji strzałka wskazuje na kwerendę pomocniczą, gdzie domyślnie takiej strzałki nie ma. Aby uzyskać taki efekt, należy dwa razy szybko kliknąć w linię relacji, po czym w okienku, które wyskoczyło, wybrać drugą opcję:

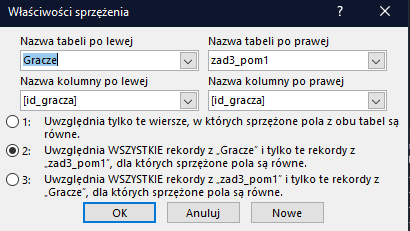
Po uruchomieniu finalna kwerenda generuje odpowiedź:

Podpunkt 4

Nieco bardziej złożony podpunkt, który będzie wymagał użycia dwóch pomocniczych kwerend. W pierwszej z nich obliczymy odległość każdej z jednostek od punktu (100, 100). Wykorzystamy tu funkcję Abs, która zwraca wartość bezwzględną z argumentu:

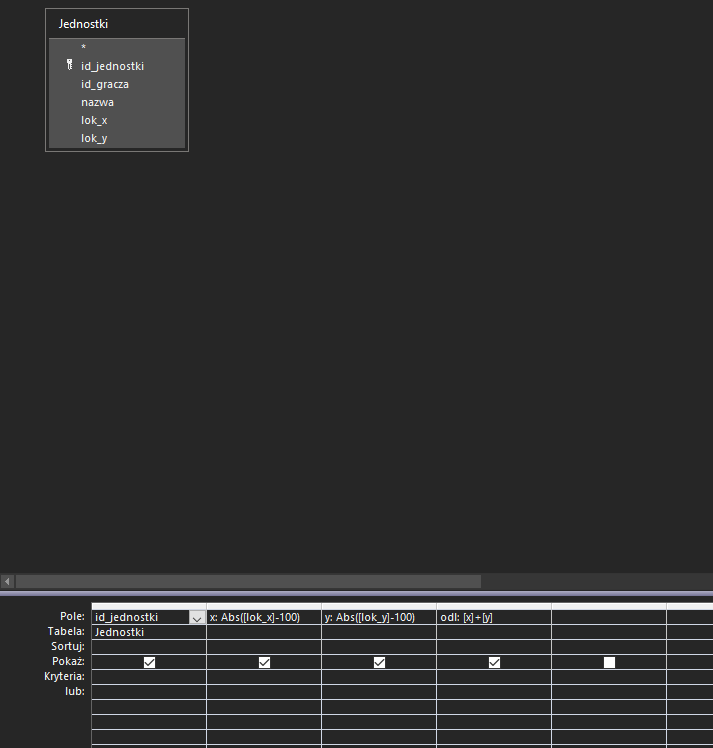
W następnej kwerendzie wybierzemy jednostki, których odległość od tego punktu jest mniejsza lub równa ich szybkości:

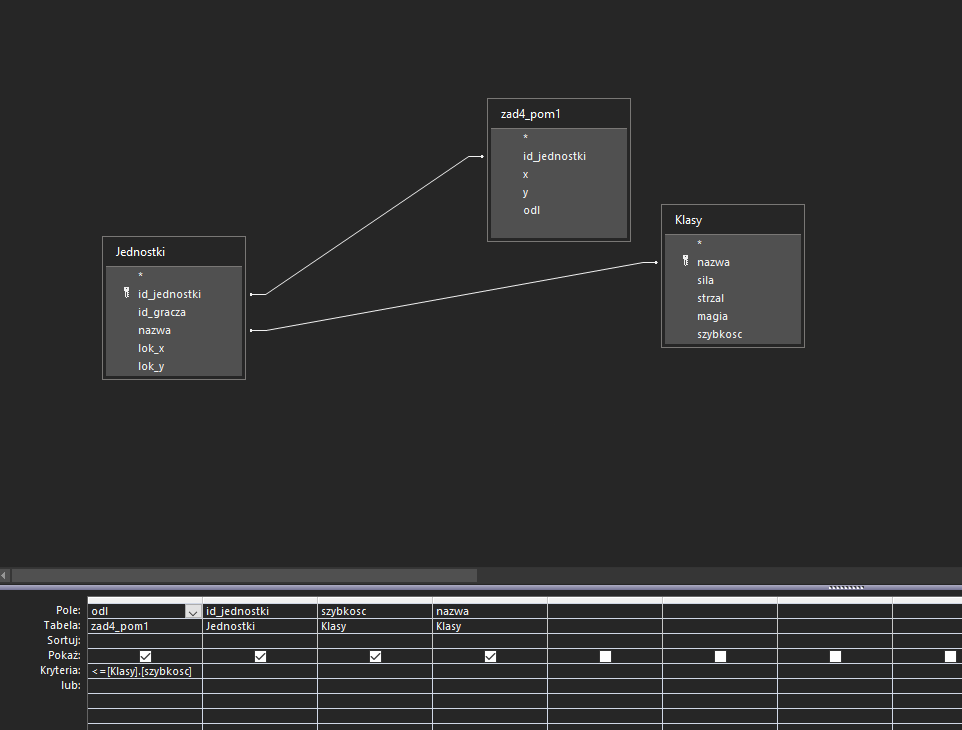
W ostatniej kwerendzie pogrupujemy wyniki wg klasy, a także zliczymy dla każdego typu jednostki, które mogą dojść do tego punktu w jednej turze:

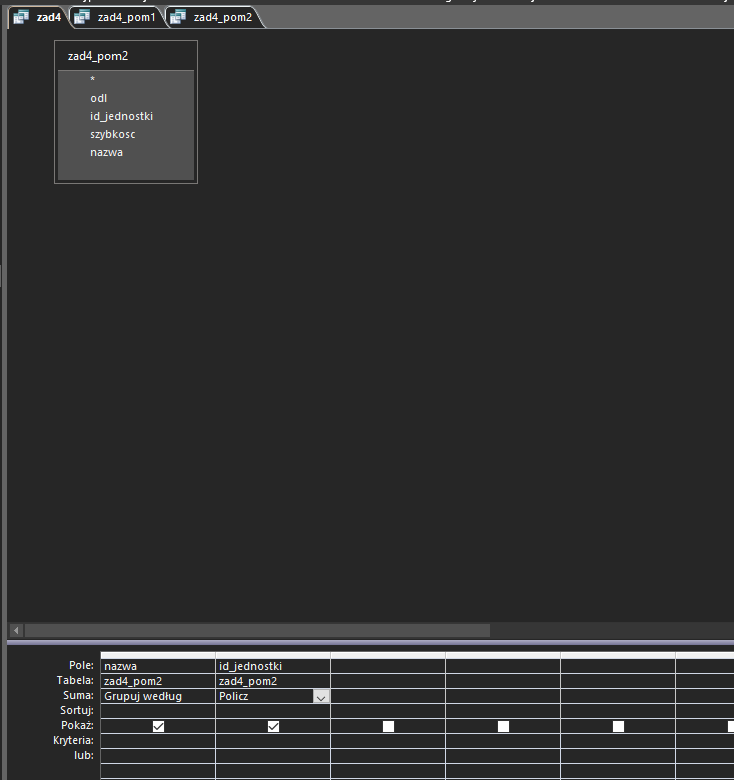
Finalna kwerenda daje nam odpowiedź:

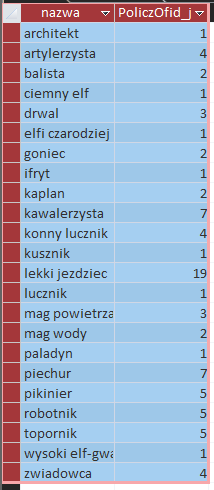
Podpunkt 5

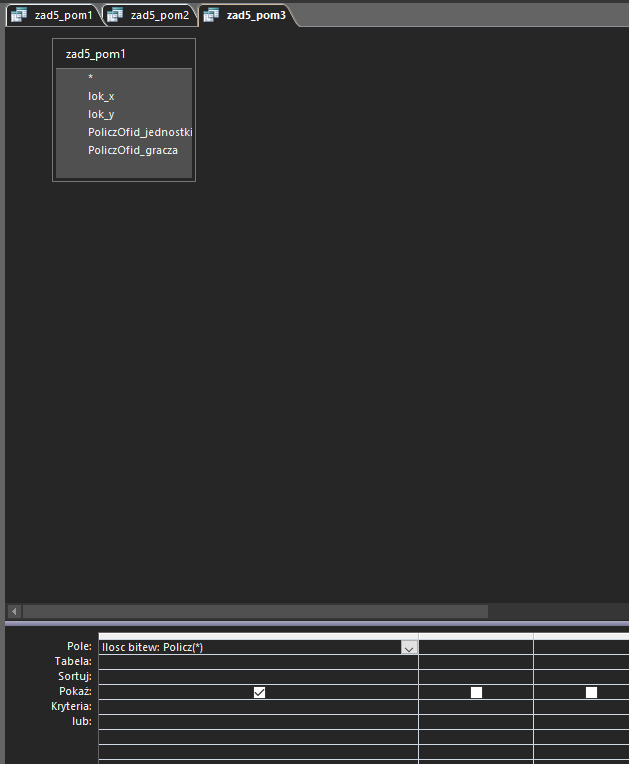
Ostatni podpunkt tej matury będzie wymagał aż czterech kwerend pomocniczych. W pierwszej pogrupujemy dane według pozycji (x i y), a następnie wybierzemy tylko te pozycje, na których znajduje się więcej niż jeden gracz.

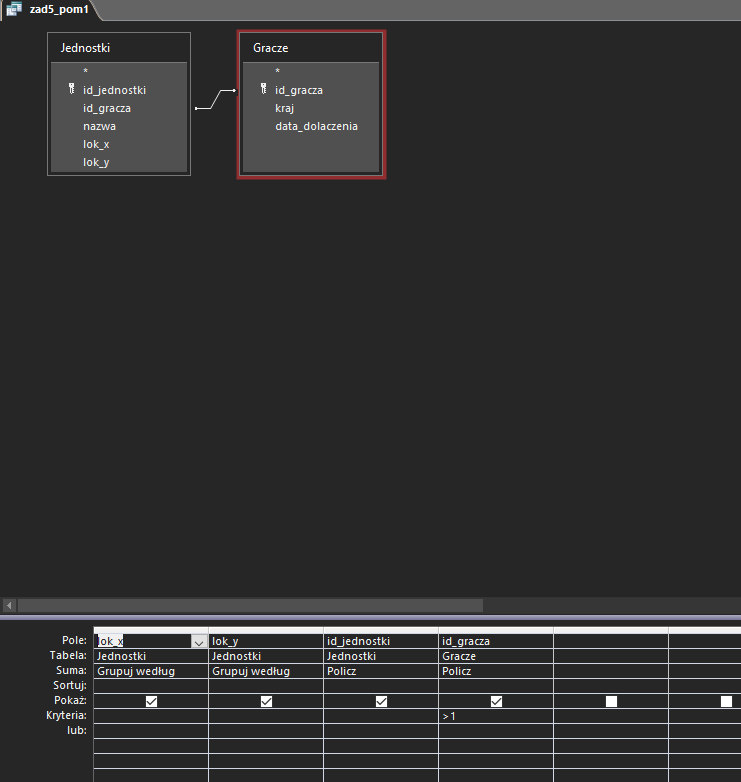
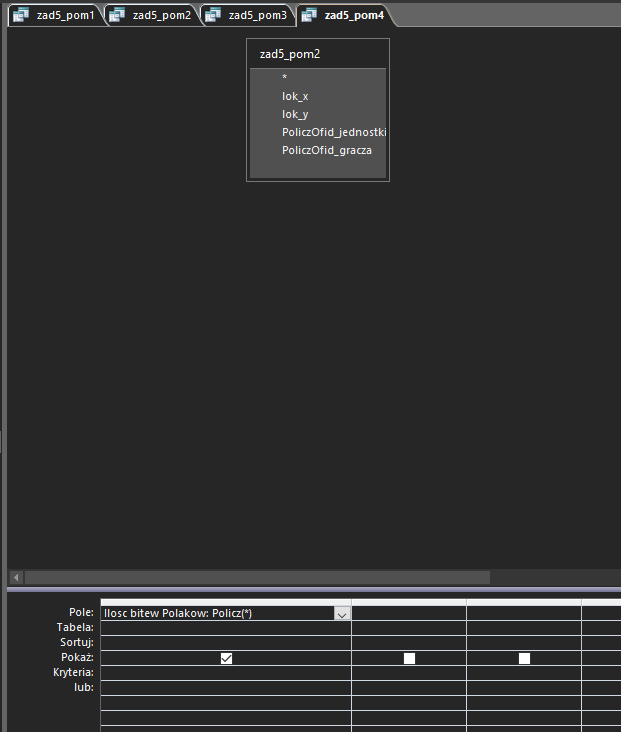
Druga kwerenda wykona dokładnie to samo, z tą różnicą, ze wybierze jedynie graczy z Polski:

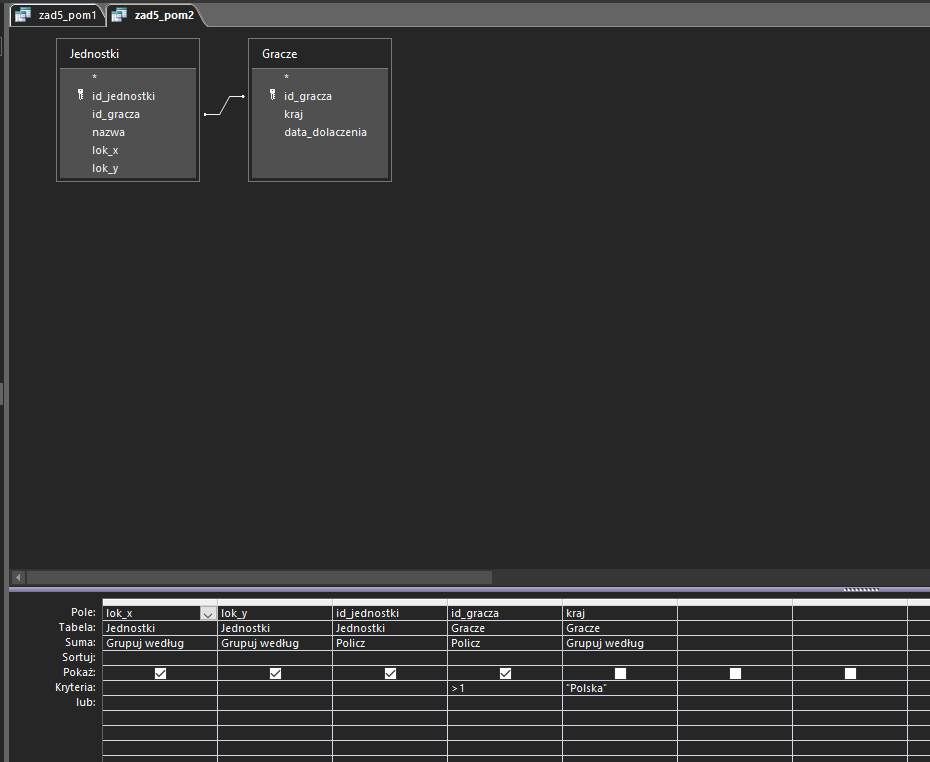
Pozostałe dwie pomocnicze kwerendy zliczą ilość wyników(bitew) z dwóch poprzednich kwerend pomocniczych:

Ostatnia kwerenda, która da nam odpowiedź po prostu zestawi powyższe wyniki:

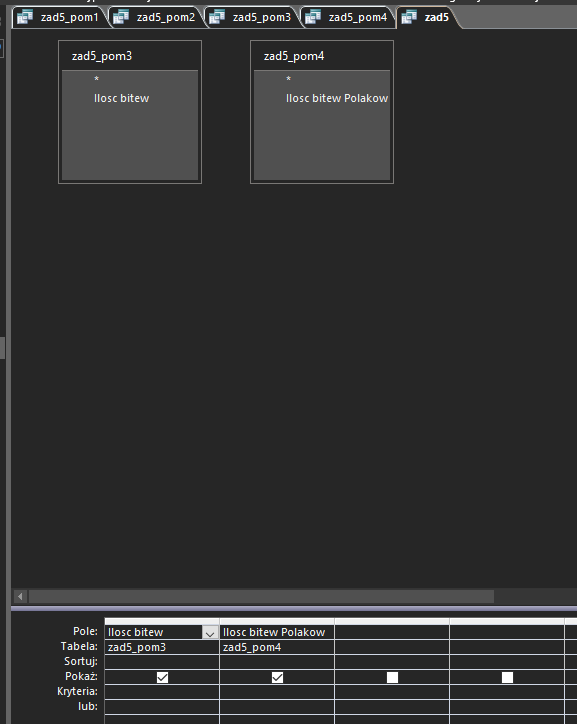
Daje nam to poniższą odpowiedź:

Podsumowanie

Jak sami widzicie matura z informatyki 2021 była znacznie łatwiejsza, niż zeszłoroczne egzaminy. Mamy nadzieję, że większość z Was uzyskała wysokie wyniki. Jeżeli chcecie dalej rozwijać swoje umiejętności, to dobrym pomysłem jest rozpoczęcie nauki języka programowania. Sprawdźcie nasz wpis, w którym przyglądamy się bliżej jednemu z kursów programowania online.

Matura z informatyki 2021 rozwiązania C++, Java, Python

Matura z informatyki 2021 – część pierwsza

Matura z informatyki 2021 zadanie 1 – cyfrowe dopełnienie

Podpunkt 1

Podpunkt 2

Matura z informatyki 2021 zadanie 2 – analiza algorytmu

Podpunkt 1

Podpunkt 2

Podpunkt 3

Matura z informatyki 2021 zadanie 3 – zadania zamknięte

Podpunkt 1

Podpunkt 2

Podpunkt 3

Matura z informatyki 2021 – część druga

Matura z informatyki 2021 zadanie 4 – neon cyfrowy

C++

Java

Python

Podpunkt 1

Podpunkt 2

C++

Java

Python

Podpunkt 3

C++

Java

Python

Podpunkt 4

C++

Java

Python

Matura z informatyki 2021 zadanie 5 – wodociągi

Podpunkt 1

Podpunkt 2

Podpunkt 4

Podpunkt 5

Matura z informatyki 2021 zadanie 6 – bitwa

Podpunkt 1

Podpunkt 2

Podpunkt 3

Podpunkt 4

Podpunkt 5

Podsumowanie

You Might Also Like

Jak wyjść z Vim

Praktyki w Scythe Studio

Praca zdalna jako junior

1 Comment

sattik

Dodaj komentarz Anuluj pisanie odpowiedzi